Содержание
- 2. Монотонность Асимптота Точность Единица Максимум Аргумент Точка Исследование Корень Абсцисса Концентрация внимания
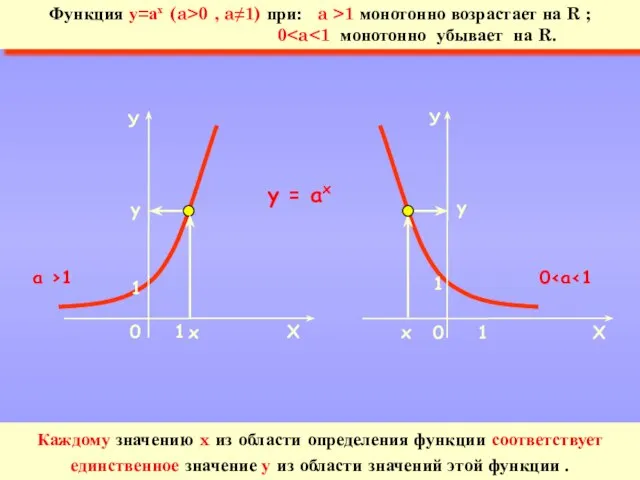
- 3. y = аx х у у 0 х Функция у=ах (a>0 , a≠1) при: a >1
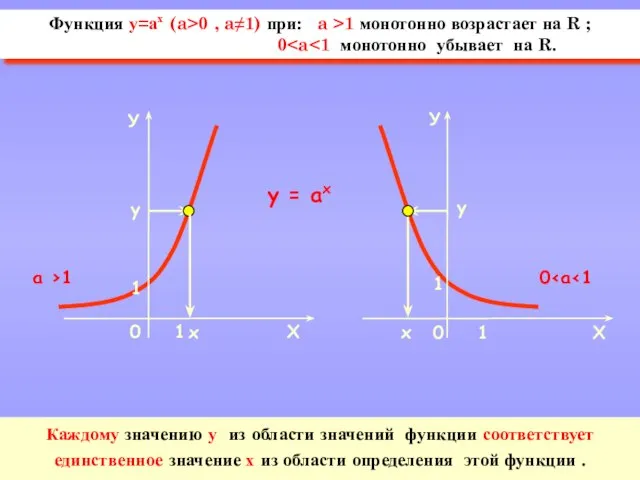
- 4. y = аx х у у 0 х Функция у=ах (a>0 , a≠1) при: a >1
- 5. Функцию y = logax ( а > 0, а ≠ 1 ) называют логарифмической функцией. Определение:
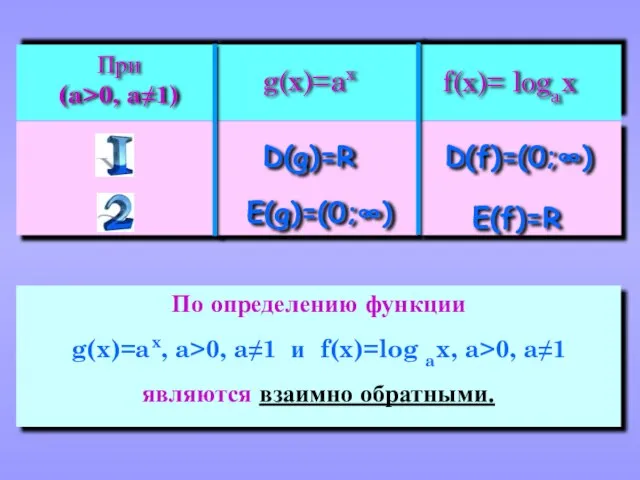
- 6. По определению функции g(x)=ax, a>0, a≠1 и f(x)=log ax, a>0, a≠1 являются взаимно обратными.
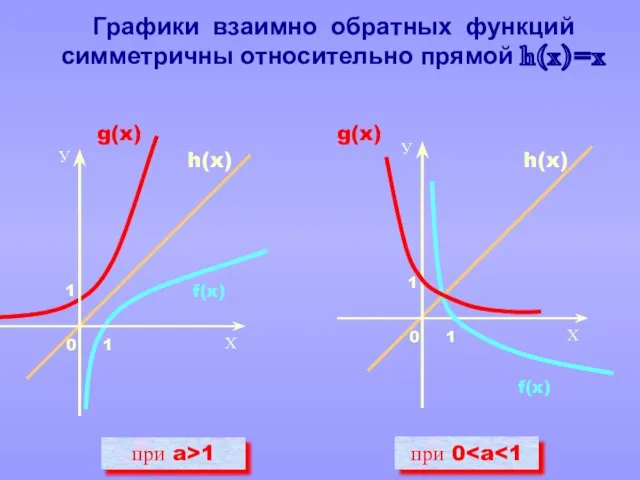
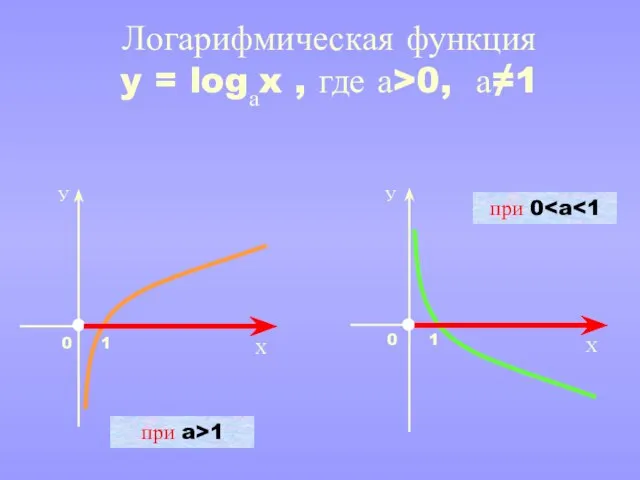
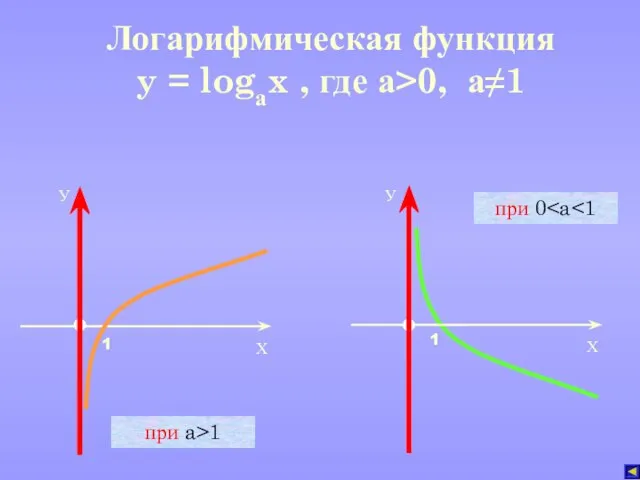
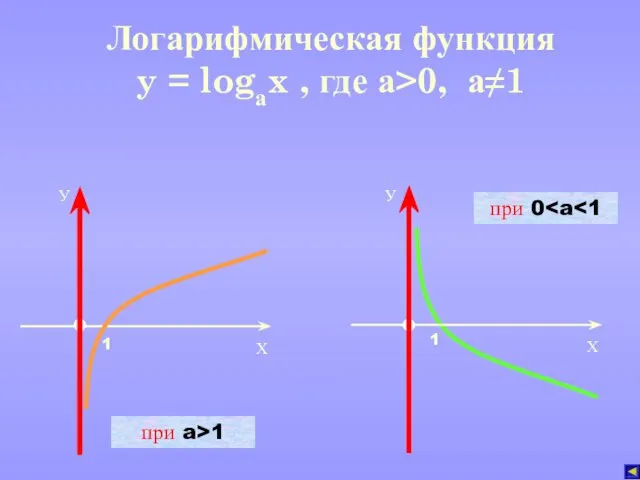
- 7. при a>1 при 0 g(x) g(x) h(x) h(x) f(x) f(x) Графики взаимно обратных функций симметричны относительно
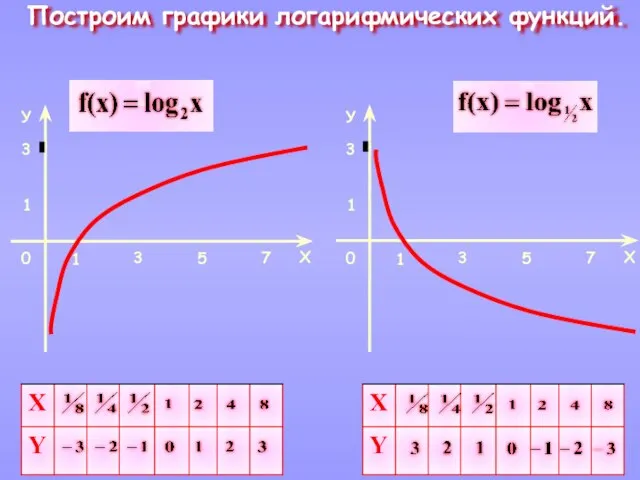
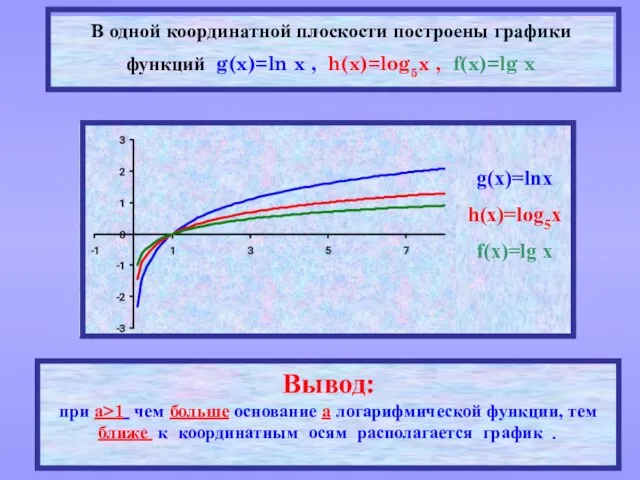
- 8. Построим графики логарифмических функций.
- 11. Какое значение аргумента х является допустимым для следующих функций:
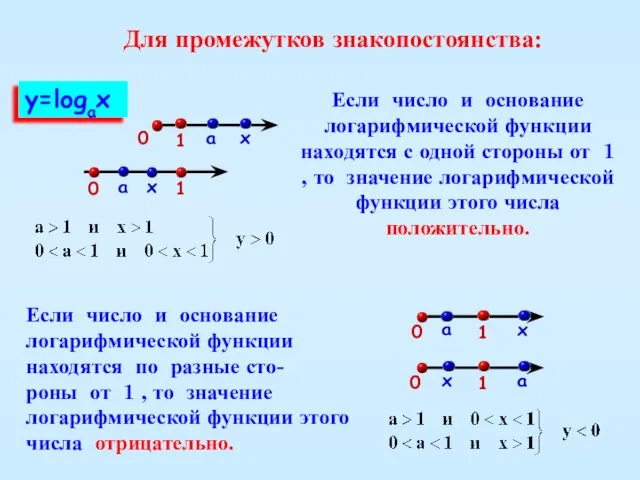
- 17. Для промежутков знакопостоянства: Если число и основание логарифмической функции находятся с одной стороны от 1 ,
- 18. Если число и основание логарифма лежат по одну сторону от 1, то логарифм положителен; Если число
- 19. Задание. Какое заключение можно сделать относительно числа m, если:
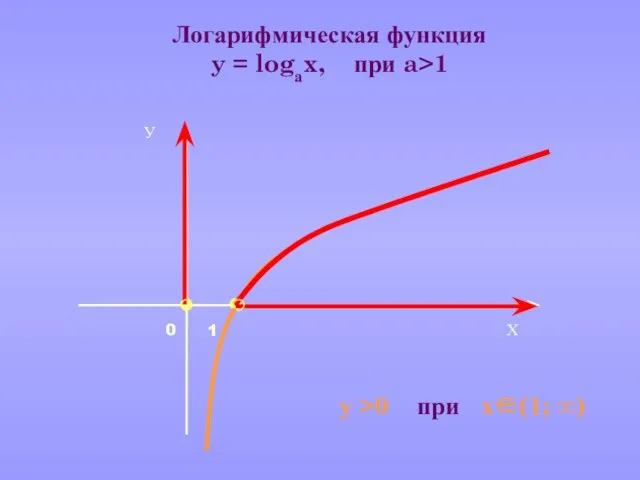
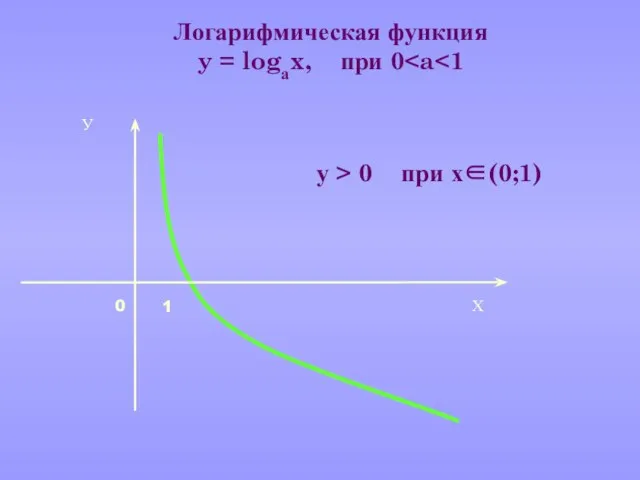
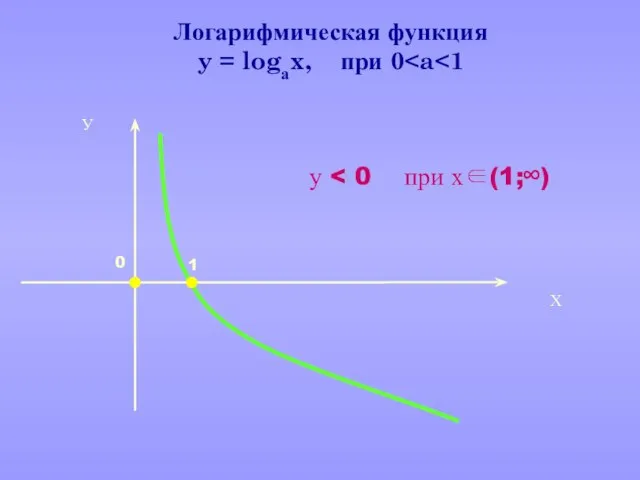
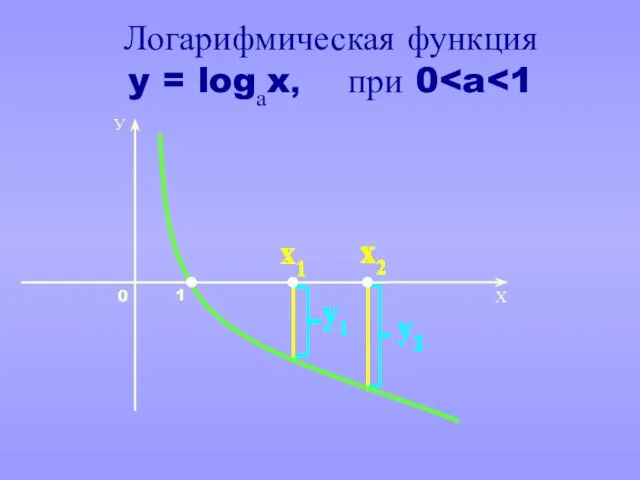
- 21. Логарифмическая функция y = logаx, при 0
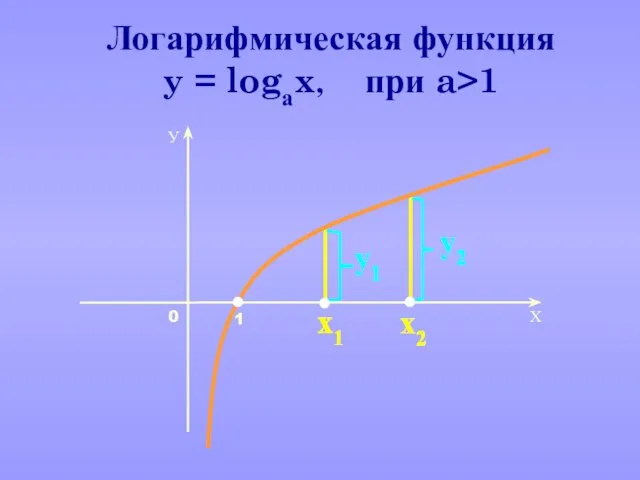
- 22. Какие из перечисленных ниже функций являются возрастающими, а какие убывающими? возрастающая, возрастающая, возрастающая, убывающая, убывающая,
- 23. Задание. Сравнить с 1 число а, если известно, что:
- 24. Задание. Между числами m и n поставить знак > или
- 28. Скачать презентацию










 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»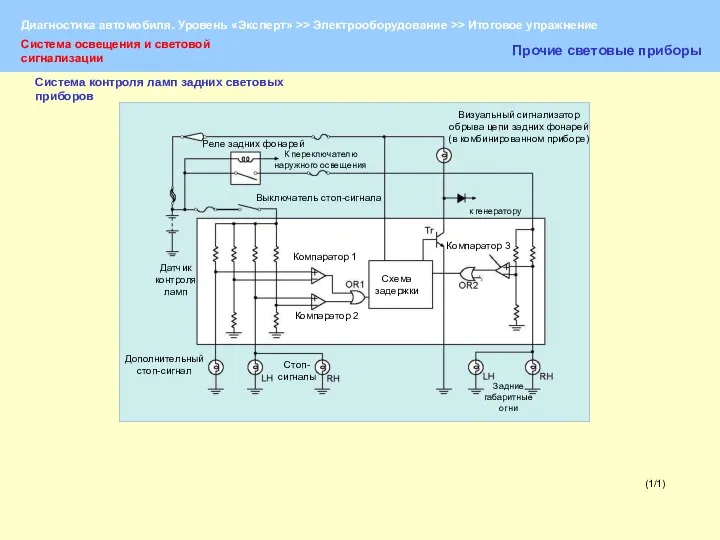 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс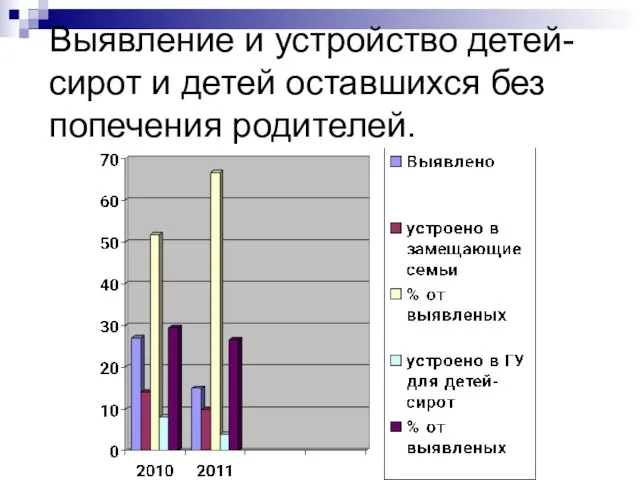 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства