Содержание
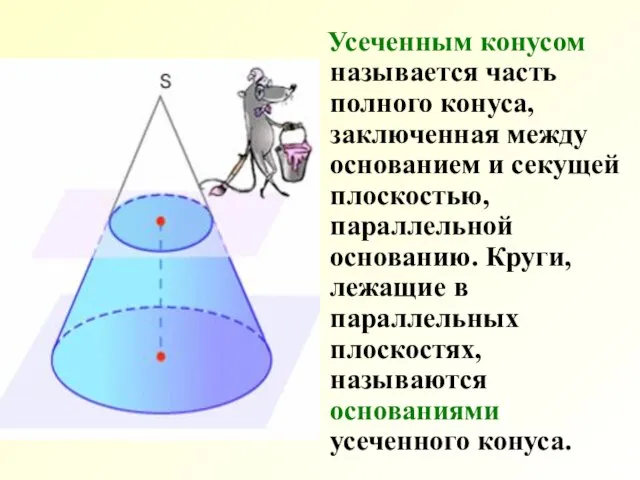
- 2. Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Круги, лежащие
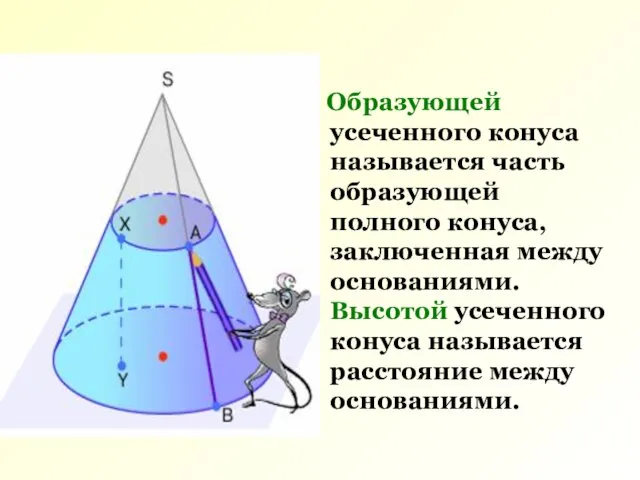
- 3. Образующей усеченного конуса называется часть образующей полного конуса, заключенная между основаниями. Высотой усеченного конуса называется расстояние
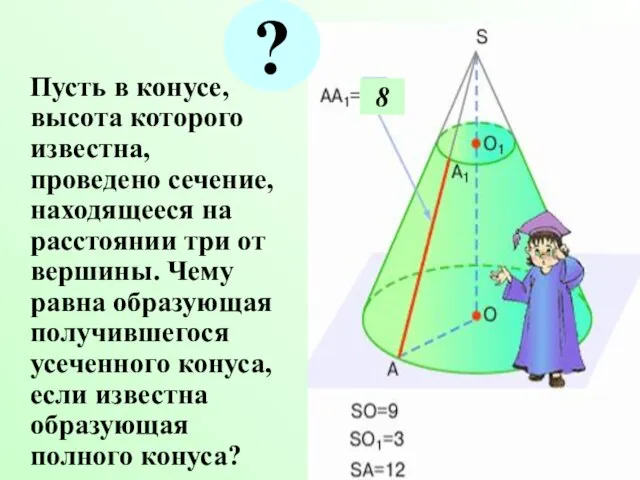
- 4. Пусть в конусе, высота которого известна, проведено сечение, находящееся на расстоянии три от вершины. Чему равна
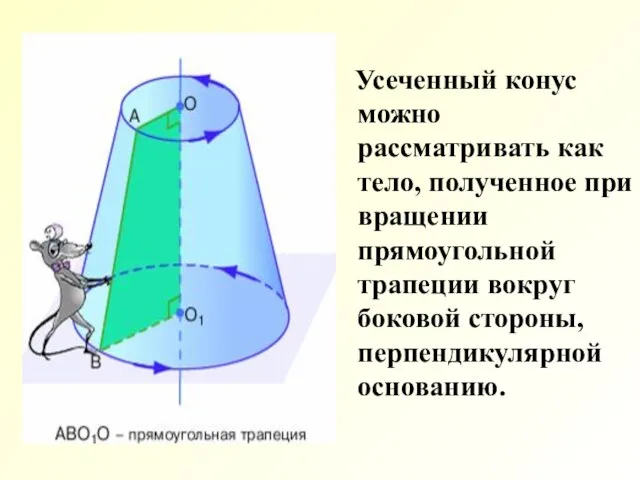
- 5. Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.
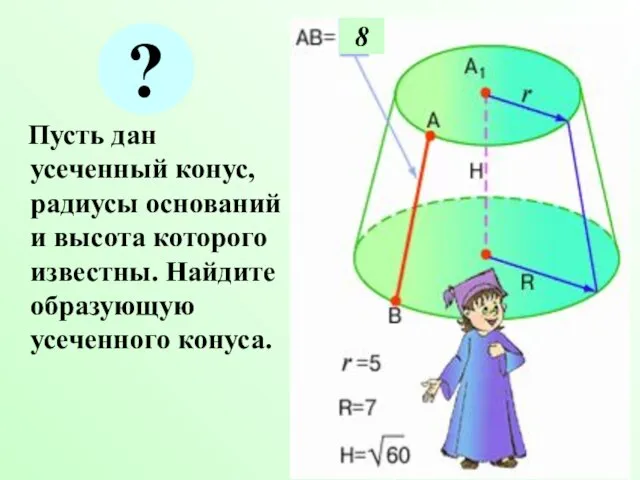
- 6. Пусть дан усеченный конус, радиусы оснований и высота которого известны. Найдите образующую усеченного конуса. 8 ?
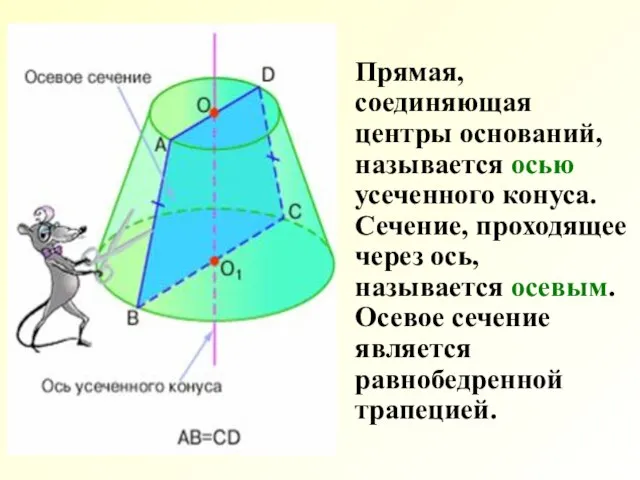
- 7. Прямая, соединяющая центры оснований, называется осью усеченного конуса. Сечение, проходящее через ось, называется осевым. Осевое сечение
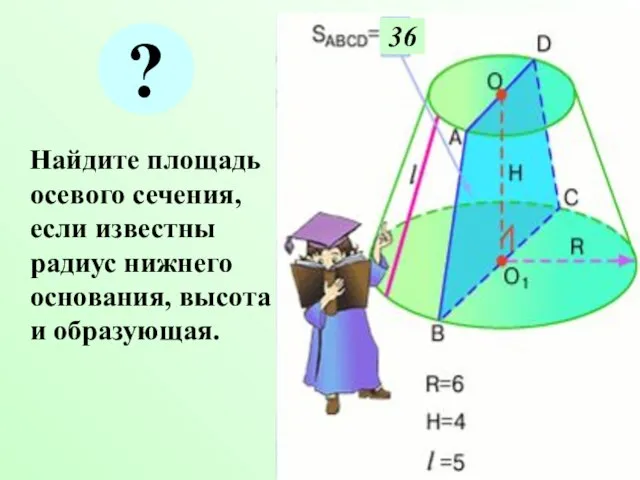
- 8. Найдите площадь осевого сечения, если известны радиус нижнего основания, высота и образующая. 36 ?
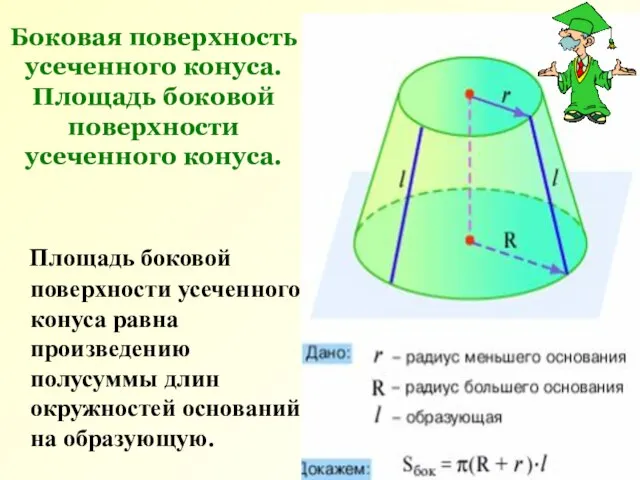
- 9. Боковая поверхность усеченного конуса. Площадь боковой поверхности усеченного конуса. Площадь боковой поверхности усеченного конуса равна произведению
- 10. Доказательство: Боковую поверхность усеченного конуса будем понимать как предел, к которому стремится боковая поверхность вписанной в
- 11. Доказательство: Впишем в конус правильную пирамиду. Ее боковая поверхность состоит из трапеций.
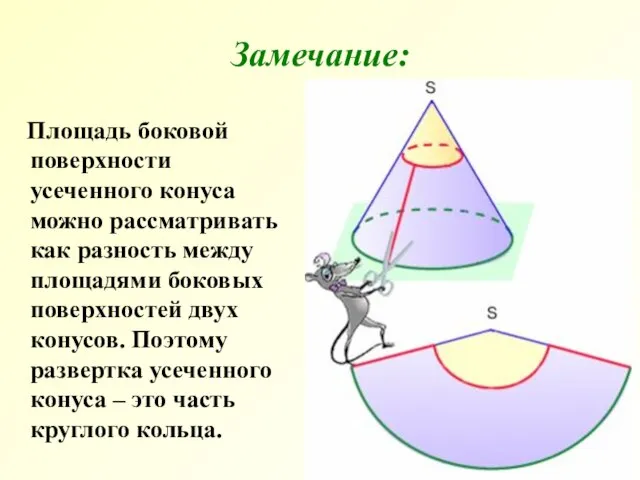
- 12. Площадь боковой поверхности усеченного конуса можно рассматривать как разность между площадями боковых поверхностей двух конусов. Поэтому
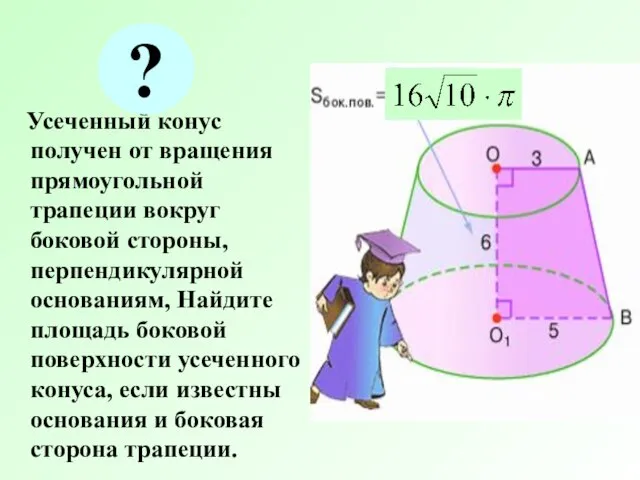
- 13. Усеченный конус получен от вращения прямоугольной трапеции вокруг боковой стороны, перпендикулярной основаниям, Найдите площадь боковой поверхности
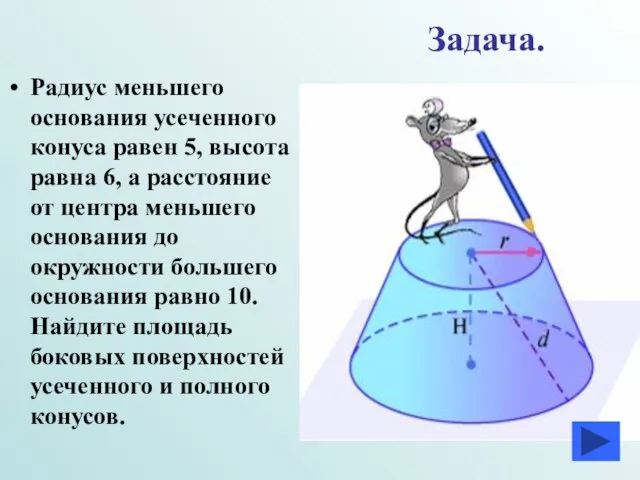
- 14. Задача. Радиус меньшего основания усеченного конуса равен 5, высота равна 6, а расстояние от центра меньшего
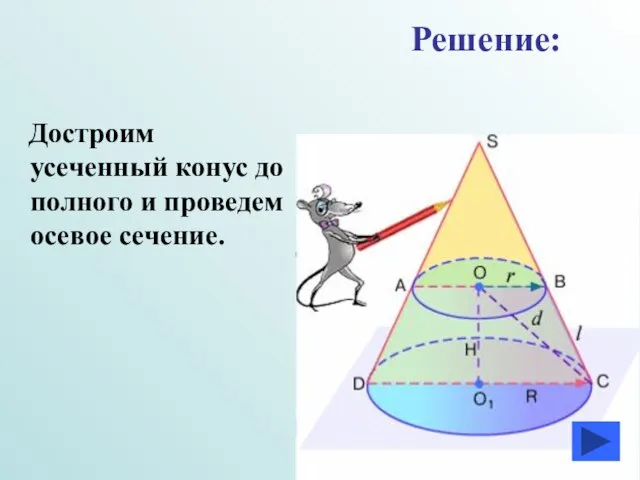
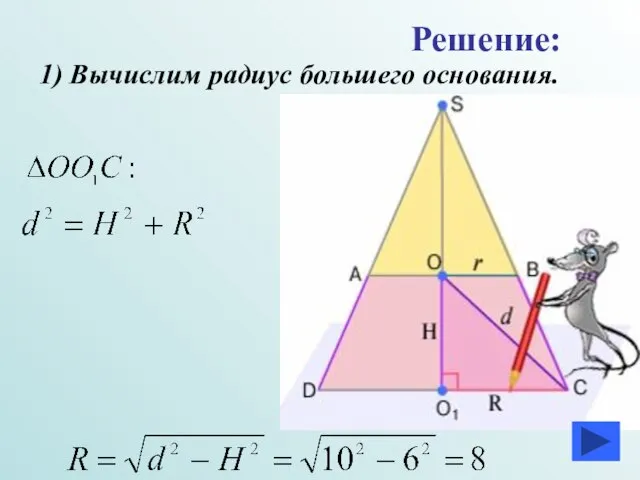
- 15. Достроим усеченный конус до полного и проведем осевое сечение. Решение:
- 16. 1) Вычислим радиус большего основания. Решение:
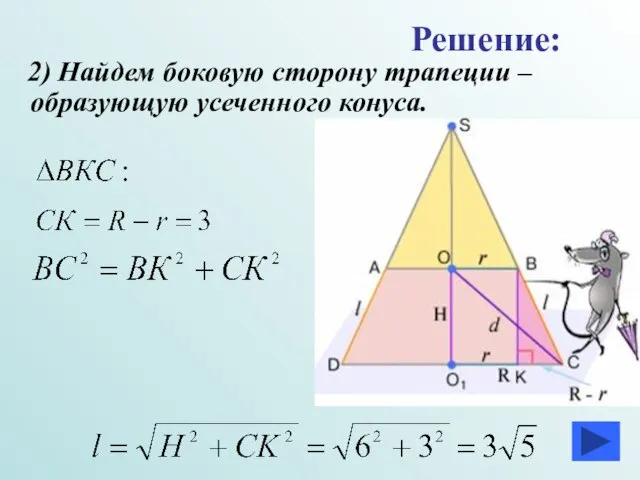
- 17. 2) Найдем боковую сторону трапеции –образующую усеченного конуса. Решение:
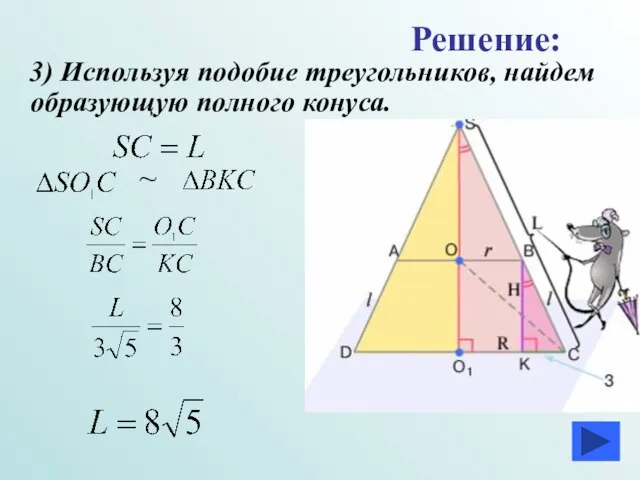
- 18. 3) Используя подобие треугольников, найдем образующую полного конуса. Решение: ~
- 19. 4) Подставим найденные значения в формулы для площадей боковой поверхности полного и усеченного конусов. Решение:
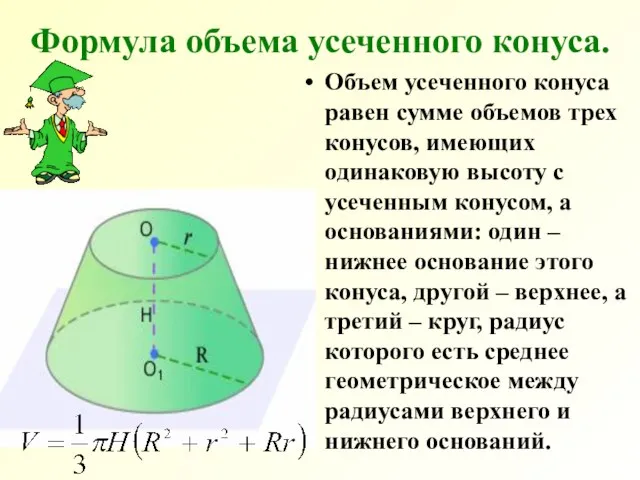
- 20. Формула объема усеченного конуса. Объем усеченного конуса равен сумме объемов трех конусов, имеющих одинаковую высоту с
- 21. Поместим на верхнем основании усеченного конуса малый конус, дополняющий его до полного и рассмотрим объем его
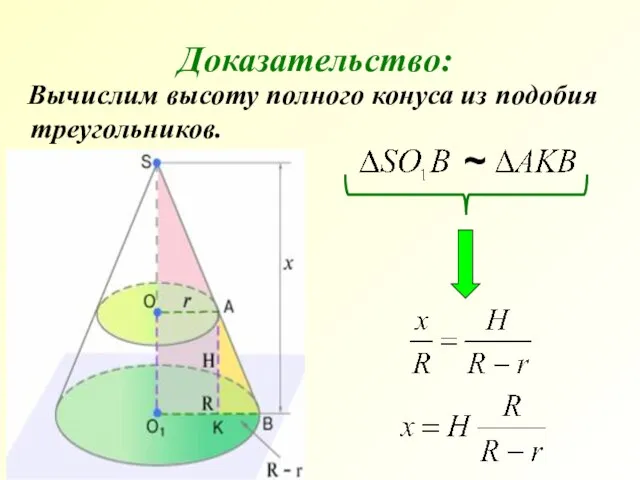
- 22. Вычислим высоту полного конуса из подобия треугольников. Доказательство: ~
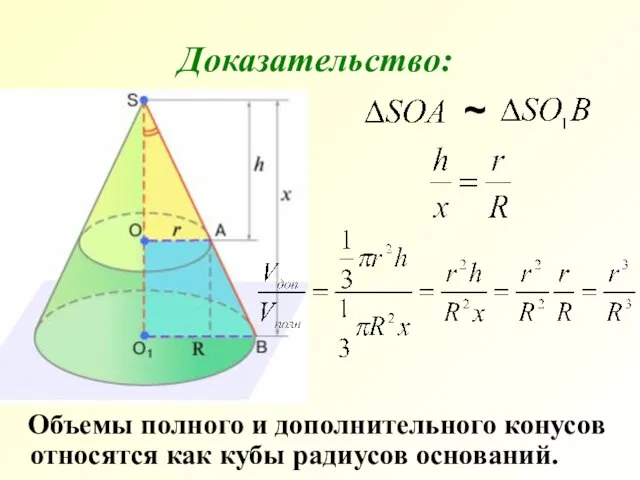
- 23. Объемы полного и дополнительного конусов относятся как кубы радиусов оснований. Доказательство: ~
- 24. Вычтем из объема большого конуса объем малого конуса. Доказательство:
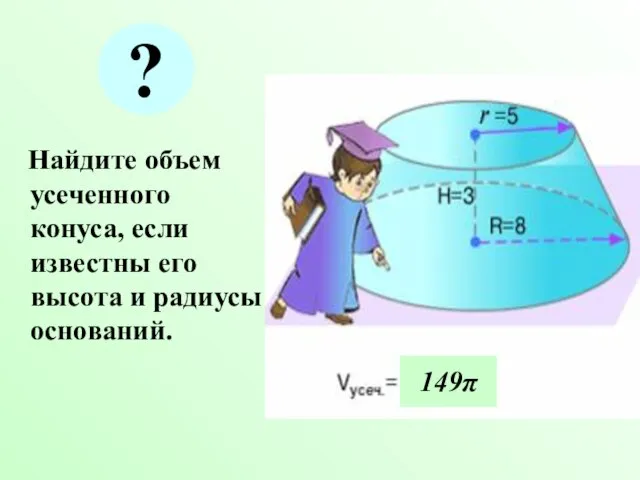
- 25. Найдите объем усеченного конуса, если известны его высота и радиусы оснований. 149π ?
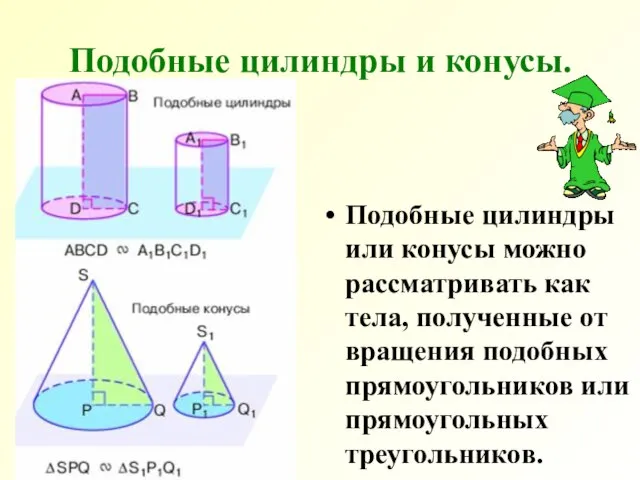
- 26. Подобные цилиндры и конусы. Подобные цилиндры или конусы можно рассматривать как тела, полученные от вращения подобных
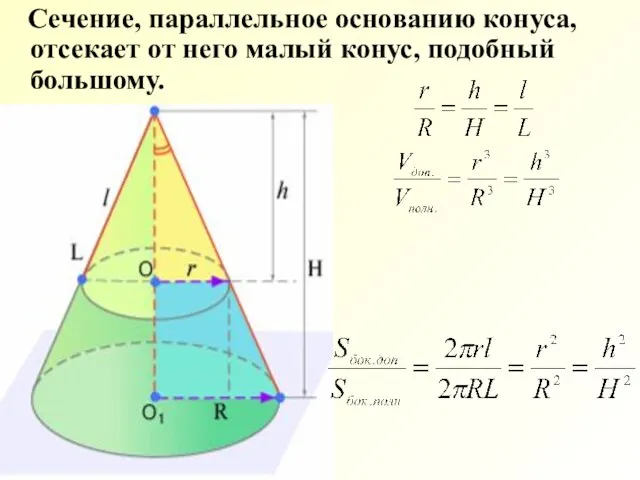
- 27. Сечение, параллельное основанию конуса, отсекает от него малый конус, подобный большому.
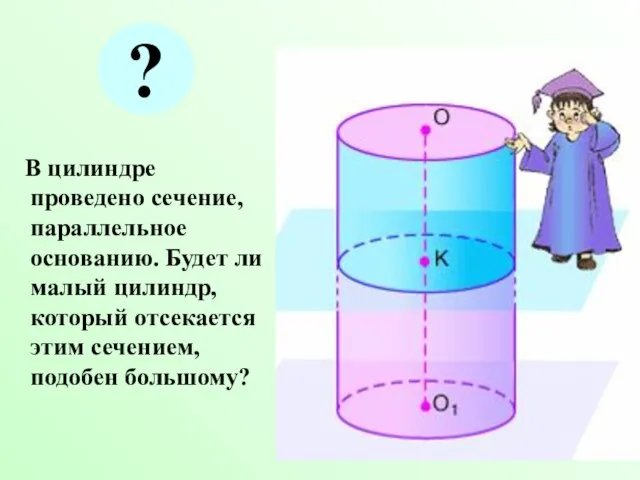
- 28. В цилиндре проведено сечение, параллельное основанию. Будет ли малый цилиндр, который отсекается этим сечением, подобен большому?
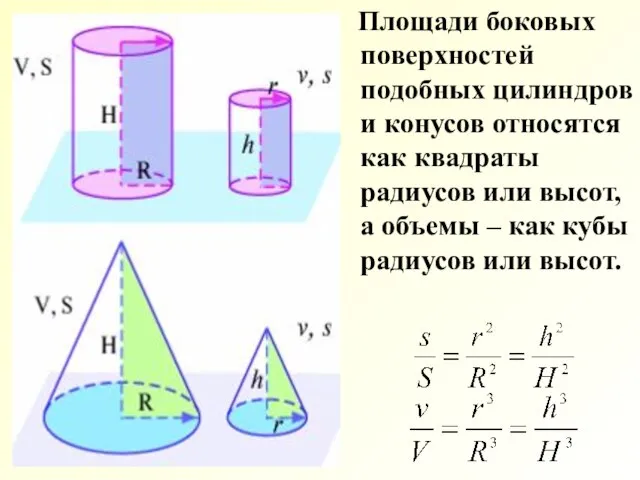
- 29. Площади боковых поверхностей подобных цилиндров и конусов относятся как квадраты радиусов или высот, а объемы –
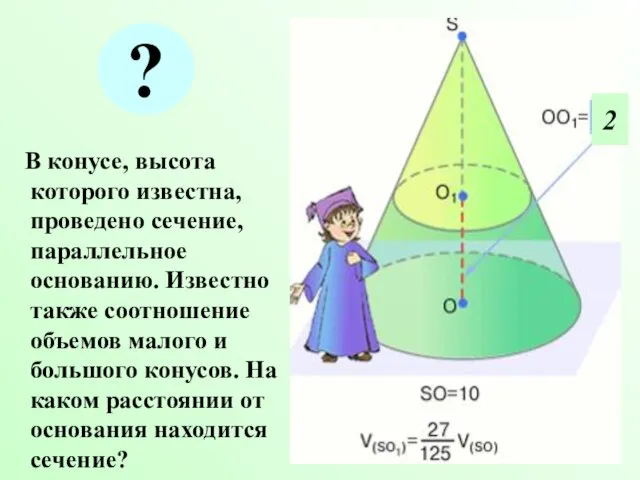
- 30. В конусе, высота которого известна, проведено сечение, параллельное основанию. Известно также соотношение объемов малого и большого
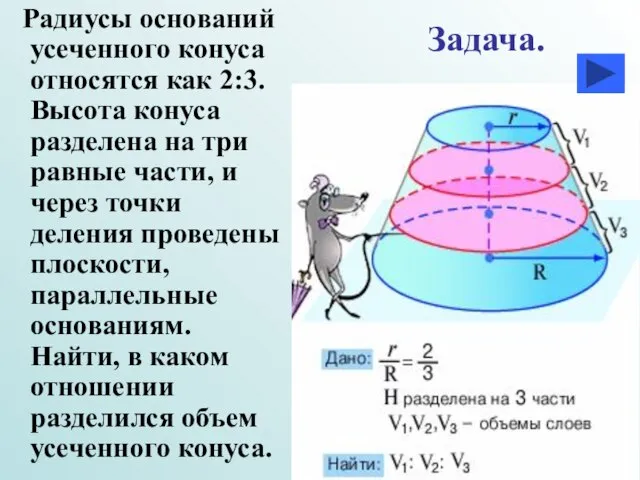
- 31. Радиусы оснований усеченного конуса относятся как 2:3. Высота конуса разделена на три равные части, и через
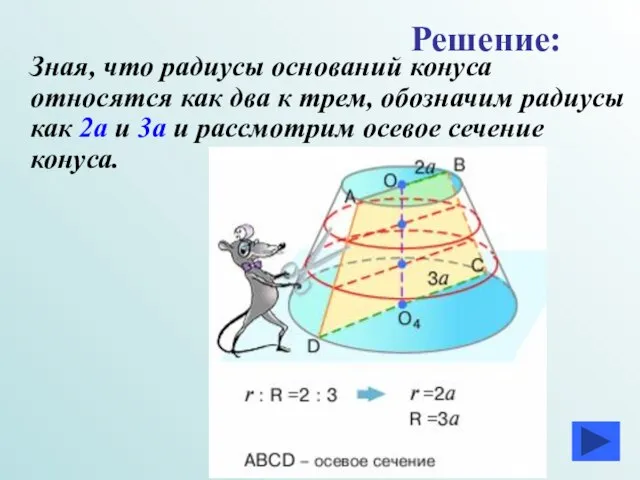
- 32. Зная, что радиусы оснований конуса относятся как два к трем, обозначим радиусы как 2а и 3а
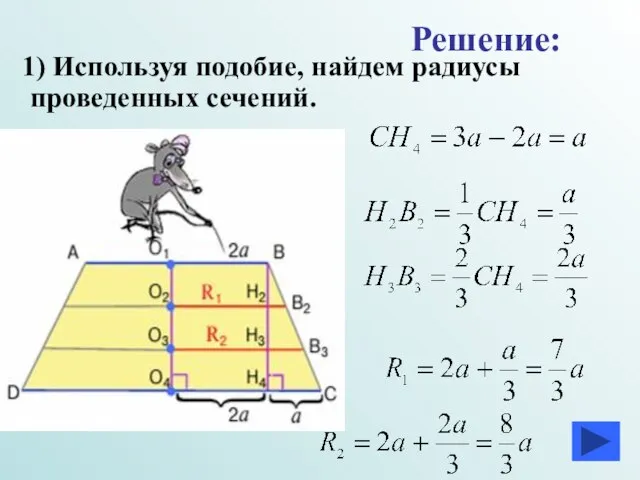
- 33. 1) Используя подобие, найдем радиусы проведенных сечений. Решение:
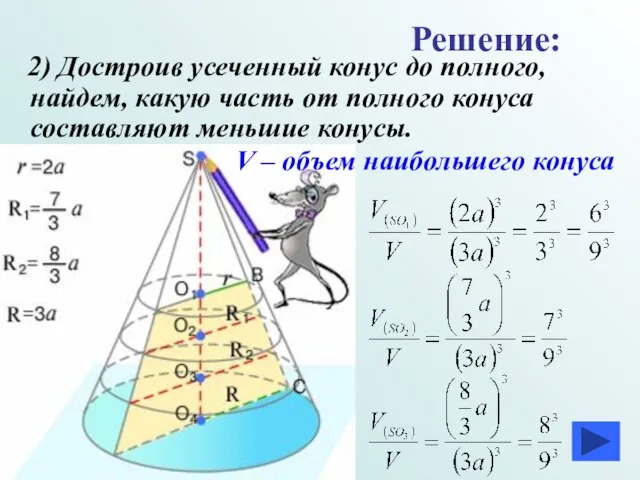
- 34. 2) Достроив усеченный конус до полного, найдем, какую часть от полного конуса составляют меньшие конусы. Решение:
- 36. Скачать презентацию





 Презентация на тему Вода - главный источник жизни
Презентация на тему Вода - главный источник жизни Презентация на тему Великие русские писатели
Презентация на тему Великие русские писатели  Использование игровых технологий на уроках географии
Использование игровых технологий на уроках географии Использование инновационных форм компьютерных технологий в обучении иностранному языку
Использование инновационных форм компьютерных технологий в обучении иностранному языку Основные понятия и определения изучаемые в разделе акробатика с элементами гимнастики
Основные понятия и определения изучаемые в разделе акробатика с элементами гимнастики Ostrov_mechty
Ostrov_mechty Физико - математические науки
Физико - математические науки Справится ли местоимение с ролью обращения?
Справится ли местоимение с ролью обращения? Современное и эффективное средство продвижения вашего продукта. Впервые на рынке Украины!
Современное и эффективное средство продвижения вашего продукта. Впервые на рынке Украины! Применение современных моделей автоматизации в профессиональной деятельности повара, кондитера
Применение современных моделей автоматизации в профессиональной деятельности повара, кондитера Крылатые крыловские слова
Крылатые крыловские слова Предупредим конфликт интересов. Викторина
Предупредим конфликт интересов. Викторина 70 лет снятия блокады Ленинграда
70 лет снятия блокады Ленинграда Культура Древнего Египта
Культура Древнего Египта  Свадебный рушник. Семейная реликвия семьи Коньшина Данила
Свадебный рушник. Семейная реликвия семьи Коньшина Данила TeleBingo new таблица
TeleBingo new таблица Программа фундаментальных исследований Президиума РАН № 27 «ОСНОВЫ ФУНДАМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ НАНОТЕХНОЛОГИЙ И НАНОМАТЕРИАЛО
Программа фундаментальных исследований Президиума РАН № 27 «ОСНОВЫ ФУНДАМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ НАНОТЕХНОЛОГИЙ И НАНОМАТЕРИАЛО Восточный базар
Восточный базар Презентация на тему Освоение Земли человеком (7 класс)
Презентация на тему Освоение Земли человеком (7 класс) Презентация на тему Второй и третий признаки подобия треугольников
Презентация на тему Второй и третий признаки подобия треугольников  Основы военной подготовки
Основы военной подготовки Презентация
Презентация Презентация на тему Технология обработки текстовой информации
Презентация на тему Технология обработки текстовой информации Манна
Манна 200-летию Победы России в Отечественной войне 1812 года посвящается
200-летию Победы России в Отечественной войне 1812 года посвящается Микрогибридные аккумуляторные технологии
Микрогибридные аккумуляторные технологии Социально-экономическое развитие пореформенной России в условиях экономического спада
Социально-экономическое развитие пореформенной России в условиях экономического спада Москва многонациональная
Москва многонациональная