Задачи на построение (7 класс)

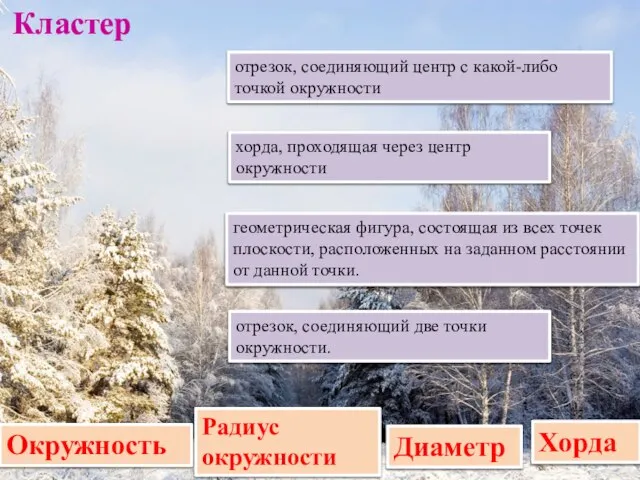
Окружность
геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Радиус окружности
отрезок, соединяющий центр с какой-либо точкой окружности
отрезок, соединяющий две точки окружности.
Хорда
хорда, проходящая через центр окружности
Диаметр
Кластер

Анализ. Нарисовать фигуру, установить связь между данными задачи и искомыми элементами, составить план решения задачи.
Построение. Выполняется по намеченному плану выполняется циркулем и линейкой.
Доказательство. Доказать, что построенная фигура удовлетворяет условиям задачи.
Исследование. Выяснить при любых ли данных задача имеет решение, и если имеет, то сколько решений.
Алгоритм решения задач на построение

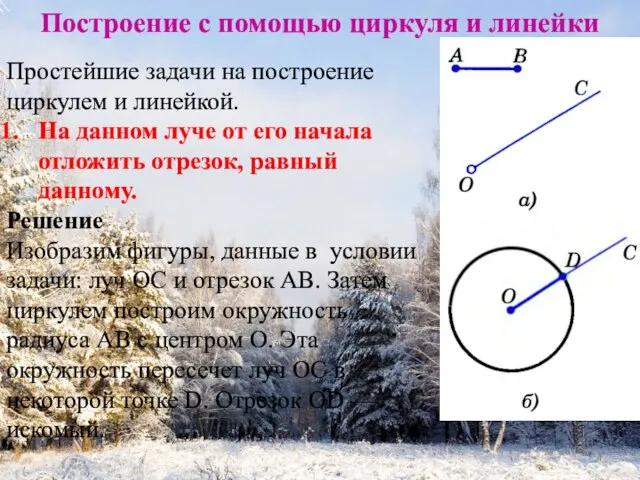
Построение с помощью циркуля и линейки
Простейшие задачи на построение циркулем и линейкой.
На данном луче от его начала отложить отрезок, равный данному.
Решение
Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ. Затем циркулем построим окружность радиуса АВ с центром О. Эта окружность пересечет луч ОС в некоторой точке D. Отрезок OD — искомый.

Построение с помощью циркуля и линейки
2. Отложить от данного луча угол, равный данному.
Решение
Данный угол с вершиной А и луч ОМ изображены на рисунке. Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ.
Проведем окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С (рис. а). Затем проведем окружность того же радиуса с центром в начале данного луча ОМ. Она пересекает луч в точке D (рис. б). После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е.

Построение с помощью циркуля и линейки
2. Отложить от данного луча угол, равный данному.
Докажем, что угол МОЕ — искомый. Рассмотрим треугольники ABC и ODE. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки OD и ОЕ — радиусами окружности с центром О (см. рис. б). Так как по построению эти окружности имеют равные радиусы, то AB = OD, АС = ОЕ. Также по построению ВС = DE. Следовательно, ABC = ODE по трем сторонам. Поэтому DOE = BAC, т. е. построенный угол МОЕ равен данному углу А.

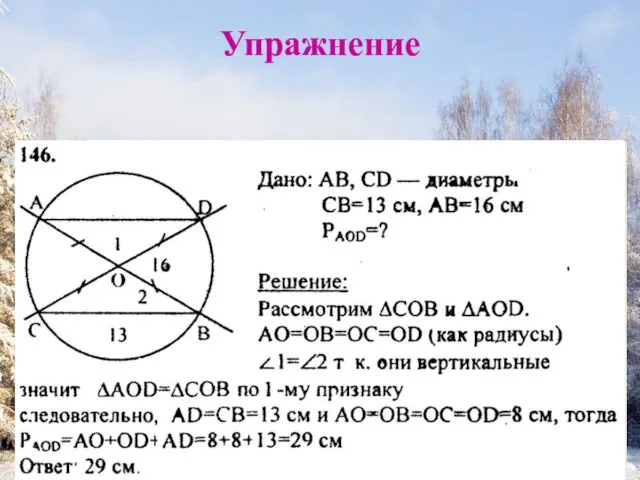
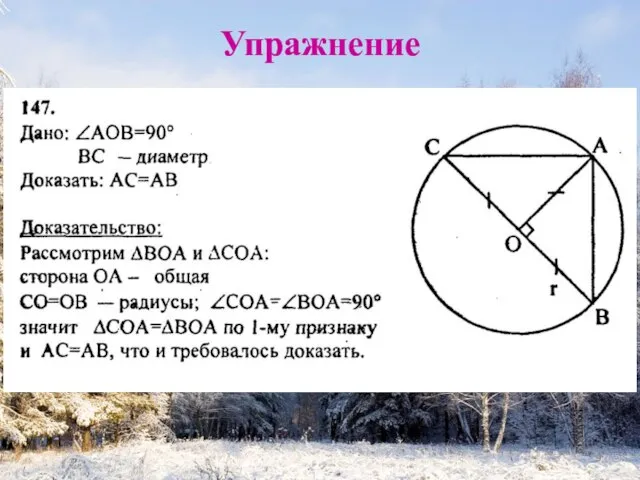
Упражнение
Решить задачи №№ 146, 147.

Упражнение

Упражнение

Задание на с/п:
Ответить на вопросы 17–21 на с. 50; решить задачи №№ 144, 145.

Синквейн
Окружность
Круглая, имеющая центр, радиус, диаметр, хорду,
Берем циркуль, чертим, отмечаем центр
все точки равноудаленные от данной точки плоскости
Похожа на обруч!