Содержание
- 2. Цель работы Получение точных аналитических решений задачи о нетепловых электронах в модели толстой мишени с обратным
- 3. Задачи Получить функцию распределения ускоренных электронов Рассчитать спектр и поляризацию жесткого рентгеновского излучения Оценить роль обратного
- 4. Для решения поставленных задач в работе применяется аналитический подход Численные расчеты в минимальном объеме применялись для
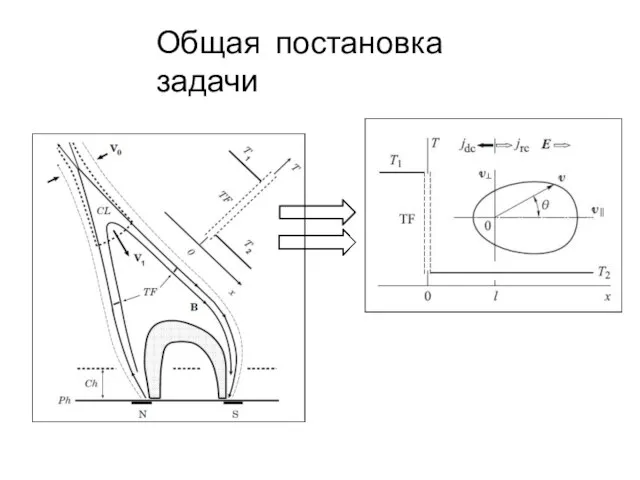
- 5. Общая постановка задачи
- 6. Главные предположения Внешнее магнитное поле однородное Процесс инжекции стационарный, распределение электронов в мишени установившееся Не рассматриваются
- 7. Поведение функции распределения электронов в мишени будем описывать кинетическим уравнением с интегралом столкновений Ландау: Введем безразмерные
- 8. В новых безразмерных переменных уравнение принимает вид:
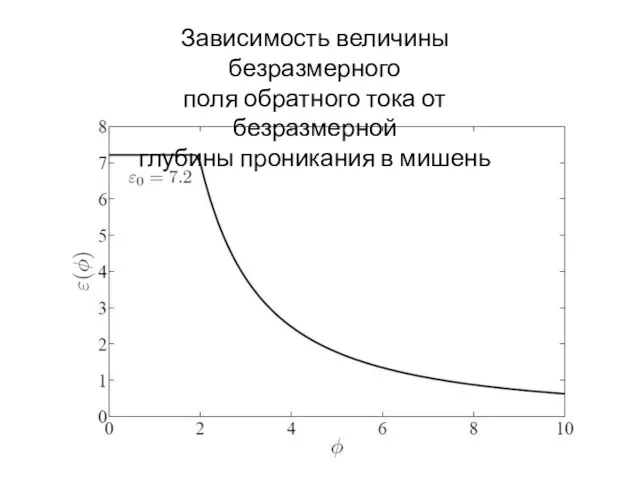
- 9. Зависимость величины безразмерного поля обратного тока от безразмерной глубины проникания в мишень
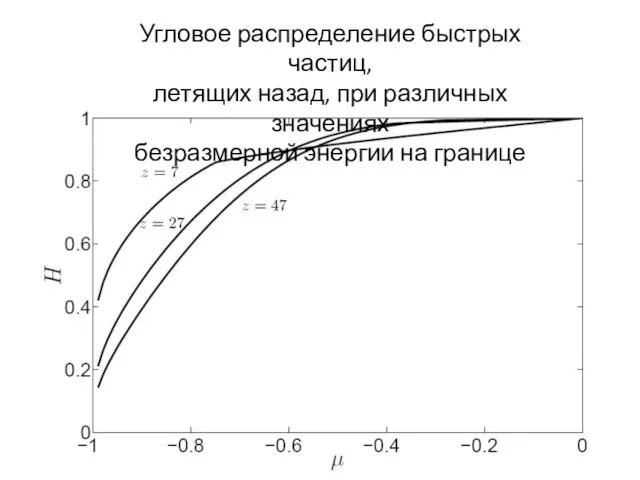
- 10. Угловое распределение быстрых частиц, летящих назад, при различных значениях безразмерной энергии на границе
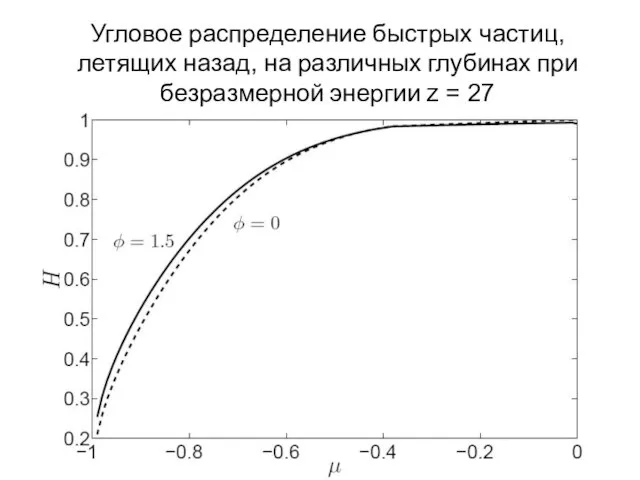
- 11. Угловое распределение быстрых частиц, летящих назад, на различных глубинах при безразмерной энергии z = 27
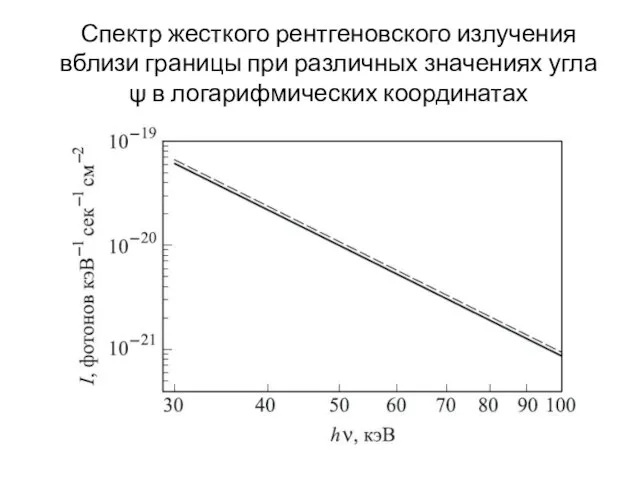
- 12. Спектр жесткого рентгеновского излучения вблизи границы при различных значениях угла ψ в логарифмических координатах
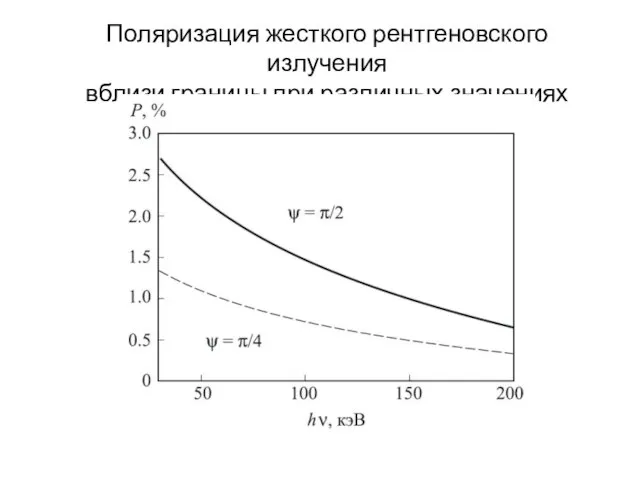
- 13. Поляризация жесткого рентгеновского излучения вблизи границы при различных значениях угла ψ
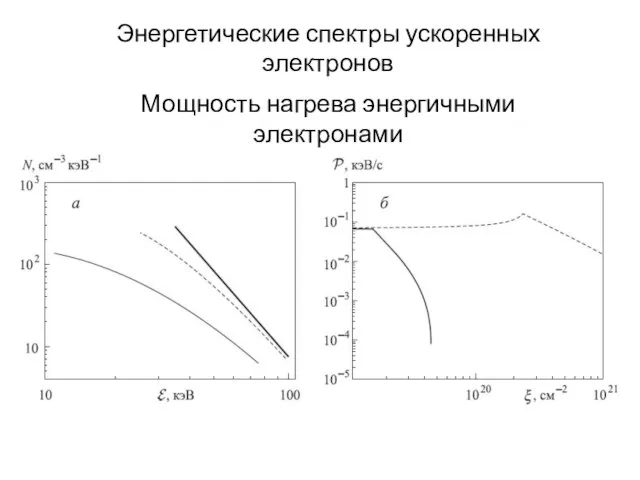
- 14. Энергетические спектры ускоренных электронов Мощность нагрева энергичными электронами плазмы в мишени
- 15. Выводы Потери энергии в электрическом поле обратного тока преобладают над потерями энергии на кулоновские столкновения Функция
- 17. Скачать презентацию







 7.1В_ Негативное влияние деятельности человека на экосистему_презентация
7.1В_ Негативное влияние деятельности человека на экосистему_презентация Древнейшие цивилизации
Древнейшие цивилизации Конструкция и декор предметов народного быта
Конструкция и декор предметов народного быта Почему так названы животные
Почему так названы животные «МОЯ РОДОСЛОВНАЯ»
«МОЯ РОДОСЛОВНАЯ» Порядок изменения цены контракта, корректировки
Порядок изменения цены контракта, корректировки Тема: Техногенные ЧС, возможные на территории Санкт – Петербурга. Потенциально опасные объекты, расположенные на территории субъ
Тема: Техногенные ЧС, возможные на территории Санкт – Петербурга. Потенциально опасные объекты, расположенные на территории субъ Участие прокурора в гражданском процессе по делам о защите прав и законных интересов неопределенного круга лиц
Участие прокурора в гражданском процессе по делам о защите прав и законных интересов неопределенного круга лиц The System Of State Bodies Of India
The System Of State Bodies Of India Урок 1. Где и когда ты живешь
Урок 1. Где и когда ты живешь Создание мультимедийной интерактивной презентации
Создание мультимедийной интерактивной презентации Закон на страже природы
Закон на страже природы Как открыть туристский клуб
Как открыть туристский клуб Презентация на тему Налоговые ставки: определение, виды
Презентация на тему Налоговые ставки: определение, виды  ПАМЯТНИКИ АНГЛИИ
ПАМЯТНИКИ АНГЛИИ Advanced SCP-RP
Advanced SCP-RP Флористика
Флористика Транспортные проблемы района Бирюлево-Западноеи меры по их улучшению.
Транспортные проблемы района Бирюлево-Западноеи меры по их улучшению. MarketLab’12 MarketLab’12 Интернет-маркетинг. Суть. Данность. Тренды. (куда мы движемся) киев 10 утра!
MarketLab’12 MarketLab’12 Интернет-маркетинг. Суть. Данность. Тренды. (куда мы движемся) киев 10 утра! Три клада у Природы есть:вода,Земля и воздух – три ее основы.Какая бы ни грянула беда,Целы они – все возродится снова.
Три клада у Природы есть:вода,Земля и воздух – три ее основы.Какая бы ни грянула беда,Целы они – все возродится снова.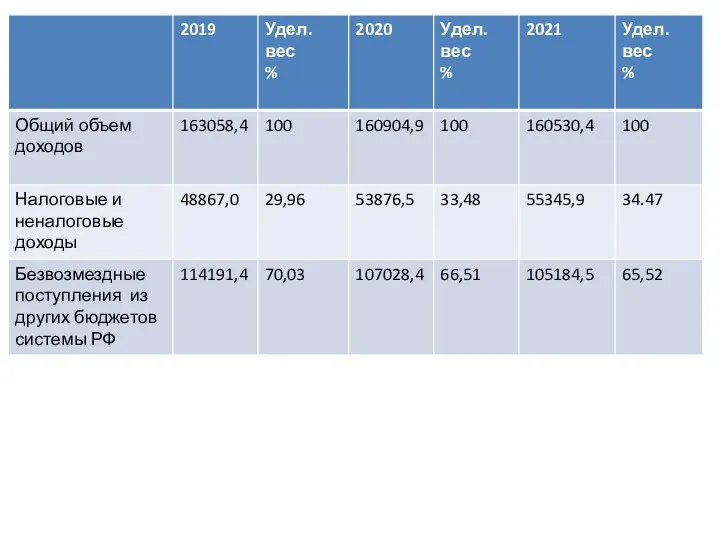 экономика батецкий
экономика батецкий ТВОРЧЕСКИЙ ОТЧЕТ
ТВОРЧЕСКИЙ ОТЧЕТ Презентация на тему Complex Object (Сложное дополнение)
Презентация на тему Complex Object (Сложное дополнение)  Рисунки Кучеровой Ксении, 13 лет
Рисунки Кучеровой Ксении, 13 лет Жидкостные предпусковые подогреватели «Теплостар»
Жидкостные предпусковые подогреватели «Теплостар» ЛОГИЧЕСКИЕ ОСНОВЫ ПК
ЛОГИЧЕСКИЕ ОСНОВЫ ПК Поступление в магистратуру
Поступление в магистратуру Занимательная информатика
Занимательная информатика