Содержание
- 2. Цель работы Целью данной курсовой работы является изучение устойчивости непрерывных решений систем дифференциальных уравнений первого порядка
- 3. Постановка задачи На основе изученного алгоритма проверить на устойчивость систему нелинейных дифференциальных уравнений подсчёта научной квалификации
- 4. Введение Анализ устойчивости непосредственно связан с определением условий равновесия. В линейных системах существуют только одно состояние
- 5. Целочисленный пример Рассматриваемая система дифференциальных уравнений является системой уравнений для оценки научной квалификации. uskor=3 I=125 U=12
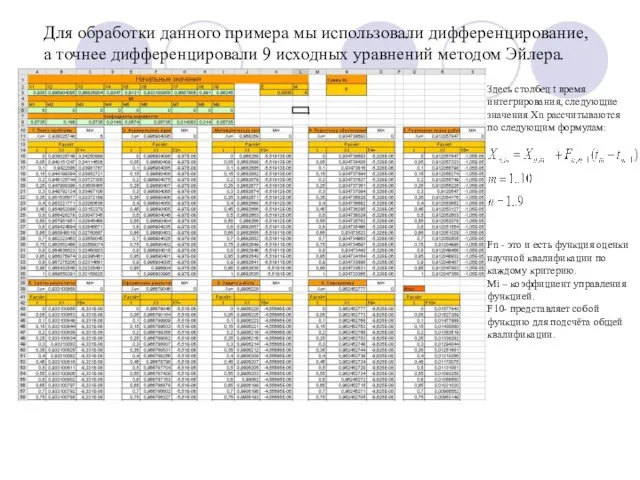
- 6. Для обработки данного примера мы использовали дифференцирование, а точнее дифференцировали 9 исходных уравнений методом Эйлера. Дифференцирование
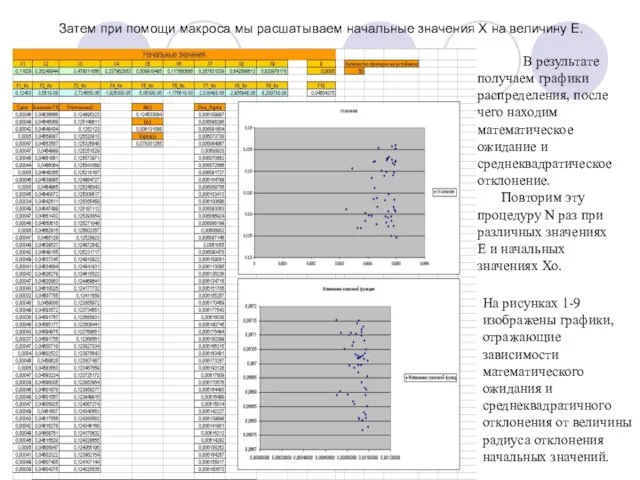
- 7. Затем при помощи макроса мы расшатываем начальные значения Х на величину Е. В результате получаем графики
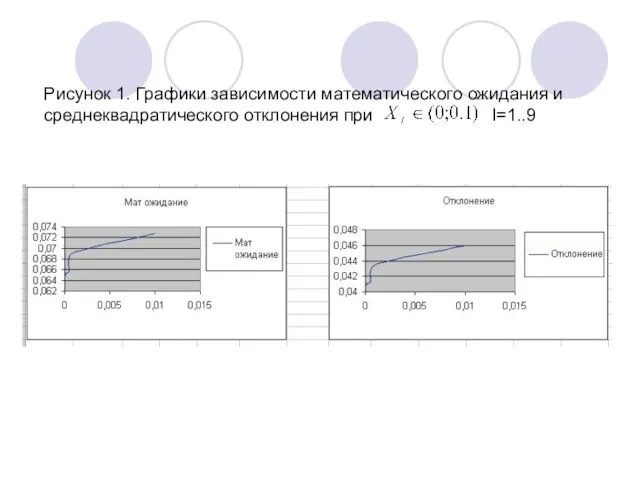
- 8. Рисунок 1. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
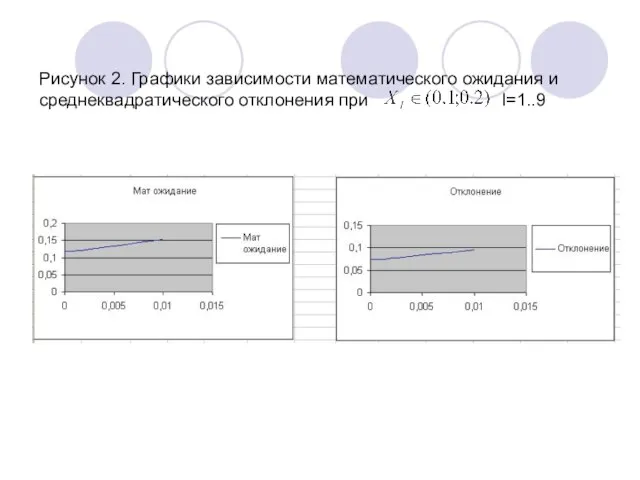
- 9. Рисунок 2. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
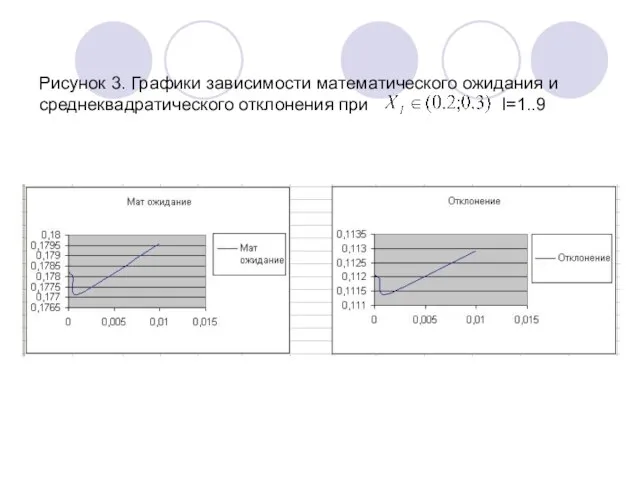
- 10. Рисунок 3. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
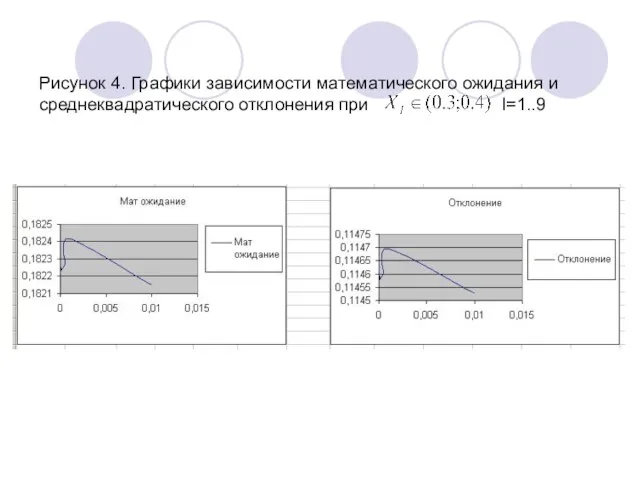
- 11. Рисунок 4. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
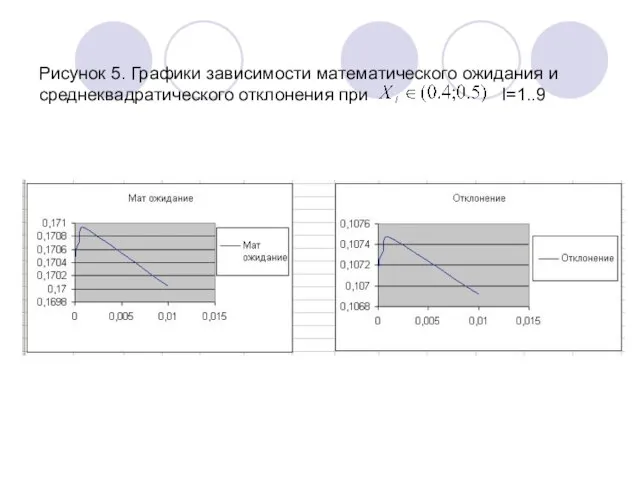
- 12. Рисунок 5. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
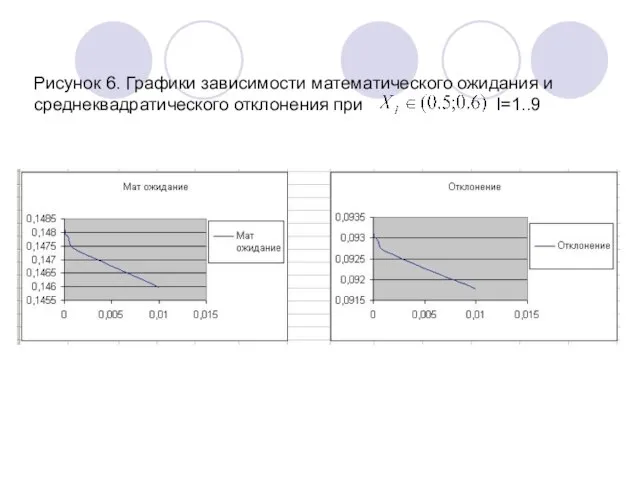
- 13. Рисунок 6. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
- 14. Рисунок 7. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
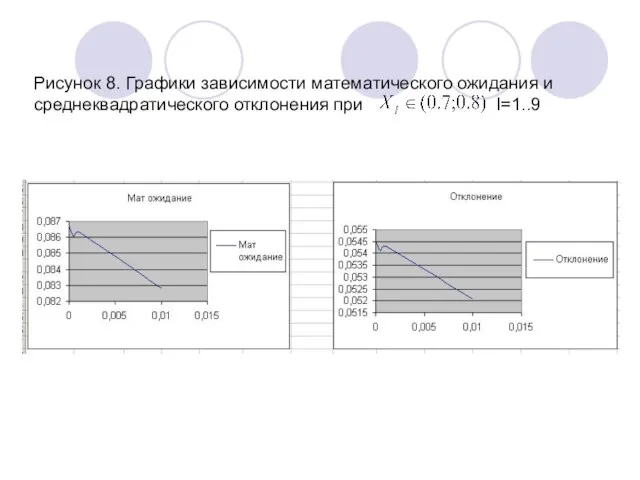
- 15. Рисунок 8. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
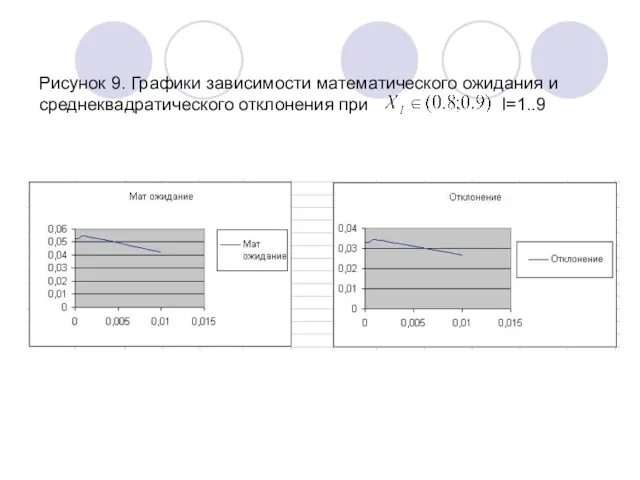
- 16. Рисунок 9. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
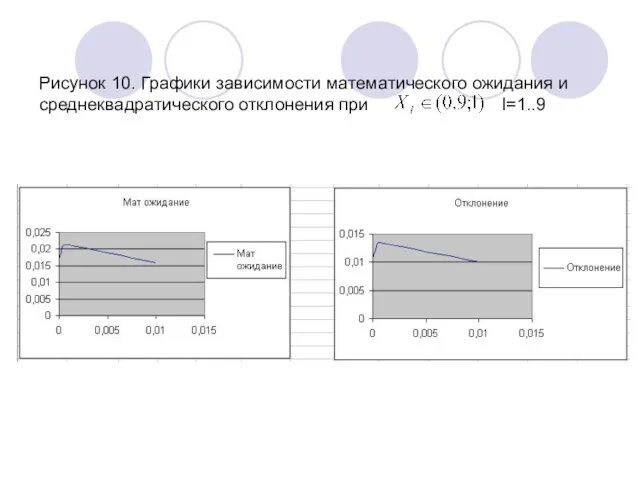
- 17. Рисунок 10. Графики зависимости математического ожидания и среднеквадратического отклонения при I=1..9
- 19. Скачать презентацию





 Опыт внедрения
Опыт внедрения Проблема поощрения и наказания младших школьников
Проблема поощрения и наказания младших школьников Приложение и документ.
Приложение и документ. 10 вопросов о Солнце
10 вопросов о Солнце Технология работы руководителя с неформальными лидерами и негативными микрогруппами в трудовом коллективе
Технология работы руководителя с неформальными лидерами и негативными микрогруппами в трудовом коллективе Викторина по ИЗО
Викторина по ИЗО Навстречу Олимпиаде
Навстречу Олимпиаде Prince Henry
Prince Henry У кого какая мама?
У кого какая мама? Меню. Шаурма, Узбекский плов
Меню. Шаурма, Узбекский плов Презентация на тему Коллективизация в Казахстане
Презентация на тему Коллективизация в Казахстане  НСОТ НПФ СОКО ГОУ СЕТИ
НСОТ НПФ СОКО ГОУ СЕТИ Азбука моих прав
Азбука моих прав Привычки хорошие и плохие
Привычки хорошие и плохие Кому в лесу жить хорошо
Кому в лесу жить хорошо Каримова Карина 11 класс
Каримова Карина 11 класс Урок №13. Превращение пешки
Урок №13. Превращение пешки Культурологический подход к преподаванию курса ОПК
Культурологический подход к преподаванию курса ОПК Презентация на тему Занятия горожан в старину
Презентация на тему Занятия горожан в старину Выбор профессии – первая жизненная проблема старшеклассника Над проектом работали: Ученики 9-а класса гимназии №3 Галя, Юля, Сере
Выбор профессии – первая жизненная проблема старшеклассника Над проектом работали: Ученики 9-а класса гимназии №3 Галя, Юля, Сере Показатели рыночной активности
Показатели рыночной активности Мастер – класс Осенние фантазии
Мастер – класс Осенние фантазии СОЗДАНИЕ СИСТЕМЫ ПЕРСОНАЛЬНОГО УЧЕТА НАСЕЛЕНИЯ В НИЖЕГОРОДСКОЙ ОБЛАСТИ
СОЗДАНИЕ СИСТЕМЫ ПЕРСОНАЛЬНОГО УЧЕТА НАСЕЛЕНИЯ В НИЖЕГОРОДСКОЙ ОБЛАСТИ Велесов день - середина зимы. Фольклорное путешествие
Велесов день - середина зимы. Фольклорное путешествие Русская архитектура XIX века
Русская архитектура XIX века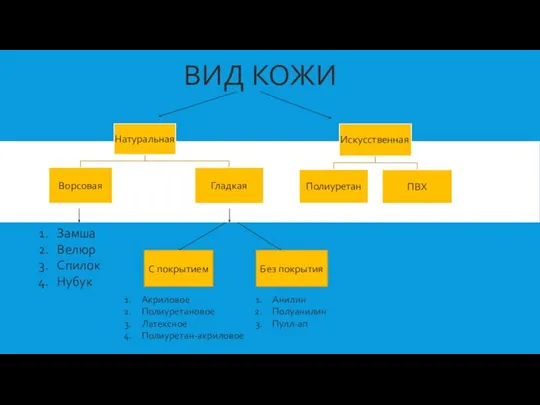 Виды кож
Виды кож Здоровье школьников
Здоровье школьников STM-1/4 STM-4/16
STM-1/4 STM-4/16