В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число

Радиоактивный распад ― масса вещества за равные промежутки времени изменяется в одном и том же соотношении.
Вы все слышали о цепных реакциях, теорию которых в 20-ых годах описал
молодой химик Н.Н.Семенов, а потом развили ученые-атомщики. Как управлять
этим процессом в мирных целях? На этот вопрос можно ответить только при
помощи знаний о показательной функции.

Колония бактерий, при благоприятных условиях, изменяет свою массу за равные промежутки времени в одном и том же соотношении.
Рост бактерий в идеальных условиях
соответствует процессу органического роста.

Нобелевские лауреаты
Тема «Показательная функция» является основополагающей при изучении таких тем как, «Производная показательной функции», «Термодинамика», «Электромагнетизм», «Ядерная физика», « Колебания», используется для решения некоторых задач судовождения. Вот некоторые из Нобелевских лауреатов, получивших премию за исследования в области физики с использованием показательной функции
Пьер Кюри - 1903г.
Ричардсон Оуэн - 1928г.
Игорь Тамм - 1958
Альфарес Луис - 1968г.
Альфвен Ханнес - 1970г.
Вильсон Роберт Вудро - 1978г.

Показательная функция

Закончите равенства:
Степень с рациональным показателем

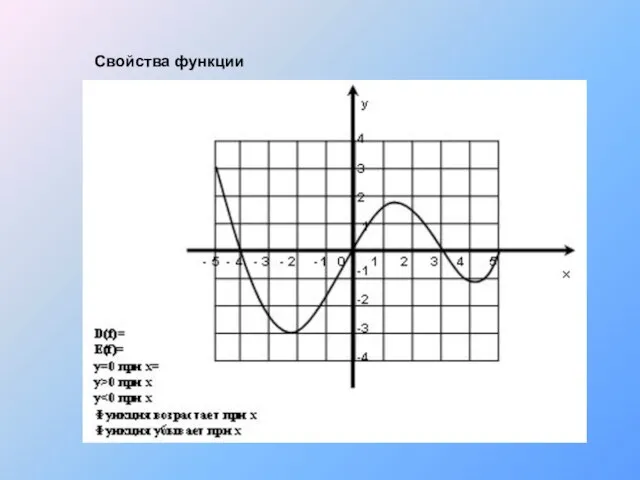
Свойства функции

Запишите выражение в виде степени числа 3 с рациональным показателем.

Запишите выражение в виде степени числа 3 с рациональным показателем.
у = 3t

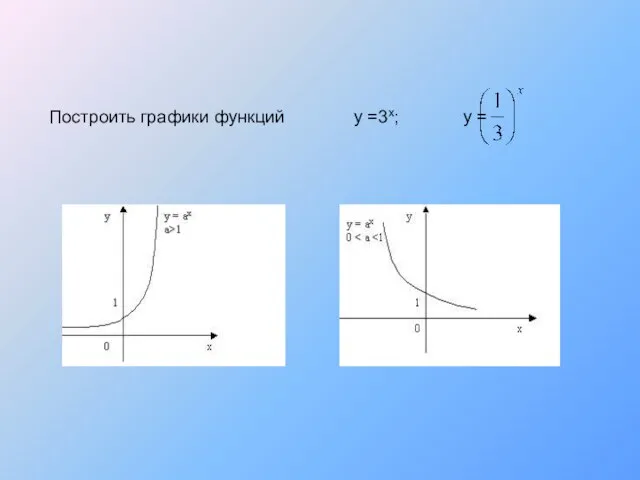
Построить графики функций у =3х; у =

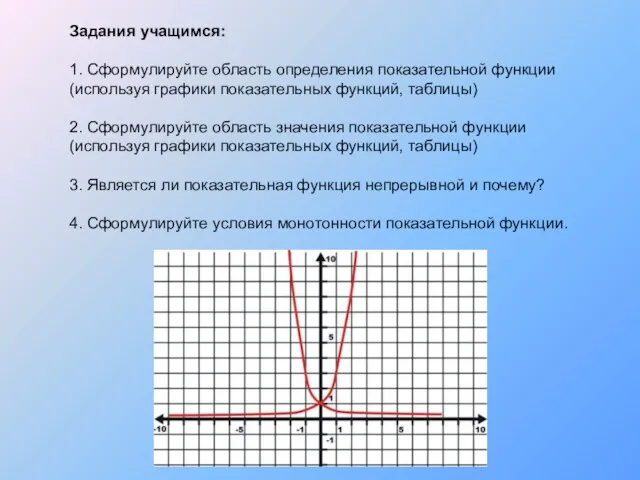
Задания учащимся:
1. Сформулируйте область определения показательной функции(используя графики показательных функций, таблицы)
2. Сформулируйте область значения показательной функции(используя графики показательных функций, таблицы)
3. Является ли показательная функция непрерывной и почему?
4. Сформулируйте условия монотонности показательной функции.

Свойства показательной функции
1. D(f) = R, так как x – любое число
2. E(f) = R+
3. Функция непрерывна
4. Функция возрастает при a >1, функция убывает при 0 < a < 1
5. При любых действительных значениях x и y справедливы равенства

1. Перечислите свойства функции и схематично постройте её график:
2. Найдите координаты точек пересечения графиков функций:
у = и у = 9

Самостоятельная работа