Содержание
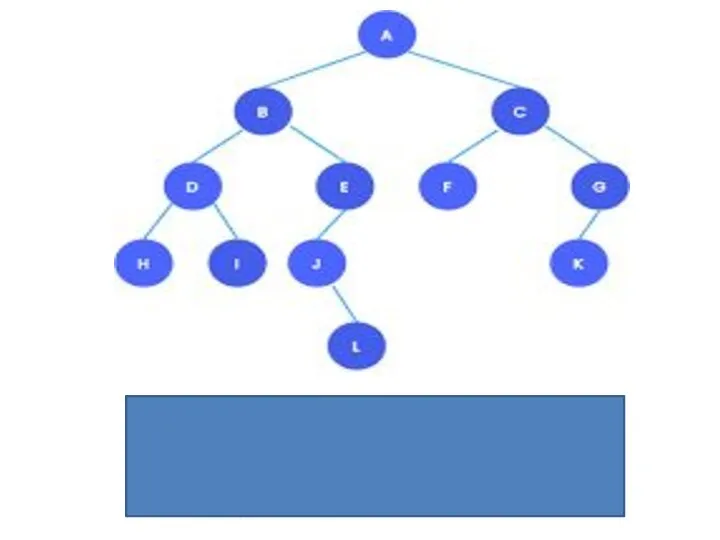
- 2. Traversing a Binary Tree Traversing a binary tree is the process of visiting each node in
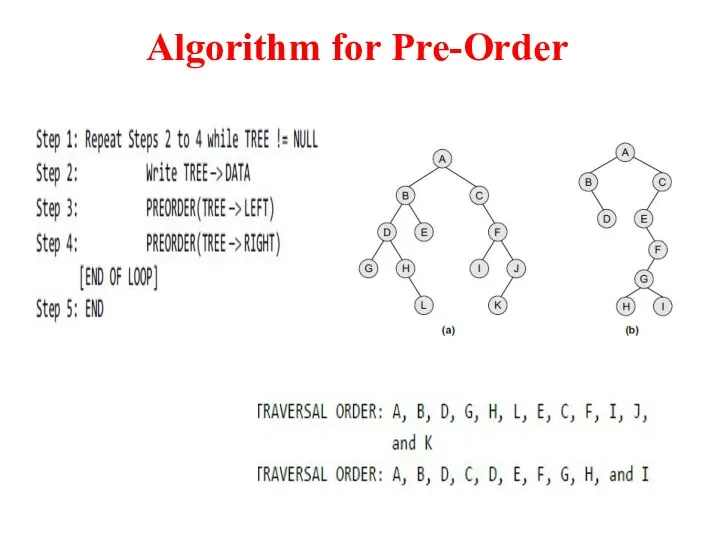
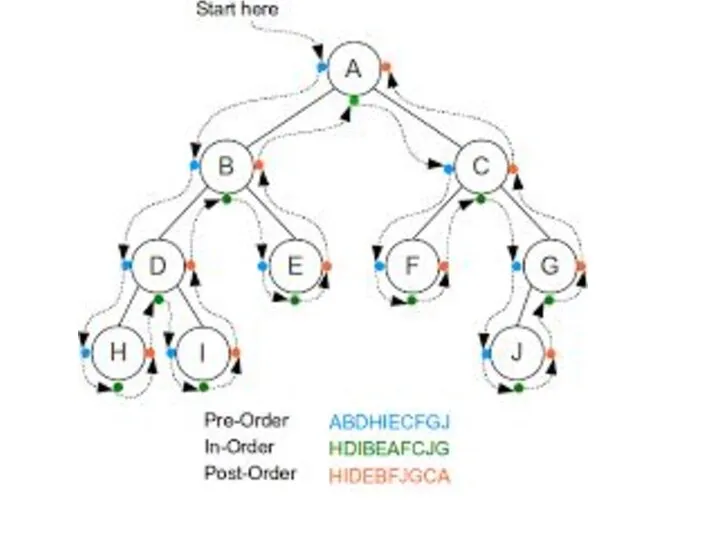
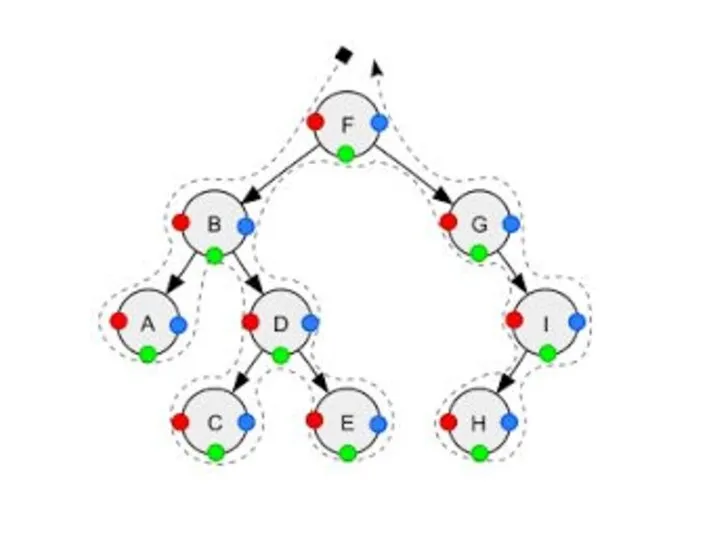
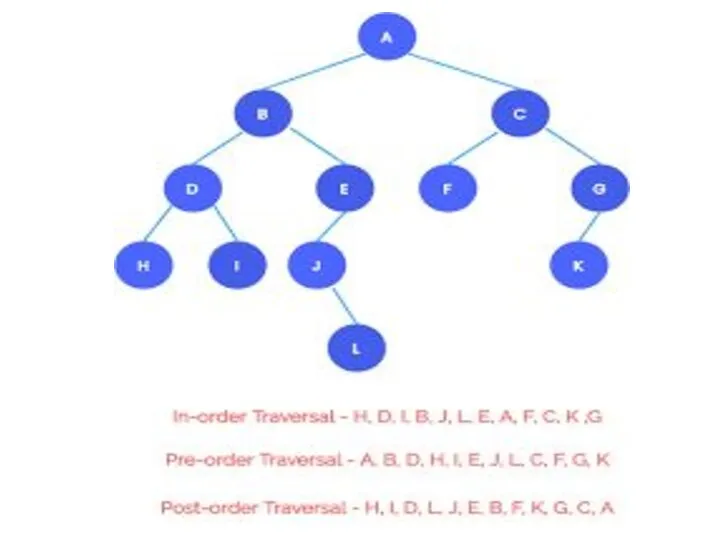
- 3. Pre-order Traversal To traverse a non-empty binary tree in pre-order, the following operations are performed recursively
- 4. Algorithm for Pre-Order
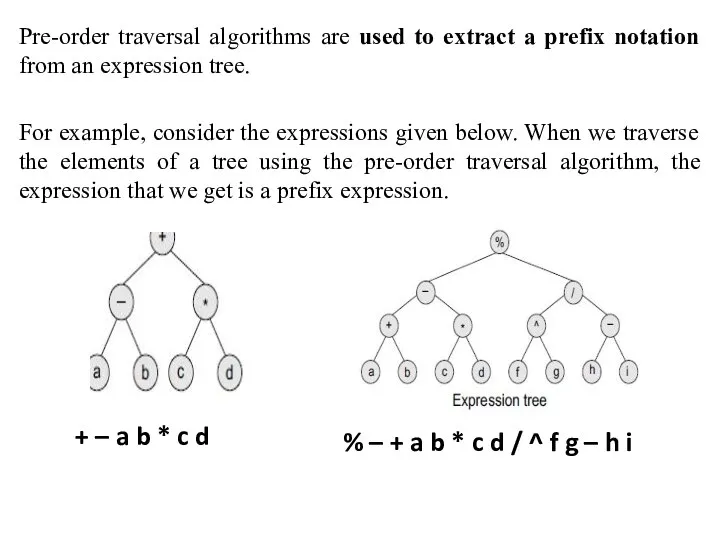
- 5. Pre-order traversal algorithms are used to extract a prefix notation from an expression tree. For example,
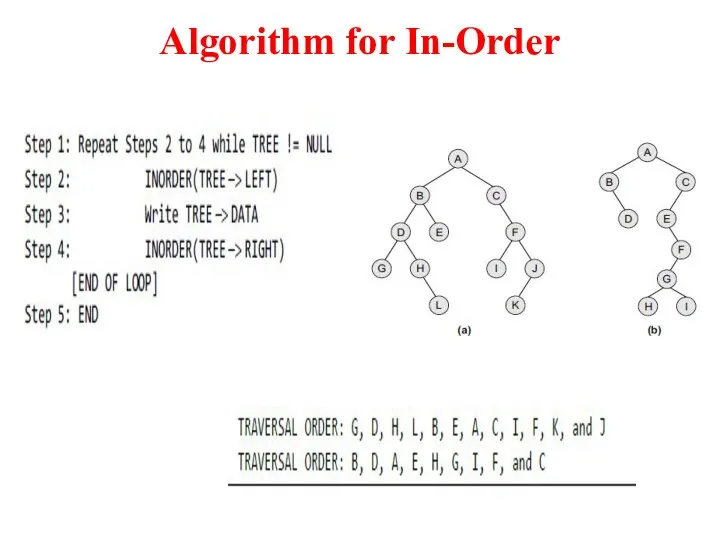
- 6. In-order Traversal To traverse a non-empty binary tree in in-order, the following operations are performed recursively
- 7. Algorithm for In-Order
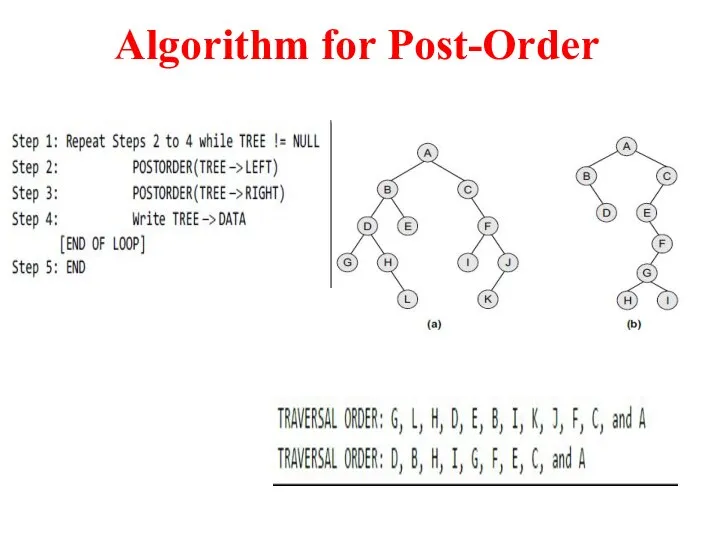
- 8. Post-Order Traversal To traverse a non-empty binary tree in post-order, the following operations are performed recursively
- 9. Algorithm for Post-Order
- 14. Binary Search Tree
- 15. Binary Search Tree A binary search tree, also known as an ordered binary tree, is a
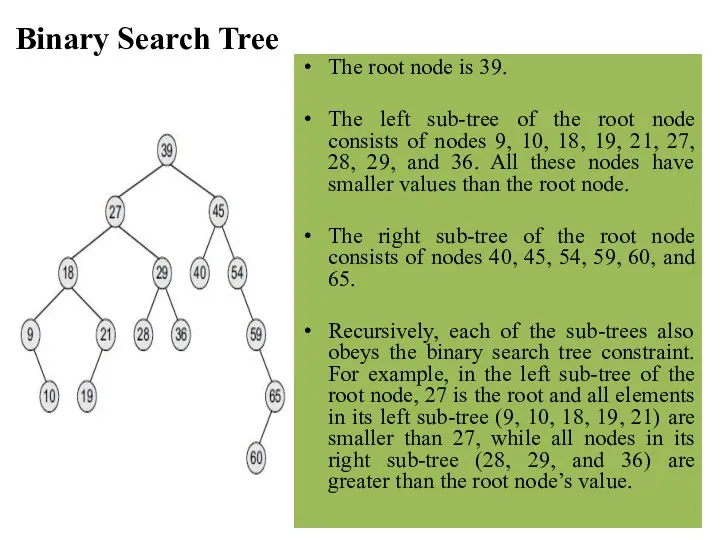
- 16. Binary Search Tree The root node is 39. The left sub-tree of the root node consists
- 17. Binary Search Tree - Operations Binary search trees speed up the insertion and deletion operations. The
- 18. To summarize, a binary search tree is a binary tree with the following properties: The left
- 19. Binary Search tree Operations
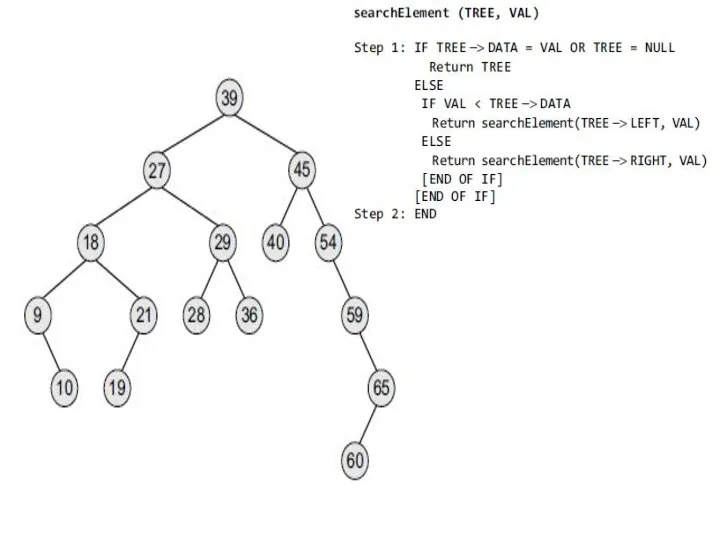
- 20. Searching for a node in Binary Search Tree
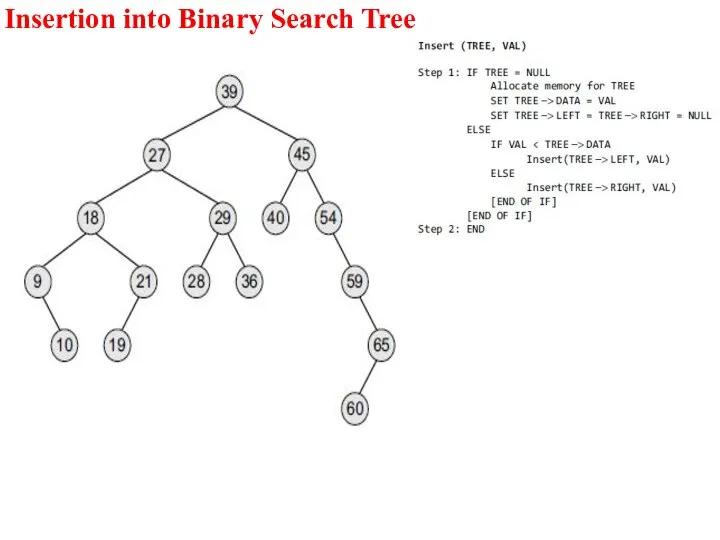
- 22. Insertion into Binary Search Tree
- 23. Insertion into Binary Search Tree
- 24. Construct Binary Search Tree by inserting following Nodes 39,27,45,18,29,40,9,21,10,19,54,59,65,60
- 25. Node Deletion Binary Search Tree
- 26. Deletion from Binary Search Tree Case 1: Deleting a Node that has No Children binary search
- 27. Case 2: Deleting a Node with One Child the node’s child is set as the child
- 28. Case 3: Deleting a Node with Two Children Replace the node’s value with its in-order predecessor
- 29. Algorithm for Deletion
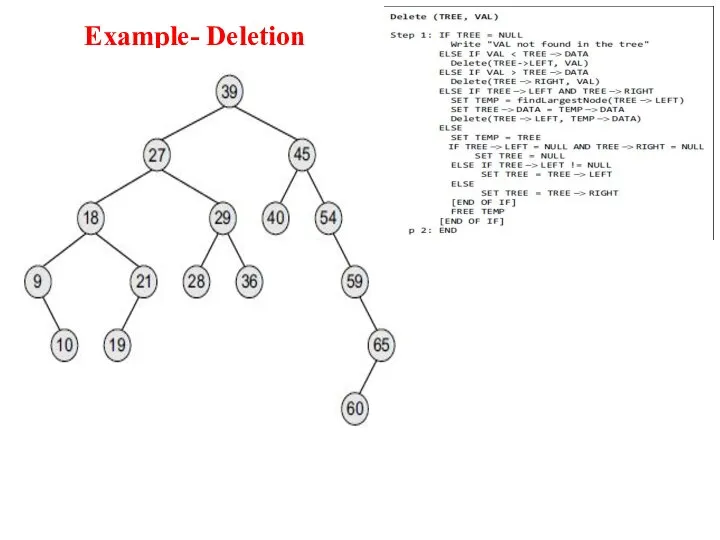
- 30. Example- Deletion
- 32. Скачать презентацию

















 Моря, омывающие берега России
Моря, омывающие берега России Образовательные технологии, содействующие сохранению здоровья учащихся
Образовательные технологии, содействующие сохранению здоровья учащихся Формування в учнів мислення, орієнтованого на стале майбутнє, в умовах інтеграційного простору навчально-виховного комплексу Чал
Формування в учнів мислення, орієнтованого на стале майбутнє, в умовах інтеграційного простору навчально-виховного комплексу Чал Digital environment
Digital environment оптимизация продаж Кирилл (2)
оптимизация продаж Кирилл (2) Современная живопись
Современная живопись Итоговое собрание. Students` business club
Итоговое собрание. Students` business club Система психологической и коррекционной работы тренера как условие адаптации к спортивной жизни
Система психологической и коррекционной работы тренера как условие адаптации к спортивной жизни Супрадин® Кидс Рыбки
Супрадин® Кидс Рыбки Применение международных и зарубежных стандартов в Российском авиастроении
Применение международных и зарубежных стандартов в Российском авиастроении Самостійна робота з судової риторики
Самостійна робота з судової риторики Неолиберализм, теория социального рыночного хозяйства
Неолиберализм, теория социального рыночного хозяйства  Памятники архитектуры. Витрины
Памятники архитектуры. Витрины Земля у нас одна!
Земля у нас одна! 24 декабря – день варежек
24 декабря – день варежек КОМПЛЕКСНО-ЦЕЛЕВАЯ ПРОГРАММА РАЗВИТИЯ«ГАЛАКТИКА-15»
КОМПЛЕКСНО-ЦЕЛЕВАЯ ПРОГРАММА РАЗВИТИЯ«ГАЛАКТИКА-15» Разноуровневое обучение как важное средство повышения качества преподавания иностранного языка
Разноуровневое обучение как важное средство повышения качества преподавания иностранного языка Традиции празднования Нового Года в разных странах
Традиции празднования Нового Года в разных странах Поведение потребителей
Поведение потребителей Мониторинг педагогического процесса в ДОУ
Мониторинг педагогического процесса в ДОУ Конструктивное исполнение линий электрипередачи (глава 3)
Конструктивное исполнение линий электрипередачи (глава 3) Строительная техника
Строительная техника Укрытия от непогоды из подручных материалов
Укрытия от непогоды из подручных материалов Презентация на тему Замечательные точки треугольника Свойство биссектрисы угла
Презентация на тему Замечательные точки треугольника Свойство биссектрисы угла  Военно-охотничье общество в настоящее время. Общероссийская спортивная общественная организация
Военно-охотничье общество в настоящее время. Общероссийская спортивная общественная организация Презентация на тему Архитектура и живопись в в XIV – XVI веках
Презентация на тему Архитектура и живопись в в XIV – XVI веках  Диетическое питание
Диетическое питание НИИ леса Финляндии
НИИ леса Финляндии