Вектор

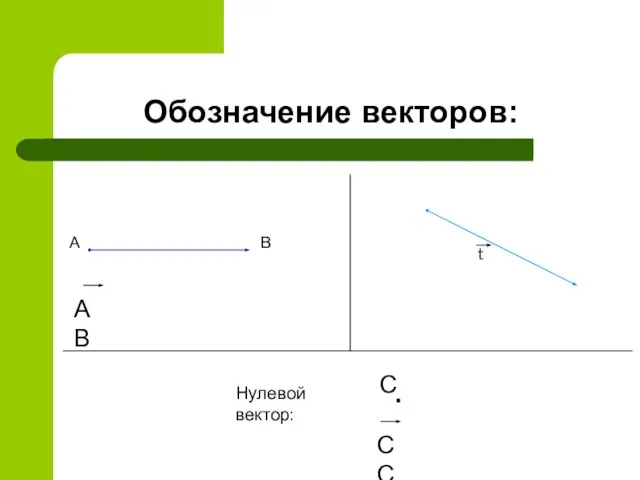
Обозначение векторов:
А
В
АВ
t
.
СС
С
Нулевой вектор:

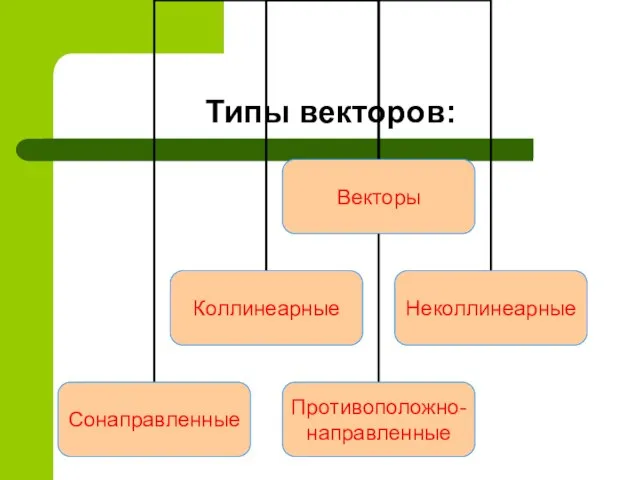
Типы векторов:

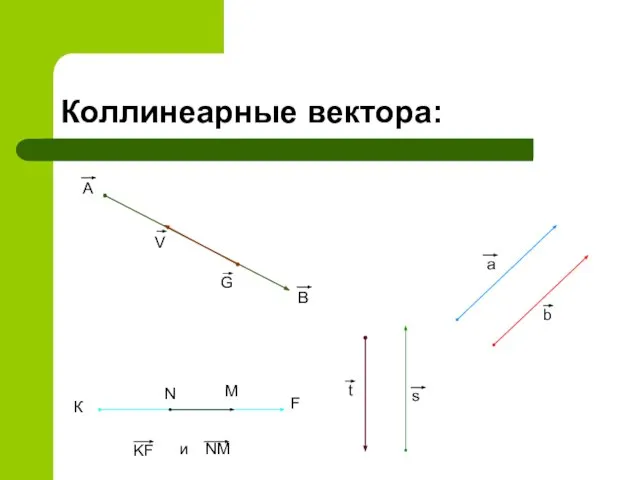
Коллинеарные вектора:
а
b
К
F
N
M
KF
и
NM
A
B
V
G
s
t

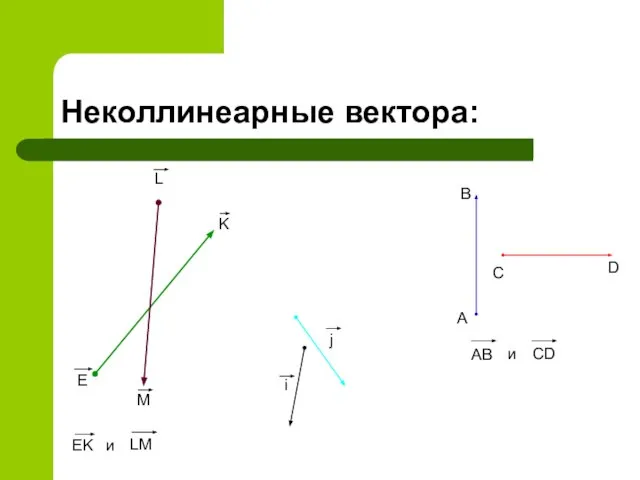
Неколлинеарные вектора:
А
В
С
D
AB
и
CD
E
K
L
M
EK
и
LM
j
i

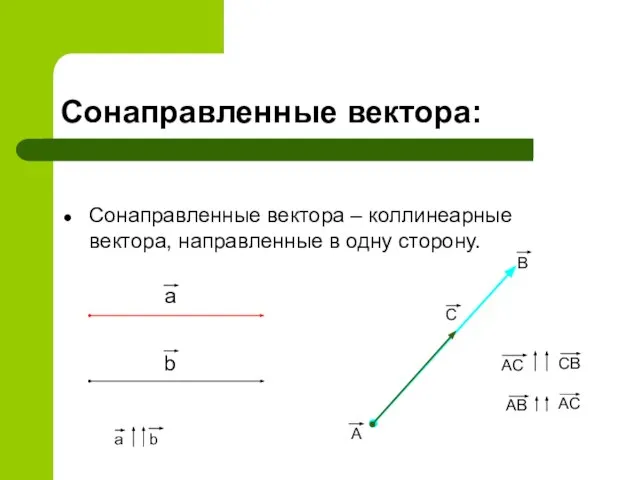
Сонаправленные вектора:
Сонаправленные вектора – коллинеарные вектора, направленные в одну сторону.
a
b
a
b
A
B
C
AC
CB
AB
AC

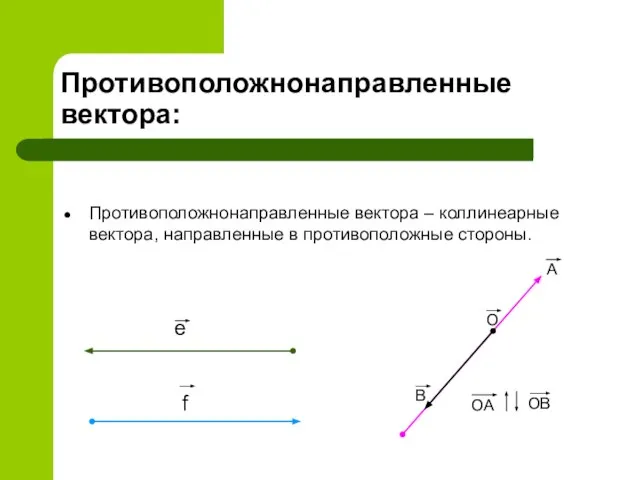
Противоположнонаправленные вектора:
Противоположнонаправленные вектора – коллинеарные вектора, направленные в противоположные стороны.
e
f
A
O
B
OA
OB

Сложение векторов

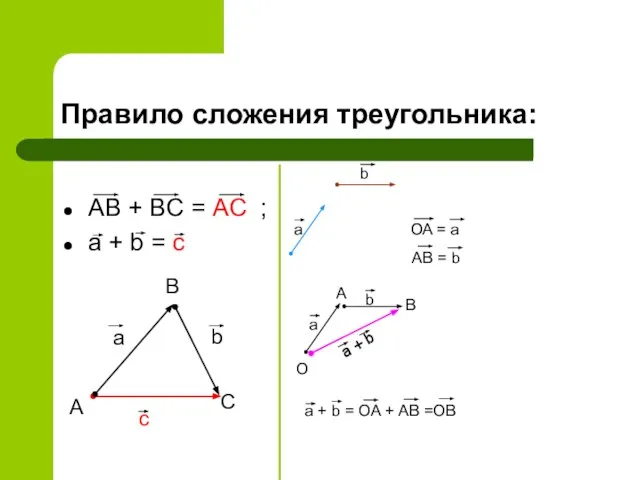
Правило сложения треугольника:
AB + BC = AC ;
a + b = c
a
b
c
A
B
C
a
b
OA = a
AB = b
O
A
B
a
b
a + b
a + b = OA + AB =OB

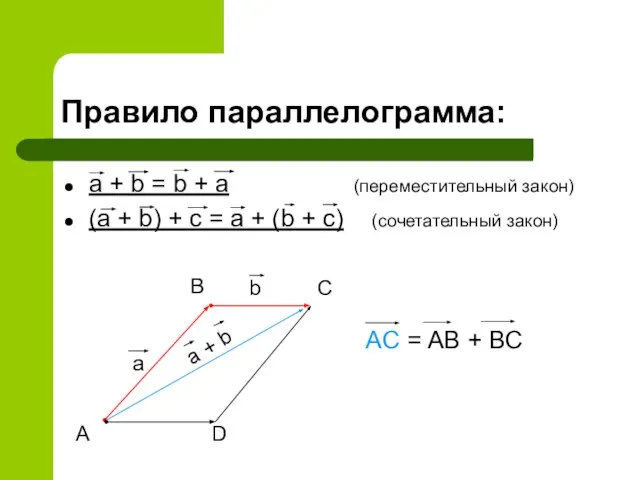
Правило параллелограмма:
a + b = b + a (переместительный закон)
(a + b) + c = a + (b + c) (сочетательный закон)
A
B
C
D
a
b
a + b
AC = AB + BC

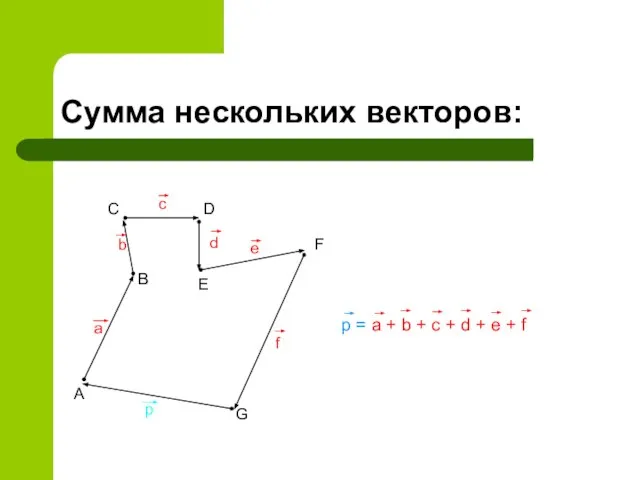
Сумма нескольких векторов:
A
B
C
D
E
F
G
a
b
c
d
e
f
p = a + b + c + d + e + f
p

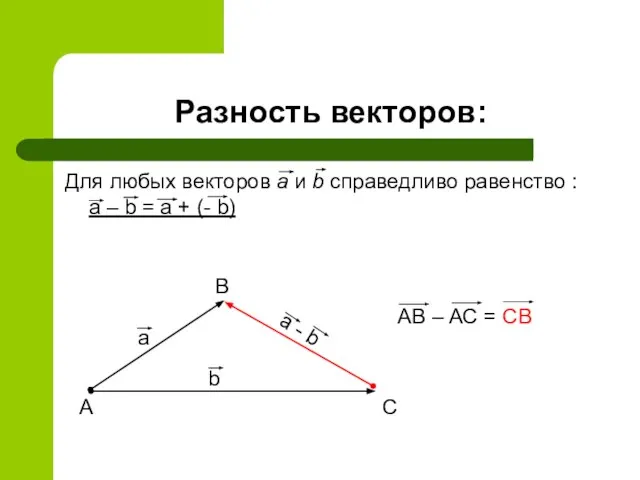
Разность векторов:
Для любых векторов a и b справедливо равенство : a – b = a + (- b)
A
B
C
a
b
a - b
AB – AC = CB

Умножение вектора на число:
(kl) • a = k • (la) (сочетательный закон)
(k + l) • a = ka + la (первый распределительный закон)
k (a + b) = ka + kb (второй распределительный закон)
k, l – числа ; a, b - вектора
a
b
c
b = 3a
c = -4a
b = ka, где k – число, a = 0
|b| = |k| • |a|
b a , если k > 0
b a , если k < 0