Векторные диаграммы.

Заполните таблицу
Механические величины
Электромагнитные величины

Добавьте соответствие
х макс
-х макс
I макс

Сделайте вывод
Что общего в механических и электромагнитных колебаниях:
А)природа;
В) законы, по которым они происходят.

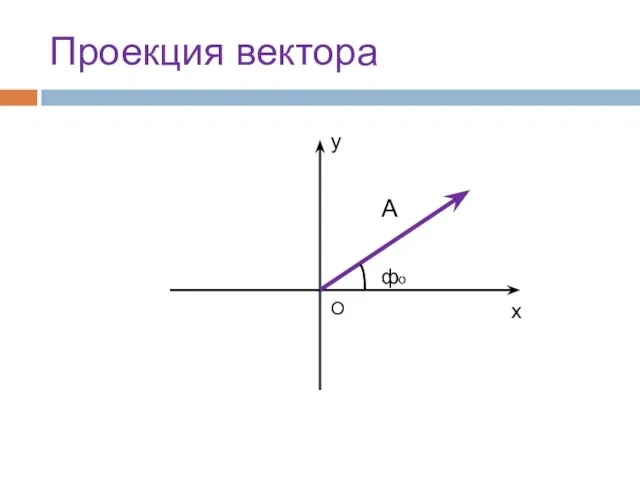
Проекция вектора
О
фо
А
у
х

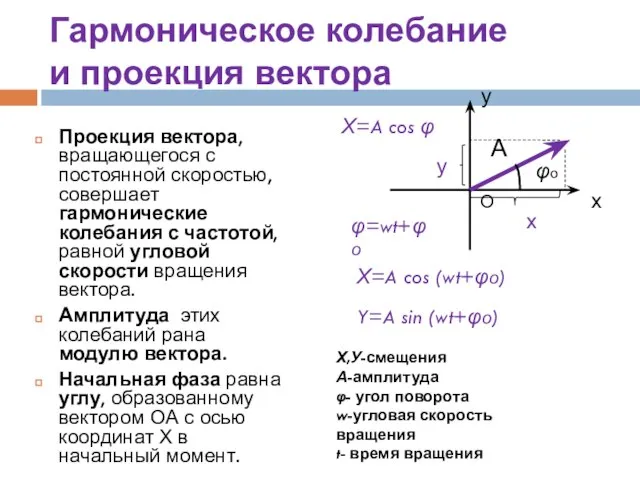
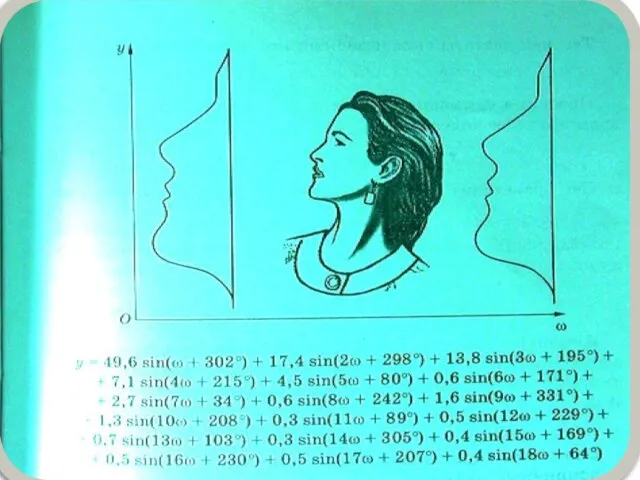
Гармоническое колебание
и проекция вектора
Проекция вектора, вращающегося с постоянной скоростью, совершает гармонические колебания с частотой, равной угловой скорости вращения вектора.
Амплитуда этих колебаний рана модулю вектора.
Начальная фаза равна углу, образованному вектором ОА с осью координат Х в начальный момент.
О
φо
А
у
х
Х=A cos (wt+φо)
φ=wt+φо
Х=A cos φ
Х,У-смещения
А-амплитуда
φ- угол поворота
w-угловая скорость вращения
t- время вращения
у
х
Y=A sin (wt+φо)

Определение
Векторной диаграммой называют графическое изображение гармонических колебаний и соотношений между гармонически колеблющимися величинами в помощью векторов.

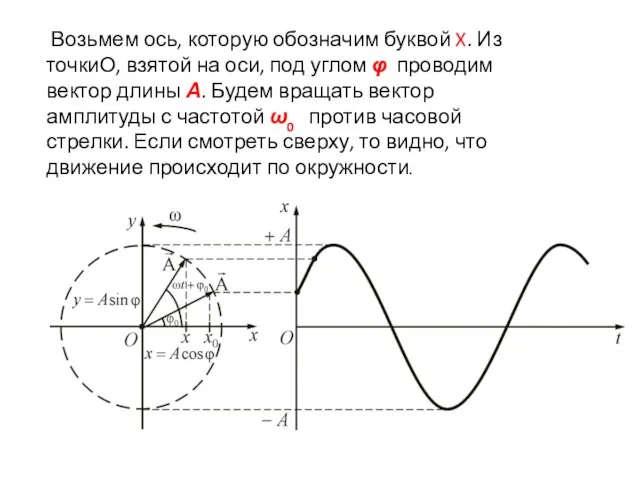
Возьмем ось, которую обозначим буквой X. Из точкиО, взятой на оси, под углом φ проводим вектор длины А. Будем вращать вектор амплитуды с частотой ω0 против часовой стрелки. Если смотреть сверху, то видно, что движение происходит по окружности.

Но человек, который смотрит “в торец” стола, наблюдает колебательное движение туда и обратно, по существу, он наблюдает проекцию кругового движения на ось X.
И это колебание проекции вектора амплитуды аналогично гармоническому колебанию.
X = Acos(ωt + φ) для x-проекция вектора-амплитуды .
Следовательно, проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.
Уравнение колебаний

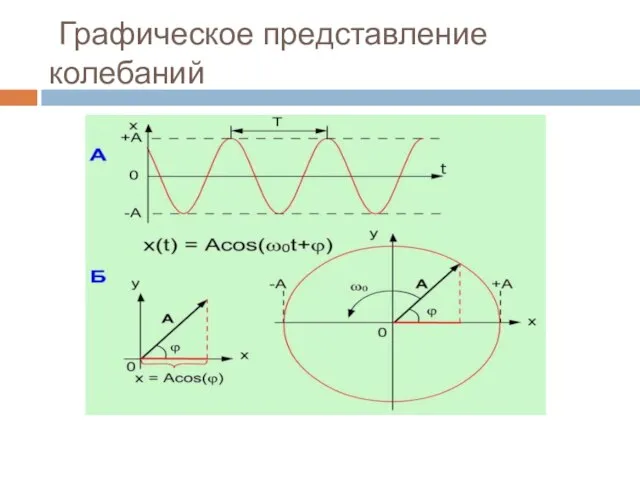
Графическое представление колебаний

Задание1
1. Построить векторную диаграмму гармонических электромагнитного колебаний заряда, тока, если
q=qo cos (wt+φо).

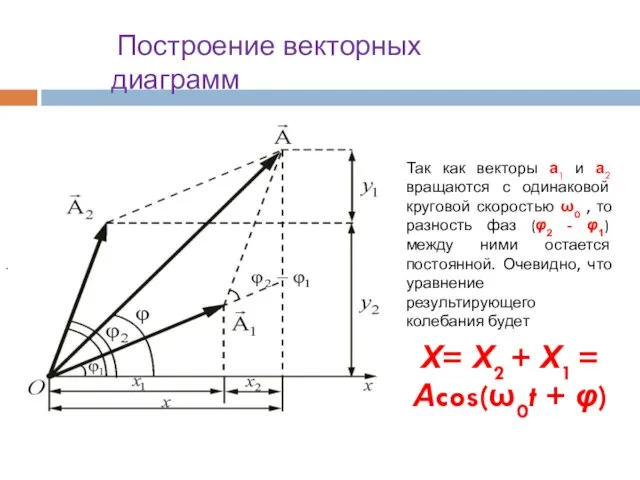
Сложение гармонических колебаний одинаковых частот
Сложение колебаний одинаковых частот проще всего осуществить с помощью так называемой векторной диаграммы.

Сложение гармонических колебаний одного направления и одинаковой частоты
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить.
Сложим гармонические колебания одного направления и одинаковой частоты.
Смещение Х колеблющегося тела будет суммой смещений Х1 и Х2, которые запишутся в следующим образом:
X 1= A1cos(ωt + φ01)
X 2= A2cos(ωt + φ02)
Представим оба колебания с помощью векторов а1 и а2. Построим по правилам сложения векторов результирующий вектор а

Так как векторы а1 и а2 вращаются с одинаковой круговой скоростью ω0 , то разность фаз (φ2 - φ1) между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет
Х= Х2 + Х1 = Аcos(ω0t + φ)
.
Рис. 25.3.
Построение векторных диаграмм

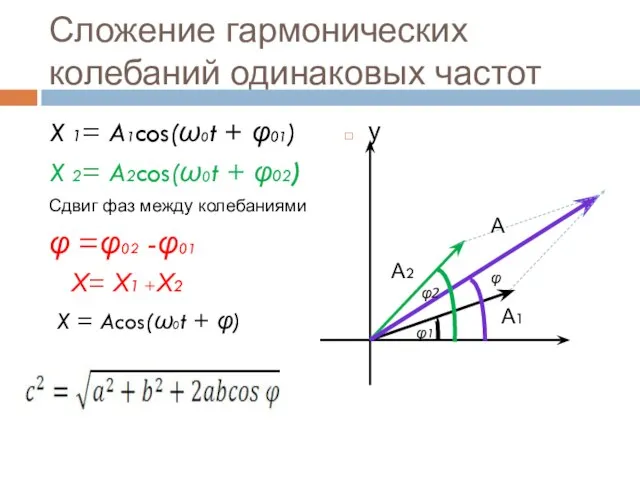
Сложение гармонических колебаний одинаковых частот
X 1= A1cos(ω0t + φ01)
X 2= A2cos(ω0t + φ02)
Сдвиг фаз между колебаниями
φ =φ02 -φ01
Х= Х1 +Х2
X = Acos(ω0t + φ)
у
А2
А1
А
φ1
φ
φ2

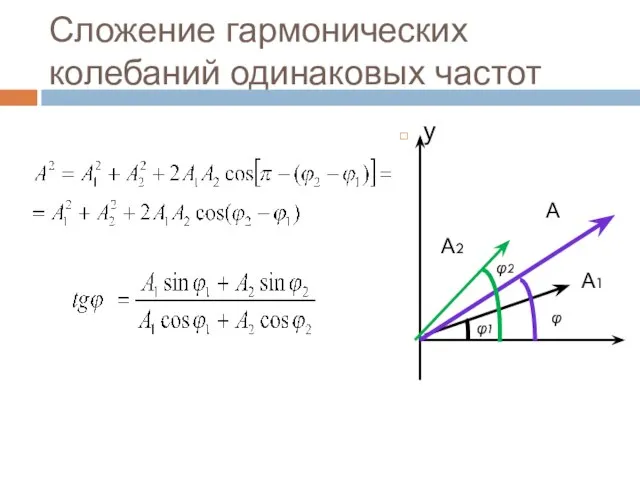
Сложение гармонических колебаний одинаковых частот
у
А2
А1
А
φ1
φ
φ2

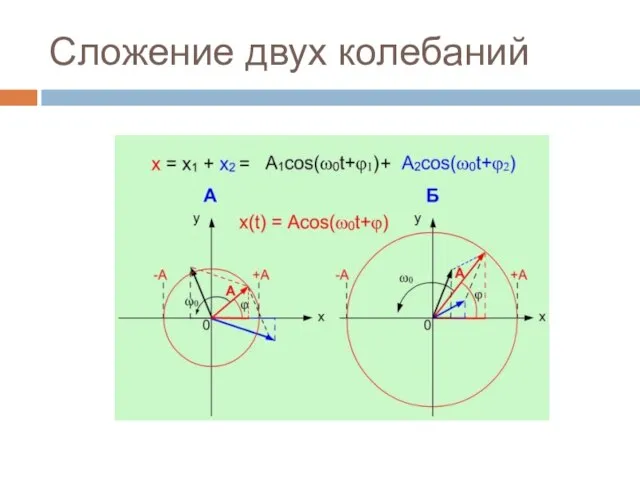
Сложение двух колебаний

Задание2
Сложить колебания:
q=qo sinwt
q=- 0.5 qo cos wt
q=-0.25 qo sinwt
q= 0.125 qo cos wt
Определить амплитуду и начальную фазу результирующего колебания

Применение
Векторная диаграмма широко применяются в электротехнике, акустике и оптике.