Содержание
- 2. Цель исследования: Узнать зависит ли существование правильного многогранника от количества вершин, рёбер и граней?
- 3. Задачи исследования: Научиться находить и извлекать необходимую информацию в условиях её обилия. Связать воедино теоретическую и
- 4. Гипотеза: Мы думаем, что в природе не существует больше пяти, известных нам, правильных многогранников.
- 5. План исследования: Правильные многогранники Применение теоремы Эйлера Теорема Эйлера
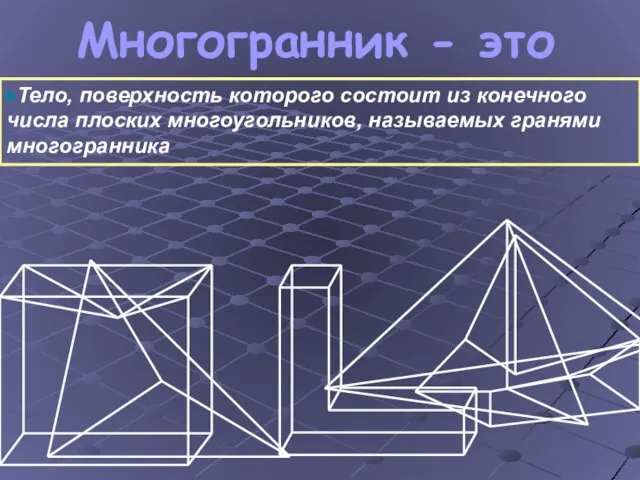
- 6. Многогранник - это Тело, поверхность которого состоит из конечного числа плоских многоугольников, называемых гранями многогранника
- 7. Выпуклый многогранник называется правильным, если: Его грани - правильные многоугольники В вершине сходится одно и то
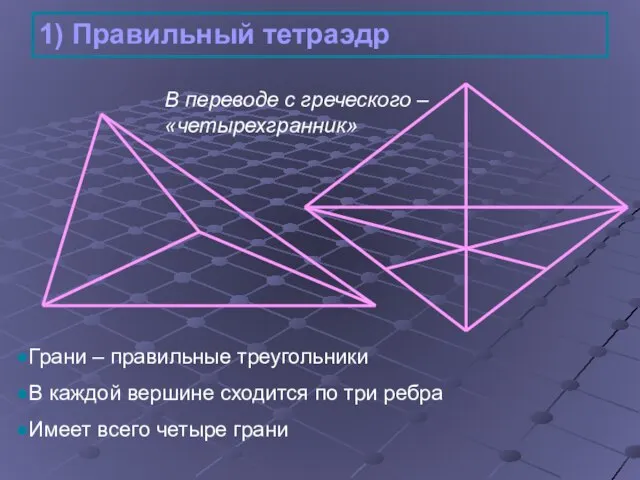
- 8. 1) Правильный тетраэдр Грани – правильные треугольники В каждой вершине сходится по три ребра Имеет всего
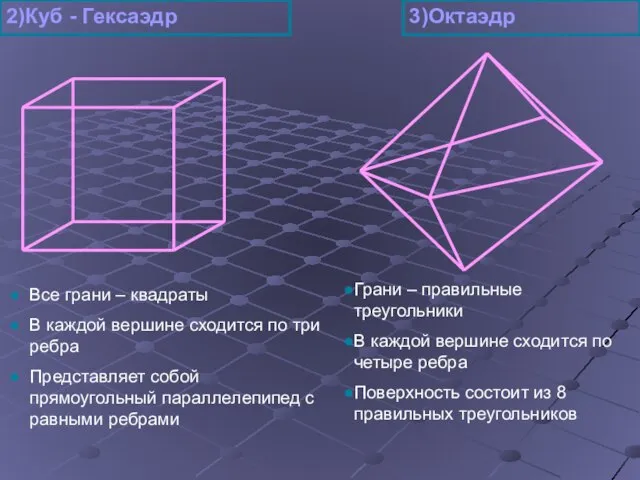
- 9. Все грани – квадраты В каждой вершине сходится по три ребра Представляет собой прямоугольный параллелепипед с
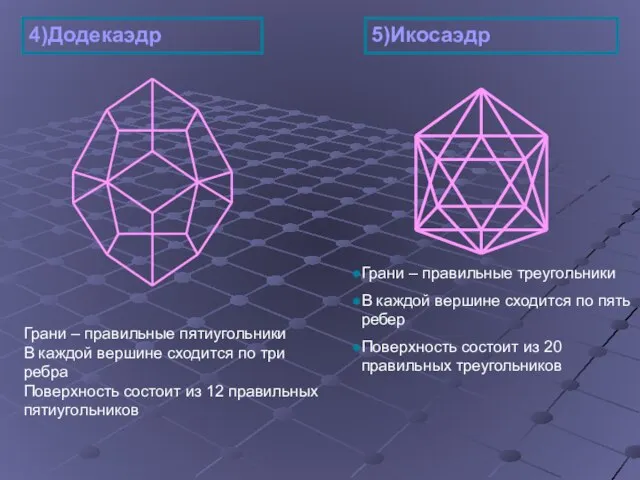
- 10. 4)Додекаэдр 5)Икосаэдр Грани – правильные треугольники В каждой вершине сходится по пять ребер Поверхность состоит из
- 11. Для любого выпуклого многогранника имеет место равенство В – Р + Г = 2 где В
- 12. Дан правильный многогранник: грани n-угольники, в вершине сходится m-рёбер. Ясно, что m,n больше или равны трём.
- 13. Содержание Вывод Используя теорему Эйлера, мы доказали, что в природе не существует больше пяти правильных многогранников.
- 15. Скачать презентацию








 Подготовка к ЕГЭ
Подготовка к ЕГЭ Животноводство России
Животноводство России Путешествие по сказочным тропинкам
Путешествие по сказочным тропинкам Молоко. Молочные продукты
Молоко. Молочные продукты Психолог в отделе полиции
Психолог в отделе полиции 24 апреля 1915 года младотурецкие правители Талаат-паша, Энвер-паша и Джемаль-паша — приказали собрать всю армянскую интеллигенцию в
24 апреля 1915 года младотурецкие правители Талаат-паша, Энвер-паша и Джемаль-паша — приказали собрать всю армянскую интеллигенцию в Программа строительства и реконструкции котельных муниципальных образований Московской области - приоритетный инвестиционный п
Программа строительства и реконструкции котельных муниципальных образований Московской области - приоритетный инвестиционный п Глобальный экологический университет (по улучшению качества жизни)
Глобальный экологический университет (по улучшению качества жизни) Оформление чертежа
Оформление чертежа ЕДИНАЯ ИНТЕЛЛЕКТУАЛЬНАЯ СИСТЕМА УПРАВЛЕНИЯ И АВТОМАТИЗАЦИИ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ НА ЖЕЛЕЗНОДОРОЖНОМ ТРАНСПОРТЕ (ИСУЖТ)
ЕДИНАЯ ИНТЕЛЛЕКТУАЛЬНАЯ СИСТЕМА УПРАВЛЕНИЯ И АВТОМАТИЗАЦИИ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ НА ЖЕЛЕЗНОДОРОЖНОМ ТРАНСПОРТЕ (ИСУЖТ) Ландшафтный дизайн и озеленение участка
Ландшафтный дизайн и озеленение участка Кальянные миксы. Обеспечь себе истинное наслаждение
Кальянные миксы. Обеспечь себе истинное наслаждение Презентация на тему Логические операции
Презентация на тему Логические операции Хатеновская Елена Васильевна
Хатеновская Елена Васильевна SK700-II (Sandpiper II Electronics)
SK700-II (Sandpiper II Electronics) Духовная сфера общества. Религия
Духовная сфера общества. Религия Equalizer
Equalizer XIII Международная конференция "Маркетинг в России" Сообщение: «ОСОБЕННОСТИ ОНЛАЙН ИССЛЕДОВАНИЙ В РОССИИ» Александр Шашкин (Online Market
XIII Международная конференция "Маркетинг в России" Сообщение: «ОСОБЕННОСТИ ОНЛАЙН ИССЛЕДОВАНИЙ В РОССИИ» Александр Шашкин (Online Market  Здравствуй, милая картошка!
Здравствуй, милая картошка! ИСТОРИЯ РОССИИ
ИСТОРИЯ РОССИИ Полисахариды
Полисахариды Презентация на тему Труд земной. Ремесла на Руси
Презентация на тему Труд земной. Ремесла на Руси Saxotech 170
Saxotech 170 Внешняя политика СССР
Внешняя политика СССР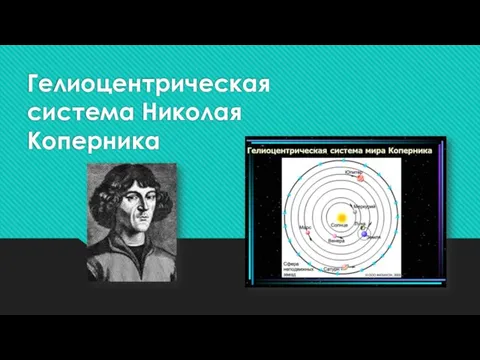 Гелиоцентрическая система Николая Коперника
Гелиоцентрическая система Николая Коперника Шираб-Жамсо Раднаев
Шираб-Жамсо Раднаев «Давньогрецька міфологія як основа формування філософії та розвитку Європейської цивілізації в цілому»
«Давньогрецька міфологія як основа формування філософії та розвитку Європейської цивілізації в цілому» Их лик сияет над Симбирском
Их лик сияет над Симбирском