Великие математики и их исследования

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Задачи
Головоломки
Великие
математики

ВЕЛИКИЕ МАТЕМАТИКИ
Фалес 625-548 год до н.э
Фалес – это первый древнегреческий мыслитель. Фалес известен тем, что ввел в геометрию доказательства. Он начал строить геометрию на логических основаниях, постепенно переходя при помощи доказательств от одного положения к другому.
Фалесу Милетскому приписывают простой способ определения высоты пирамиды. В солнечный день он поставил свой посох там, где оканчивалась тень от пирамиды. Затем он показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха.
Вот теорема Фалеса:
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его сторон.
Фалес

ВЕЛИКИЕ МАТЕМАТИКИ
ПИФАГОР 570 – 496 г. до н.э.
Великий древнегреческий ученый. Родился на острове Самос около 570 г. до н.э.
«Пифагоровы штаны» (школьн. устар.) - шуточное название теоремы Пифагора, возникшее в силу того, что раньше в школьных учебниках эта теорема доказывалась через равенство суммы площадей квадратов, построенных на катетах прямоугольного треугольника; площади квадрата, построенного на гипотенузе этого треугольника.
В настоящее время установлено, что эта важнейшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора.
Верёвочным треугольником со сторонами 3, 4 и 5 единиц пользовались ещё в Древнем Египте. Поэтому треугольник со сторонами 3, 4 и 5 называют ещё иногда египетским.
Пифагор

ВЕЛИКИЕ МАТЕМАТИКИ
РЕНЕ ДЕКАРТ 1596 - 1650
Математические исследования Декарта связаны с его работами по философии и физике. В "Геометрии" (1637) Декарт впервые ввёл понятия переменной величины и функции.
Декартова система координат - система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям - прямоугольные декартовы координаты.
Рене Декарт

ВЕЛИКИЕ МАТЕМАТИКИ
ГЕОРГ КАНТОР
Родился в Петербурге. В 1867 окончил Берлинский университет. Кантор разработал теорию бесконечных множеств и теорию трансфинитных чисел. В 1874 он доказал несчётность множества всех действительных чисел, установив существование неэквивалентных (т. е. имеющих разные мощности) бесконечных множеств, сформулировал (в 1878 году) общее понятие мощности множества. С 1879 по 1884 Кантор изложил принципы своего учения о бесконечности. Идеи оказали большое влияние на развитие математики.
Георг Кантор

ВЕЛИКИЕ МАТЕМАТИКИ
Гаусс Карл Фридрих (30.4.1777-23. 2. 1855 )
Иоганн Фридрих Карл Гаусс родился 30 апреля 1777г. С трех лет он уже умел считать и выполнять вычисления. Однажды, при расчетах отца, который был водопроводным мастером, трехлетний Гаусс заметил ошибку в вычислениях. Расчет был проверен, и число, указанное мальчиком было верно. В 1784г. Карл пошел в школу. Учитель очень заинтересовался маленьким Гауссом.
Гаусс Карл Фридрих

ЗАДАЧИ
Задачи на совместную работу изучают с 4 по 7 класс. Всю работу принимают за одно целое – единицу. Рассмотрим это на примере простейшей задачи:
Кошка может поймать за 3 дня 9 мышей. Какова производительность ловли кошки?
9 мышек мы принимаем за единицу, так как это вся работа, которую выполняет кошка за 3 дня.
Задачи на совместную работу

ЗАДАЧИ
Производительность – часть работы, выполняемая кем-либо за 1 день.
Вот ты и узнал первое правило. Все правила я буду выделять красным цветом и подчеркивать, а ты не забывай вносить их в свой словарик.
Итак, вернёмся к задаче. Чтобы найти производительность ловли кошки, разделим число пойманных мышек на количество затраченных дней.
1) 9 : 3 = 3 (мышки в день
производительность ловли кошки)
Задачи на совместную работу

ЗАДАЧИ
Теперь рассмотрим более сложную задачу:
2 пони: виллийский и шетландский перевозят в тележке детей. Виллийский пони способен перевезти всех детей за 6 часов, а шетландский в 2 раза быстрее. За какое время они справятся с этой работой, если будут работать вместе?
Задачи на совместную работу

В этой задаче нужно сначала найти производительность виллийского пони, затем шетланского и найти сумму их производительности. А всю работу (1) разделить на полученный результат.
1) 6 : 2 = за 3 (часа перевозит детей шетландский пони)
2) 1 : 6 = (часть детей перевезёт за 1 час виллийский пони)
3) 1 : 3 = (часть детей перевозит за 1 час шетландский пони)
4) + = (часть детей перевозят за 1 час два пони)
5) 1 : = 2 ( часа они управятся с этой работой)
Думаю, что с задачами на совместную работу мы разобрались и смело можем переходить к следующему разделу.
Задачи на совместную работу
ЗАДАЧИ

ЗАДАЧИ
В основном, задачи на движение решают по формулам:
t х v = S; S : t = v, S : v = t где
S – расстояние
t – время
v – скорость
Собаке нужно пробежать 32 километра за 2 часа. Какова скорость собаки?
Задачи на движение

ЗАДАЧИ
Запиши формулы в свой словарик. Я надеюсь, что они помогут тебе решить мою задачу.
1) 32 : 2 = 16 (километров в час скорость собаки)
Теперь познакомимся с задачей посложнее.
Кошка, находясь от собаки в 32 километрах, по ошибке бежит ей навстречу со скоростью 6 километров в час. Скорость собаки 10 километров в час. Через какое время кошка может остаться без хвоста?
Задачи на движение

ЗАДАЧИ
В этой задаче ты столкнулся с величиной – время сближения. Время сближения – это время через которое произойдет сближение.
Твой словарик пора пополнить. Запиши в него это понятие.
Найди скорость сближения кошки и собаки, а затем расстояние между этими закадычными врагами подели на их скорость сближения.
Задачи на движение

ЗАДАЧИ
1) 6 + 10 = 16 (километров в час скорость сближения) 2) 32 : 16 = через 2 (часа кошка останется без хвоста)
Давай ты передохнёшь, и мы начнём разбирать следующую задачу.
Задачи на движение

ЗАДАЧИ
Два вредных кота поссорились и разбежались в разные стороны. Скорость Забияки 6 километров в час, скорость Задиры ­– в 1,2 раза больше. Через какое время расстояние между ними будет 26,4 километра?
Здесь присутствует время удаления.
Время удаления – это время, по прошествии которого объекты находятся друг от друга на определённом расстоянии.
Запиши этот термин в свой словарик.
Задачи на движение

ЗАДАЧИ
Узнай скорость кота Задиры, найди скорость сближения и раздели 26,4 километра на полученный результат .
1) 6 х 1,2 = 7,2 (километра в час скорость Задиры)
2) 6 + 7,2 = 13,2 (километра в час скорость сближения)
3) 26,4 : 13,2 = 2 (часа коты будут на расстоянии 26,4 километров друг от друга)
Остался один вид задач на движение, и мы перейдём к следующему разделу.
Задачи на движение

ЗАДАЧИ
Пчела Майя вылетела из улья со скоростью 12 километров в час. Через часа из этого же улья вылетела пчела Июлия и догнала Майю через 0,5 часа. Какова скорость Июлии?
В этой задаче присутствует движение вдогонку.
Движение вдогонку – это вид движения, во время которого один объект (чаще всего с большей скоростью) догоняет другой.
Запиши новое правило в свой словарик.
Задачи на движение

ЗАДАЧИ
Найди, какое расстояние пролетела Майя за часа и прибавь расстояние, которое Майя пролетела за 0,5 часа. Исходя из полученных данных, узнай какое расстояние пролетает за час Июлия.
1) 12 х = 4 (километра пролетела Майя за часа)
2) 12 х 0,5 = 6 (километров пролетела Майя за 0,5 часа)
3) 4 + 6 = 10 (километров пролетает Июлия за 0,5 часа)
4) 10 : 0,5 = 20 (километров в час скорость Июлии)
Задачи на движение

ЗАДАЧИ
Последний тип задач на движение – задачи на движение по реке.
Ёж плывёт по реке со скоростью 1,5 километра в час. Скорость течения 2 километра в час. Какое расстояние проплывёт ёж за 3 часа?
Чтобы решить эту задачу, я предлагаю тебе воспользоваться формулой:
(v теч. + v объекта) х t = S, где
v - скорость
t – время
S - расстояние
Задачи на движение

ЗАДАЧИ
Вот решение этой задачи:
1) 1,5 + 2 = 3,5 (километра в час скорость ежа по течению реки)
2) 3,5 х 3 = 10,5 (километров проплывёт ёж)
А вот тебе еще задача:
Выдра плывет по реке против течения. Скорость выдры 40 километров в час, а скорость реки – 5 километров в час. Какое расстояние преодолеет выдра за 5 часов?
Задачи на движение

ЗАДАЧИ
Здесь уже другая формула, поэтому её тоже следует записать.
(v объекта - v теч.) х t = S, где
v - скорость
t – время
S - расстояние
А вот и решение:
1) 40 – 5 = 35 (километров в час скорость выдры против течения реки)
2) 35 х 5 = 175 (километров проплывет выдра)
Вот мы и закончили этот раздел. Пора переходить к следующему.
Задачи на движение

ЗАДАЧИ
Новая тема – задачи на проценты.
Процент – это одна сотая часть от числа.
Чтобы решить задачу на проценты, надо перевести их в десятичную дробь. (20% - 0,2, 75% - 0,75 и т.д.)
Вот пример одной из этих задач.
В малиннике росло 138 ягод. Медведь съел
50% ягод. Сколько ягод съел медведь?
Здесь нужно найти процент от числа.
Чтобы найти процент от числа, надо это
число умножить на десятичную дробь.
Задачи на проценты

ЗАДАЧИ
Надеюсь ты внес в свой словарик новые правила. Теперь ты понял как решить эту задачку?
50% - 0,5
1) 138 х 0,5 = 69 (ягод съел медведь)
Задачи на проценты бывают двух видов - на нахождение процента от числа и на нахождение числа по проценту. Первый вид задач мы уже изучили и сейчас приступим ко второму.
Задачи на проценты

ЗАДАЧИ
Птенцы съели 8 червяков, что составляет 75% от всех червяков. Сколько червяков у птенцов?
Чтобы найти число по проценту, надо его часть разделить на процент.
Теперь приступим к решению задачи.
75% - 0,75
1) 8 : 0,75 = 12 (червяков было у птенцов)
Ты быстро учишься! Вот уже и закончился раздел «Задачи н проценты». Поздравляю.
Задачи на проценты

ЗАДАЧИ
Теперь мы будем изучать задачи на части.
У лисы 5 лисят. Она накормила 1/5 часть всех лисят. Сколько лисят накормила лиса?
Чтобы найти часть от числа, надо число умножить на эту часть.
Я думаю, ты догадался, как решать эту задачку. Я покажу тебе своё решение.
Задачи на части

ЗАДАЧИ
5 х 1
5
1)5 х 1/5 = 1 (лисенка накормила лиса) А теперь изучим второй вид этого типа задач.
У зайчихи несколько зайчат. Известно, что 8 зайчат составляют 1/4 часть всех зайчат. Сколько зайчат у зайчихи?
Чтобы найти число по его части, надо данное число разделить на часть.
Сверь своё решение с моим.
1) 8 : 1/4 = 32 (зайчонка у зайчихи)
У нас остался самый сложный вид задач – задачи на пропорции.
Задачи на части

ИСТОРИЧЕСКАЯ СПРАВКА
Судоку
ЧТО ТАКОЕ «СУДОКУ»?

ГОЛОВОЛОМКИ
Привет, мой любознательный друг! Я решила познакомить тебя с СУДОКУ. Сейчас я поведаю тебе о том, что же это такое.
Судоку придумал в 1979 году Ховард Гарнс, 74-летний американский архитектор, который увлекался конструированием головоломок; он назвал свои головоломки «Размещение цифр». Игра получила название «судоку» в Японии (су – число, доку – единственный), где появилась в 1980-х годах благодаря издателю головоломок Николи.
Однако настоящие корни судоку уходят в 1780-е годы, когда математик Леонард Эйлер придумал свои «латинские квадраты», которые в свою очередь происходят от «магических квадратов» (с ними мы познакомимся позже).
Судоку

ГОЛОВОЛОМКИ
Теперь я расскажу тебе правила игры.
Итак, правила судоку очень просты. Ты заполняешь поле 9х9 таким образом, чтобы каждая строка, колонка и блок 3х3 содержали все цифры от 1 до 9. Цифры не должны повторяться в какой-либо строке, колонке или блоке, и ни одна цифра не может быть пропущена. Каждая головоломка начинается с нескольких цифр, размещенных на поле, а цель игры – заполнение всех пустых клеток поля.
Судоку

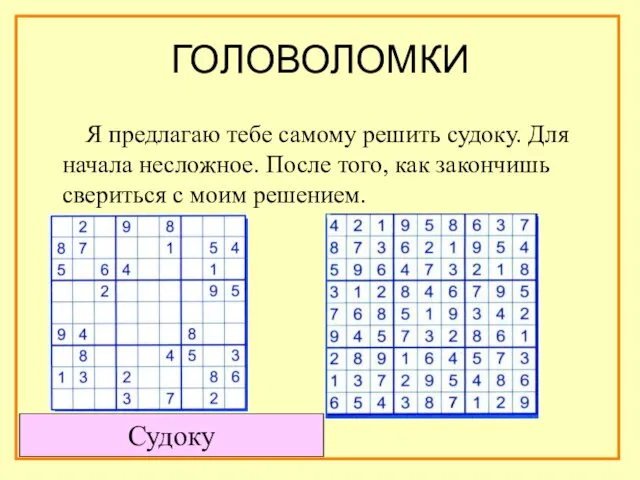
ГОЛОВОЛОМКИ
Я предлагаю тебе самому решить судоку. Для начала несложное. После того, как закончишь свериться с моим решением.
Судоку

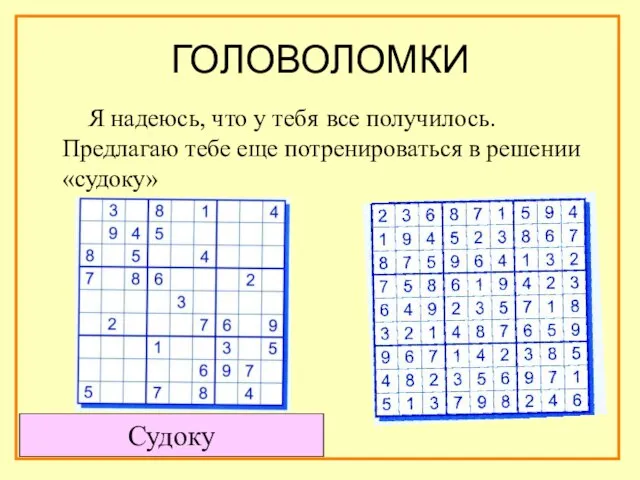
ГОЛОВОЛОМКИ
Я надеюсь, что у тебя все получилось. Предлагаю тебе еще потренироваться в решении «судоку»
Судоку

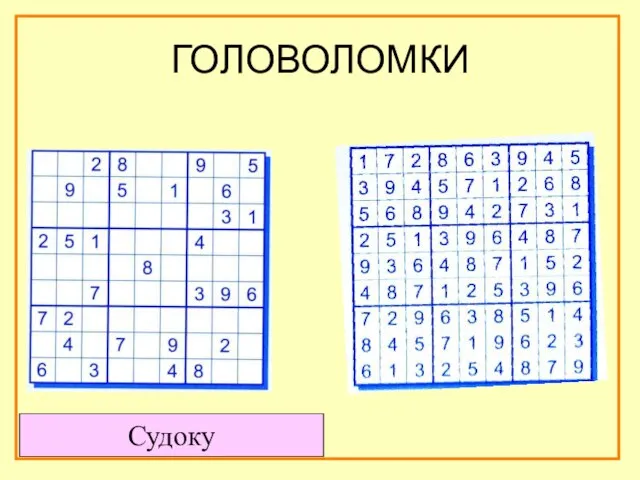
ГОЛОВОЛОМКИ
Судоку

ИСТОРИЧЕСКАЯ СПРАВКА
ЧТО ТАКОЕ «МАГИЧЕСКИЙ КВАДРАТ»?
Магический квадрат

ГОЛОВОЛОМКИ
Ну что ж, давай я подробнее расскажу о магических квадратах.
Магические квадраты- удивительные представители воображаемого мира чисел. Магическим квадратом n- го порядка называется квадратная таблица размером n × n, заполненная натуральными числами от 1 до n², суммы которых по всем строкам, столбцам и обеим диагоналям одинаковы. Различают магические квадраты четного и нечетного порядка. Поля таблицы, в которые записывают числа, называются клетками магического квадрата, а сумму чисел, стоящих в любой строке, столбце или на диагонали,- его постоянной.
Магический квадрат

ГОЛОВОЛОМКИ
Теперь посмотри, как заполнить магический квадрат. Магические квадраты возникли в глубокой древности в Китае. Вероятно, самым «старым» из дошедших до нас магических квадратов является таблица Ло шу. Она имеет размер 3 × 3 и заполнена натуральными числами от 1 до 9. В этом квадрате сумма чисел в каждой строке, столбце, диагонали равна 15. Для начала представим число 15 в виде сумм троек натуральных чисел от 1 до 9. Получим следующие восемь комбинаций.
1+5+9 2+6+7
1+6+8 3+4+8
2+4+9 3+5+7
2+5+8 4+4+6
Теперь тройки чисел надо разместить соответ­ствующим образом в клетках квадрата. Замечаем, что число 5 входит сразу в четыре суммы. Зна­чит, содержащая его клетка должна находиться на пересечении четырех прямых рядов. В квадра­те размером 3×3 этому условию удовлетворяет только одна клетка – центральная. Название «магические» квадраты получили от арабов, которые усмотрели в их свойствах нечто мистическое и поэтому принимали квадраты за своеобразные талисманы, защищавшие тех, кто их носит, от многих несчастий.
Магический квадрат

ГОЛОВОЛОМКИ
Квадрат Дюрера имеет размер 4 × 4 и составлен из шестнадцати первых натуральных чисел, сумма которых в каждой строчке, столбце и по диагонали равна 34. Оказалось, 34-м равны и суммы других четверок чисел: расположенных в центре, в угловых клетках, по бокам центрального квадрата, а также образующих четыре равных квадрата, на которые можно разделить исходный квадрат. А вот числа 15 и 14 в нижней
строке квадрата указывают дату создания
гравюры-1514 г.
Магический квадрат

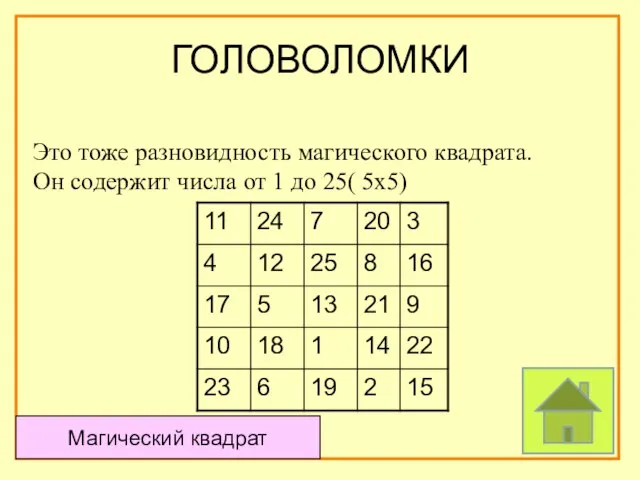
ГОЛОВОЛОМКИ
Это тоже разновидность магического квадрата. Он содержит числа от 1 до 25( 5х5)
Магический квадрат
Магический квадрат

САМОСТОЯТЕЛЬНАЯ РАБОТА
Пожалуйста, выбери вариант, который ты будешь выполнять.
Самостоятельные работы
1 вариант
2 вариант

САМОСТОЯТЕЛЬНАЯ РАБОТА
ЗАДАНИЕ 1
Котёнок гулял на расстоянии 24 километров от дома. Мама-кошка решила пойти к нему и двинулась со скоростью 18 километров в час. Через какое время мама найдёт своего непослушного котёнка?
1 вариант

1 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА
Сравни свое решение с моим.
24 : 18 = 1час 20 минут
Если у тебя такое же решение ты получаешь 5 баллов. Если у тебя ошибка ты получаешь 0 баллов.

САМОСТОЯТЕЛЬНАЯ РАБОТА
ЗАДАНИЕ 2
У кенгуру родилось 8 кенгурят, что составляет 1/8 часть всех кенгурят, родившихся летом. Сколько кенгурят родилось летом?
1 вариант

САМОСТОЯТЕЛЬНАЯ РАБОТА
Сделай проверку!
8 : 1/8 = 64 (кенгуренка родилось летом)
Не забывай дописывать при правильном решении по 5 баллов в свой дневничок.
1 вариант

САМОСТОЯТЕЛЬНАЯ РАБОТА
ЗАДАНИЕ 3
Число тараканов, живущих в доме сначала увеличилось на 10%, а затем уменьшилось на 10% . Сколько тараканов проживает в доме сейчас, если известно, что изначальноих число достигло 100?
1 вариант

САМОСТОЯТЕЛЬНАЯ РАБОТА
А теперь нужно выполнить проверку.
100 х 0,1 = 10 (тараканов составляют 10%)
100 + 10 = 110 (тараканов стало после увеличения их численности)
110 х 0,1 = 11 (тараканов составляют 10% от 110)
110 – 11 = 99 (тараканов выжило)
1 вариант

САМОСТОЯТЕЛЬНАЯ РАБОТА
ЗАДАНИЕ 4
Совенок за 24 ночи может поймать 48 мышек. Ему в помощь прилетел второй совенок, который может поймать столько же мышек за 12 ночей. За сколько ночей совята, работая вместе, поймают 48 мышек?
1 вариант

1 вариант
Проверь своё решение по моему:
48 : 24 = 2 ( мыши в ночь ловит первый совёнок)
48 : 12 = 4 (мыши в ночь ловит второй совенок)
2 + 4 = 6 (ночей)
Если у тебя такое же решение смело прибавляй себе ещё 5 баллов, а если нет – не прибавляй ничего.
САМОСТОЯТЕЛЬНАЯ РАБОТА

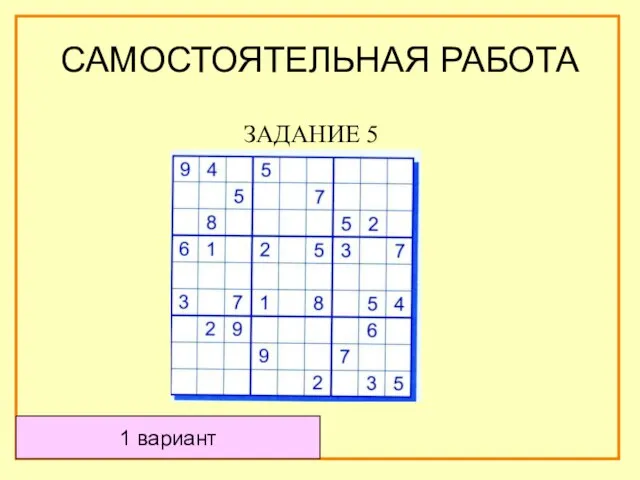
САМОСТОЯТЕЛЬНАЯ РАБОТА
ЗАДАНИЕ 5
1 вариант

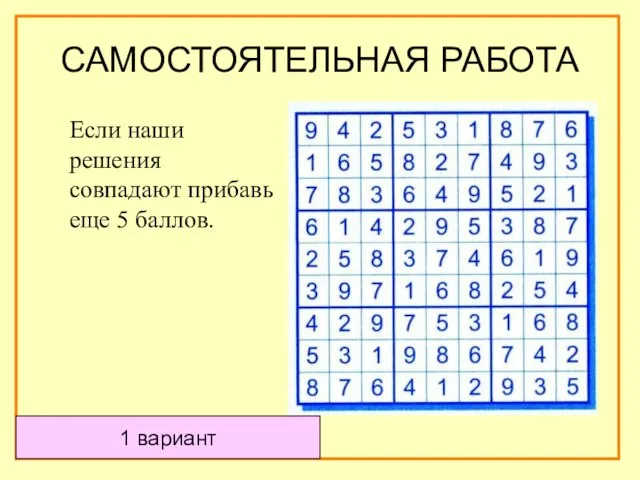
САМОСТОЯТЕЛЬНАЯ РАБОТА
1 вариант
Если наши решения совпадают прибавь еще 5 баллов.

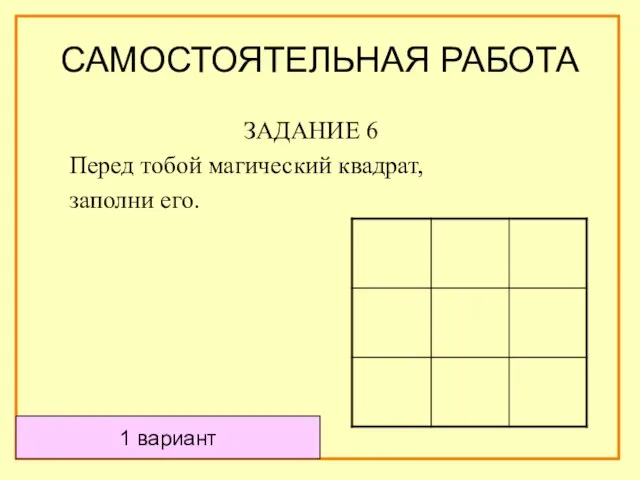
САМОСТОЯТЕЛЬНАЯ РАБОТА
ЗАДАНИЕ 6
Перед тобой магический квадрат,
заполни его.
1 вариант

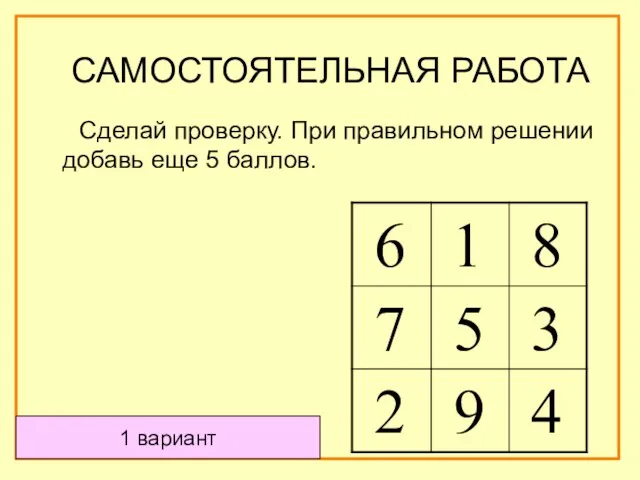
Сделай проверку. При правильном решении добавь еще 5 баллов.
1 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

Подведём итоги. Если ты набрал
от 30 до 25 баллов - ты заработал 5;
от 20 до 10 баллов – твоя оценка 4;
5 баллов – у тебя 3,
но, а если ты не набрал ни одного балла не отчаивайся и попробуй решить задания еще раз. Я уверена, что у тебя все получится.
1 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

2 вариант
ЗАДАНИЕ 1
Сорока полетела к своей подруге со скоростью 15 километров в час. Известно, что она прилетела к ней через 2 часа 30 минут. Каково расстояние между подругами?
САМОСТОЯТЕЛЬНАЯ РАБОТА

2 вариант
Проверь своё решение.
15 х 2,5 = 37,5 (километра)
Надеюсь, что у тебя такое же решение, тогда ты получишь 5 баллов, а если нет – останешься ни с чем.
САМОСТОЯТЕЛЬНАЯ РАБОТА

ЗАДАНИЕ 2
Черепаха отложила в кладку 15 яиц. Когда черепашки вылупились, они поползли к воде. Всего до воды доползло 12 черепашек. Какую часть составляют черепашки, добравшиеся до воды, от всех вылупившихся черепашек?
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

Выполни проверку.
1) 12 : 15 = 4/5 (части всех черепах добрались до воды)
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

ЗАДАНИЕ 3
У зебры Анны 60 полосок, у ее сестры Иры на 50% меньше полосок, а у ее подруги Надежды полос на 10% больше, чем у Иры. Сколько полосок у Надежды?
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

Надеюсь наши решения совпали…
60 х 0,5 = на 30 (полосок у Иры меньше)
60 – 30 = 30 (полосок у Иры)
30 х 0,1 = на 3 (полоски у Надежды больше)
30 + 3 = 33 (полоски у Надежды)
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

2 вариант
ЗАДАНИЕ 4
Утёнок за 3 дня откопал 12 червячков, а цыпленок за это же время откопал 6 червячков. Сколько червячков поймают птички за 3 дня?
САМОСТОЯТЕЛЬНАЯ РАБОТА

Ну-ка сделай проверку!
12 : 3 = 4 (червячка откапывает за день утенок)
6 : 3 = 2 (червячка откапывает за день цыпленок)
4 + 2 = 6 (червячков откапывают за день оба птенца)
6 х 3 = 18 (червячков откапают птенцы за 3 дня)
Если ты решил задачку правильно подпиши себе еще 5 баллов, а если нет то и подписывать к сожалению нечего.
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

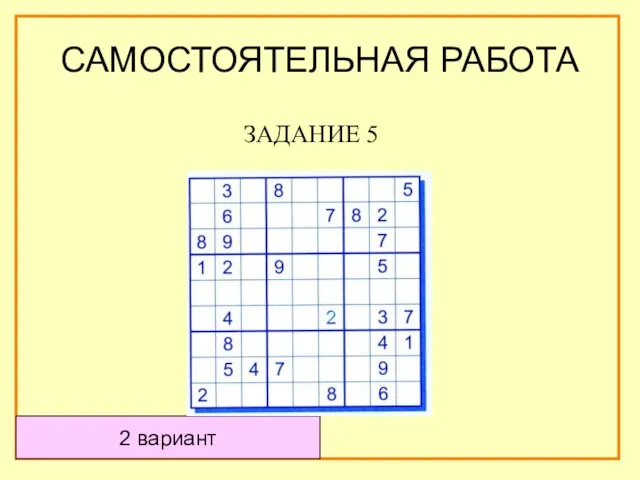
ЗАДАНИЕ 5
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

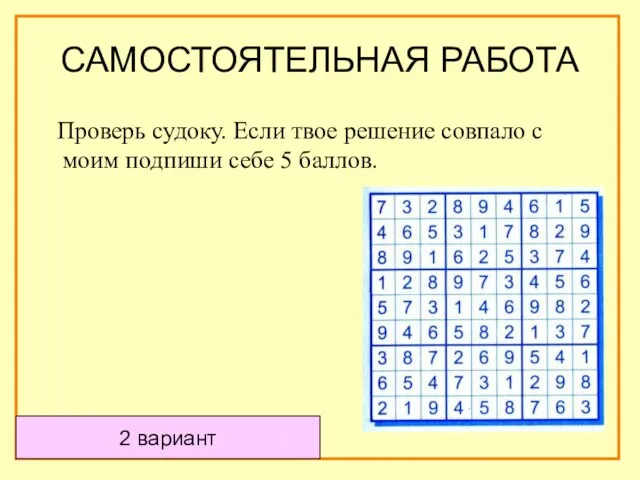
Проверь судоку. Если твое решение совпало с моим подпиши себе 5 баллов.
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

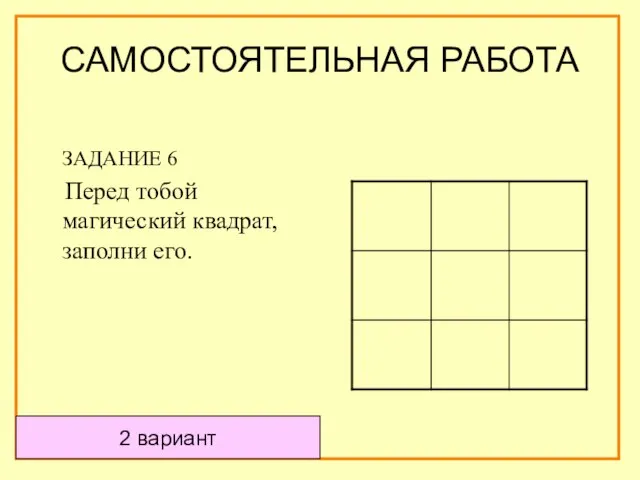
ЗАДАНИЕ 6
Перед тобой магический квадрат, заполни его.
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

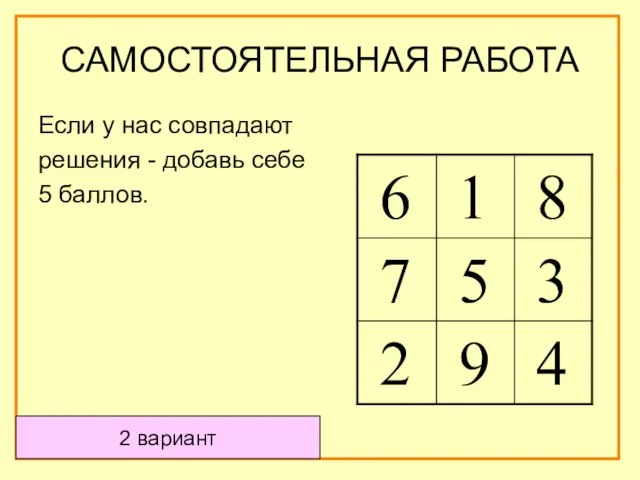
2 вариант
Если у нас совпадают
решения - добавь себе
5 баллов.
САМОСТОЯТЕЛЬНАЯ РАБОТА

Подведём итоги. Если ты набрал
от 30 до 25 баллов - ты заработал 5;
от 20 до 10 баллов – твоя оценка 4;
5 баллов – у тебя 3,
но, а если ты не набрал ни одного балла не отчаивайся и попробуй решить задания еще раз. Я уверена, что у тебя все получится.
2 вариант
САМОСТОЯТЕЛЬНАЯ РАБОТА

КОНТРОЛЬНАЯ РАБОТА
1 вариант
2 вариант

КОНТРОЛЬНАЯ РАБОТА
ЗАДАНИЕ 1
Угорь плыл по реке со скоростью 12 километров в час. Какова скорость течения, если всего угорь проплыл 85 километров за 5 часов?
1 вариант

Проверяй-ка!
12 х 5 = 60 (километров проплыл угорь)
85 – 60 = 25 (километров за 5 часов)
25 : 5 = 5 (километров в час скорость течения)
1 вариант
КОНТРОЛЬНАЯ РАБОТА

ЗАДАНИЕ 2
Две кожистые черепахи должны были съесть 350 крупных медуз. Первая черепаха может съесть их за неделю. Через 3 дня были съедены все медузы. Сколько медуз съела вторая черепаха?
1 вариант
КОНТРОЛЬНАЯ РАБОТА

Не забывай проверять решение.
7 : 350 = 1/5 (часть медуз съедает первая черепаха)
1/5 х 3 = 3/5 (части медуз съедает за 3 часа первая черепаха)
1 – 3/5 = 2/5 (части медуз съела вторая черепаха)
350 х 2/5 = 140 (медуз съела вторая черепаха)
КОНТРОЛЬНАЯ РАБОТА

ЗАДАНИЕ 3
Цапля-мама съела 2/3 части всех лягушек, находившихся в болоте. Сын цапли съел 1/6 часть болотных лягушек, а дочь цапли-мамы съела 12 оставшихся квакушек. Сколько лягушек жили в болоте?
1 вариант
КОНТРОЛЬНАЯ РАБОТА

Проверка:
2/3 + 1/6 = 5/6 (части лягушек съела мама и сын)
1 – 5/6 = 1/6 (часть всех лягушек съела дочь цапли)
12 : 1/6 = 72 (лягушки жили в болоте)
КОНТРОЛЬНАЯ РАБОТА
1 вариант

ЗАДАНИЕ 4
Постарайся заполнить этот магический квадрат.
1 вариант
КОНТРОЛЬНАЯ РАБОТА

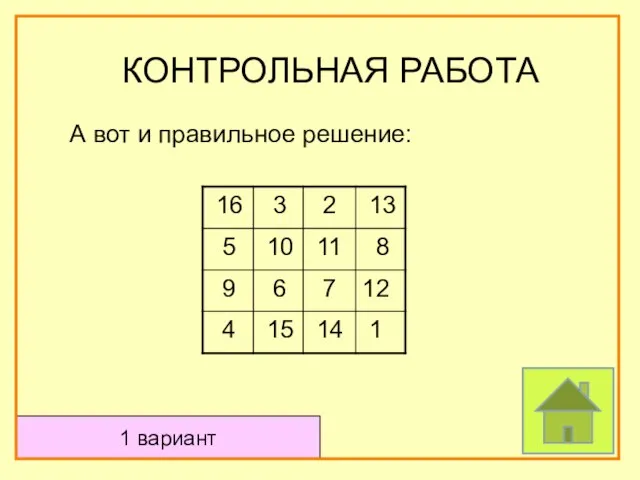
А вот и правильное решение:
КОНТРОЛЬНАЯ РАБОТА
1 вариант

ЗАДАНИЕ 1
Скорость комнатной мухи 3 метра в секунду. Она полетела на шкаф, расстояние до которого равно 22 метрам. К несчастью, встречный ветер мешал полету. Скорость ветра – 1 метр в секунду. Сколько времени понадобилось мухе для достижения цели?
2 вариант
КОНТРОЛЬНАЯ РАБОТА

А вот и мое решение:
3 – 1 = 2 (метра в секунду скорость мухи против течения)
22 : 2 = 11 (секунд понадобилось мухе)
2 вариант
КОНТРОЛЬНАЯ РАБОТА

ЗАДАНИЕ 2
Летучая мышь за один час ловит 60 малярийных комаров. Её подруга ловит за 3 часа 165 малярийных комаров. За сколько времени обе летучие мыши поймают 345 малярийных комаров?
2 вариант
КОНТРОЛЬНАЯ РАБОТА

Проверяй решение!
165 : 3 = 55 (малярийных комаров ловит за час вторая мышь)
55 + 60 = 115 (малярийных комаров ловят за час две летучие мыши)
345 : 115 = 3 (часа нужно летучим мышам)
2 вариант
КОНТРОЛЬНАЯ РАБОТА

Три ежика вместе нашли 56 грибов. Из них 1/7 часть нашел ежик Гриша, 1/6 часть оставшихся грибов нашла ежиха Глаша, 20 оставшихся грибов они отдали маме-ежихе. Сколько грибов нашел еж Гоша?
КОНТРОЛЬНАЯ РАБОТА
2 вариант

А вот и проверка:
56 х 1/7 = 8 (грибов нашел Гриша)
56 – 8 = 48 (грибов осталось)
48 х 1/6 = 8 (грибов нашла Глаша)
48 – 8 = 40 (грибов осталось)
40 – 20 = 20 (грибов нашел Гоша)
2 вариант
КОНТРОЛЬНАЯ РАБОТА

ЗАДАНИЕ 4
Постарайся правильно заполнить этот магический квадрат:
КОНТРОЛЬНАЯ РАБОТА
2 вариант

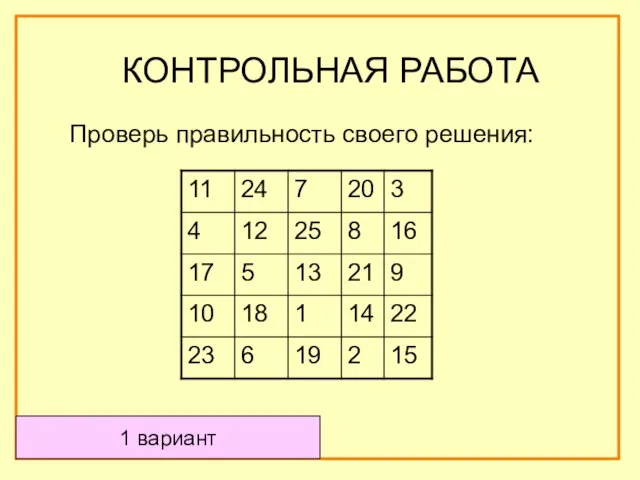
Проверь правильность своего решения:
КОНТРОЛЬНАЯ РАБОТА
1 вариант

Если ты набрал…
20 баллов – 5.
15 баллов у тебя 4.
10 баллов к сожалению у тебя 3.
5 баллов – потрудись хорошенько и попробуй снова.
0 баллов – тебе надо упорно заниматься математикой.
КОНТРОЛЬНАЯ РАБОТА

Терминологический словарик
1. Производительность – часть работы, выполняемая кем-либо за 1 день
2. t х v = S; S : t = v, S : v = t где
S – расстояние
t – время
v – скорость
3. Время сближения – это время через которое произойдет сближение.
4. Время удаления – это время, по прошествии которого объекты находятся друг от друга на определённом расстоянии.

Движение вдогонку – это вид движения, во время которого один объект (чаще всего с большей скоростью) догоняет другой.
6. (v теч. + v объекта) х t = S, где
v - скорость
t – время
S - расстояние
7. (v объекта - v теч.) х t = S, где
v - скорость
t – время
S - расстояние
Терминологический словарик