Содержание
- 2. План доклада Что такое и для чего нужна томография квантовых состояний? Варианты решения проблемы реконструкции. Вероятностное
- 3. Как описать состояние спина? Спин j, собственные векторы операторов и Чистые состояния: Смешанные состояния Секция «Теоретическая
- 4. Как восстановить оператор плотности, используя результаты наблюдений? Наблюдаемая А, среднее значение - измеримо Пример: проекторы Матрица
- 5. Томография состояния спина Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля 2010 г.
- 6. Опыт Штерна-Герлаха (1922) Вероятность Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля 2010 г.
- 7. Предельный случай бесконечного числа направлений n – интегрирование по сфере V. V. Dodonov and V. I.
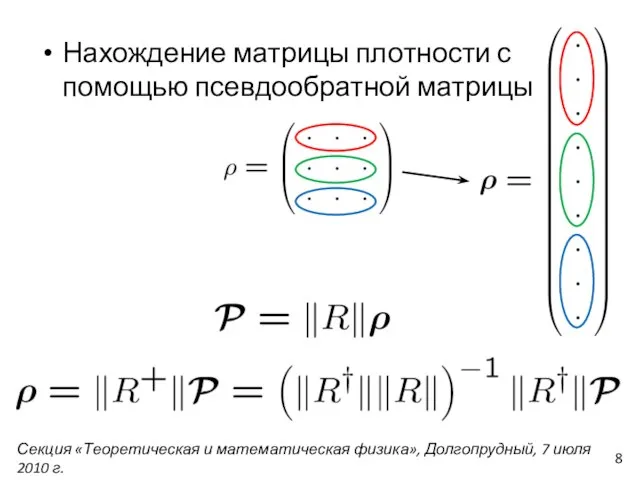
- 8. Нахождение матрицы плотности с помощью псевдообратной матрицы Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля 2010
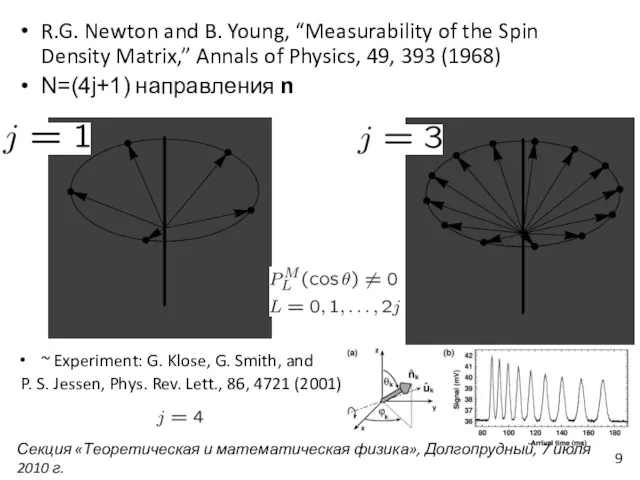
- 9. R.G. Newton and B. Young, “Measurability of the Spin Density Matrix,” Annals of Physics, 49, 393
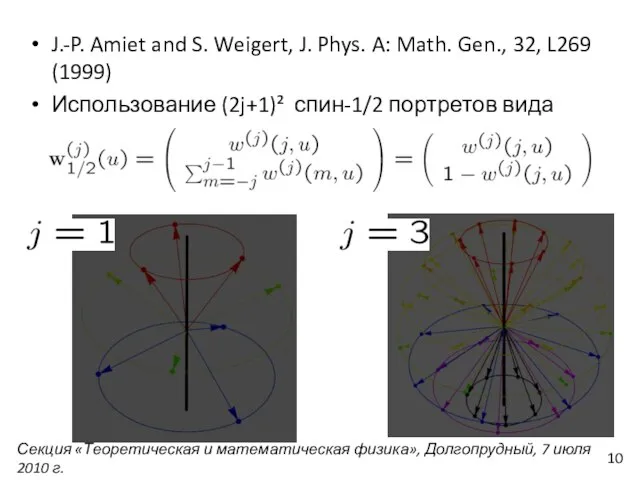
- 10. J.-P. Amiet and S. Weigert, J. Phys. A: Math. Gen., 32, L269 (1999) Использование (2j+1)² спин-1/2
- 11. Спиновая томограмма с конечным числом «вращений» Спин j, число направлений = 4j+1 Вероятностное представление Реконструкция «Квантайзер»
- 12. Математический аппарат Задача на операторы матрица Грама ? Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля
- 13. Кубит (спин 1/2) Вероятностное представление Реконструкция Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля 2010 г.
- 14. Уравнение эволюции томограмм Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля 2010 г.
- 15. Диаграмма направленности распада мюона и томограмма кубитов Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля 2010
- 16. Диаграмма направленности распада мюона и томограмма кубитов Секция «Теоретическая и математическая физика», Долгопрудный, 7 июля 2010
- 17. Выводы Рассмотрены варианты решения задачи реконструкции квантового состояния и предложен новый метод, основанный на конечном числе
- 19. Скачать презентацию













 Сопротивление человека
Сопротивление человека Формы проявления психических процессов и их взаимосвязь
Формы проявления психических процессов и их взаимосвязь Студенческий Event. Понятие бренда
Студенческий Event. Понятие бренда Презентация на тему Влияние на жизнь и здоровье людей природных катастроф
Презентация на тему Влияние на жизнь и здоровье людей природных катастроф Adidas performance outdoor ss'22
Adidas performance outdoor ss'22 Incubation. Illumination
Incubation. Illumination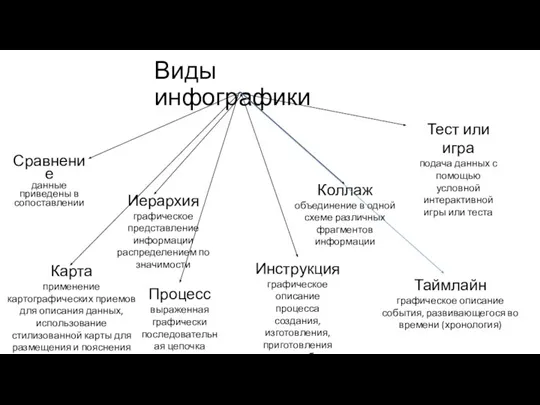 Инфографика
Инфографика Теория государства и права. Происхождение государства
Теория государства и права. Происхождение государства ФасадДомСтрой
ФасадДомСтрой Правовое регулирование реализации товаров, работ, услуг. Тема 6
Правовое регулирование реализации товаров, работ, услуг. Тема 6 Живая память
Живая память Критическое состояние окружающей природной среды в России
Критическое состояние окружающей природной среды в России Долина гейзеров на полуострове Камчатка
Долина гейзеров на полуострове Камчатка United Kingdom Political System
United Kingdom Political System Высшее образования 2010 год. Проблемы, задачи, перспективы развития
Высшее образования 2010 год. Проблемы, задачи, перспективы развития Наследственное право РФ
Наследственное право РФ Презентация на тему Древний Восток и античный мир 10 класс
Презентация на тему Древний Восток и античный мир 10 класс Источники и институты классического средневекового права
Источники и институты классического средневекового права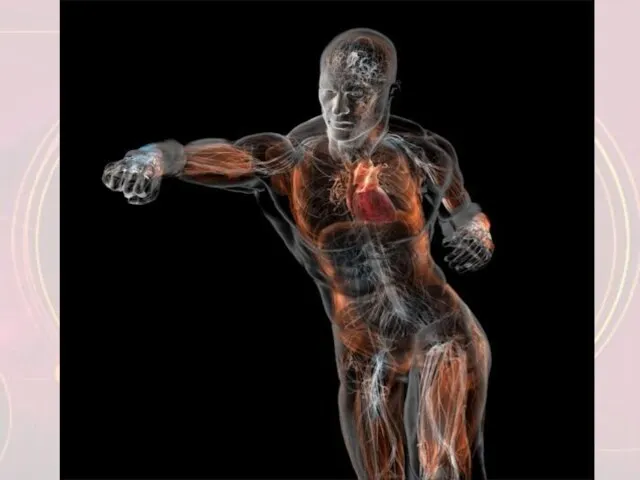 Изучение органов кровообращения человека
Изучение органов кровообращения человека Задачи по теме
Задачи по теме Вагинальные инфекции
Вагинальные инфекции бенчмарки_карточка_товара_акции
бенчмарки_карточка_товара_акции 1
1 불규칙 동사
불규칙 동사 Transformatori
Transformatori Ama Kids, рейтинг
Ama Kids, рейтинг Вирусы гриппа
Вирусы гриппа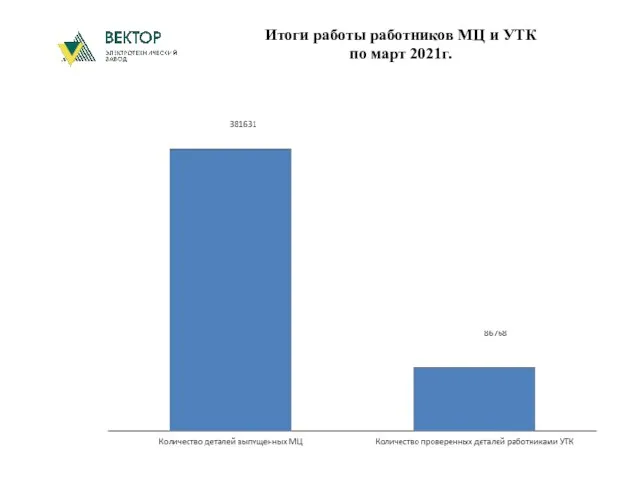 Электротехнический завод Вектор. Итоги работы работников МЦ и УТК
Электротехнический завод Вектор. Итоги работы работников МЦ и УТК