Содержание
- 2. Французский ученый Луи де Бройль (1892—1987), выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма: не
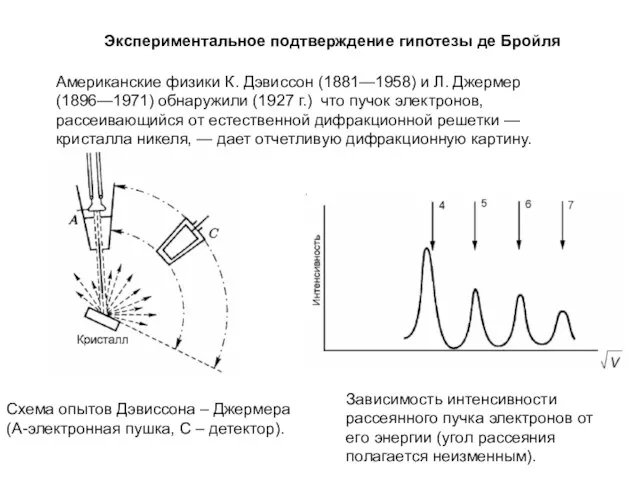
- 3. Экспериментальное подтверждение гипотезы де Бройля Американские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили (1927
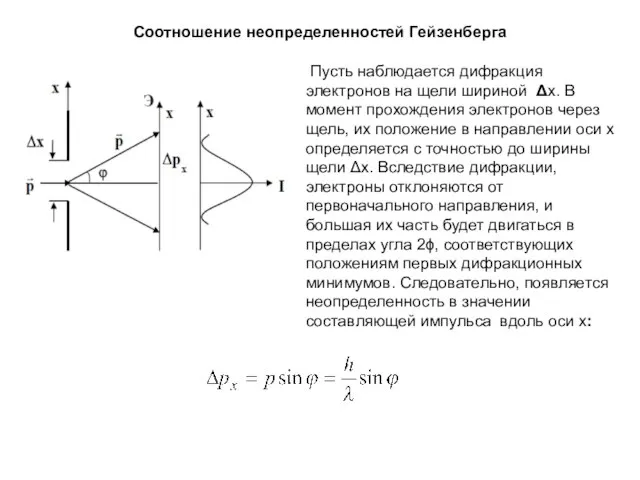
- 4. Соотношение неопределенностей Гейзенберга Пусть наблюдается дифракция электронов на щели шириной Δx. В момент прохождения электронов через
- 5. Первый дифракционный минимум определяется из условия: λ – длина волны де Бройля. Исключая sinϕ , получим:
- 6. В квантовой теории рассматривается также соотношение неопределенностей для энергии E и времени t. Неопределенности этих величии
- 7. Волновая функция и ее свойства Интенсивность волн де Бройля в данной точке пространства связана с числом
- 8. Величина имеет смысл плотности вероятности ρw Сама волновая функция Ψ имеет смысл амплитуды вероятности. Условие нормировки
- 9. Волновая функция позволяет вычислить средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние имеет вид:
- 10. Общее уравнение Шредингера Основное уравнение нерелятивистской квантовой механики имеет вид m - масса частицы; - оператор
- 11. Уравнение Шредингера для стационарных состояний Важным частным случаем общего уравнения Шредингера, является уравнение Шредингера для стационарных
- 12. После упрощений получим уравнение Шредингера для стационарных состояний: или Физический смысл имеют только регулярные волновые функции
- 13. Движение свободной частицы Пусть свободная частица движется вдоль оси x. Для такой частицы U(x)=0. Уравнение Шредингера
- 14. Частица в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками" Рассмотрим частицу в одномерной "потенциальной яме"
- 15. Этим граничным условиям удовлетворяет решение уравнения Шредингера при и Поскольку то Таким образом, энергия частицы в
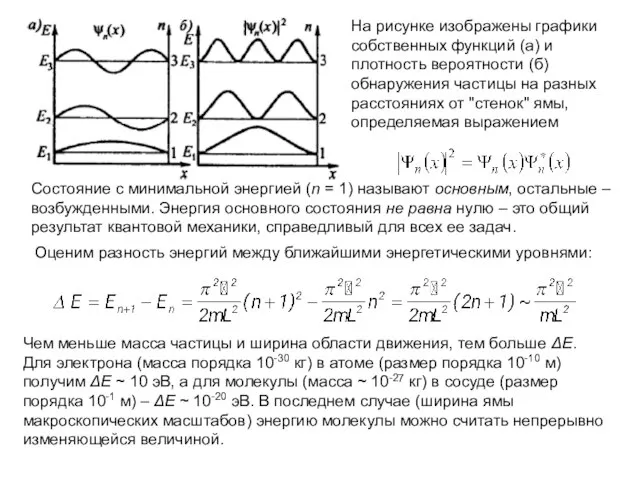
- 16. На рисунке изображены графики собственных функций (а) и плотность вероятности (б) обнаружения частицы на разных расстояниях
- 18. Скачать презентацию












 совместно с Театром праздника «Солнечный зайчик»
совместно с Театром праздника «Солнечный зайчик» ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс
ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс Презентация на тему Врожденные и приобретенные программы поведения
Презентация на тему Врожденные и приобретенные программы поведения Презентация
Презентация ПРОЕКТНАЯ РАБОТА
ПРОЕКТНАЯ РАБОТА к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич
к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич Культура Руси в 10 – 13 веках
Культура Руси в 10 – 13 веках Болгария в 20-30-е годы
Болгария в 20-30-е годы Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя
Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя Приготовление завтрака
Приготовление завтрака «Инвестиционная политика муниципального образования на современном этапе»02.02.2012
«Инвестиционная политика муниципального образования на современном этапе»02.02.2012 Работа академии по направлению научно-технического творчества молодежи
Работа академии по направлению научно-технического творчества молодежи «Трудные» дети и их проблемы.
«Трудные» дети и их проблемы. Приемы расположения к себе. Самопрезентация
Приемы расположения к себе. Самопрезентация Автохимия. Завод автохимии
Автохимия. Завод автохимии Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года
Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года Евангелие от Матфея
Евангелие от Матфея Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов
Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов Аварийная аптечка для первой медицинской помощи
Аварийная аптечка для первой медицинской помощи Власть. Сила. Лекция 2
Власть. Сила. Лекция 2 Вітражі та шпроси
Вітражі та шпроси Моя будущая профессия - бухгалтер
Моя будущая профессия - бухгалтер Олимпиада үрләренә - баскычлап
Олимпиада үрләренә - баскычлап Общероссийские антидопинговые правила
Общероссийские антидопинговые правила Проектирование транспортно-грузовых комплексов
Проектирование транспортно-грузовых комплексов Определение размеров молекул октана
Определение размеров молекул октана Такси Лось
Такси Лось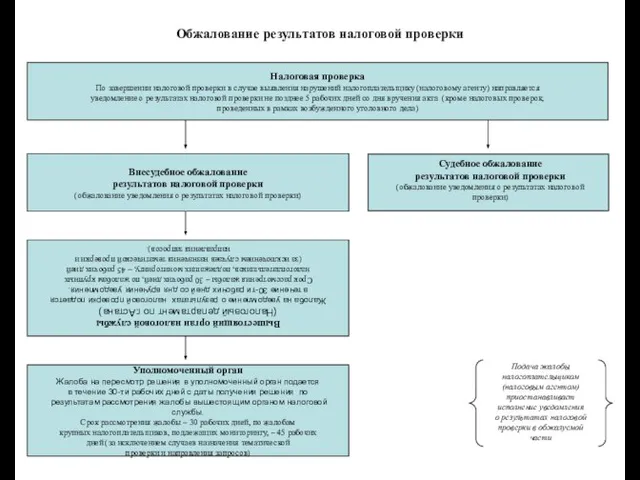 Обжалование результатов налоговой проверки
Обжалование результатов налоговой проверки