Вписанная и описанная окружность

Цели и задачи урока
Учить применять свойства вписанной и описанной окружности при решении задач;
Развивать самостоятельность, логически мыслить и правильно выражать свои мысли;

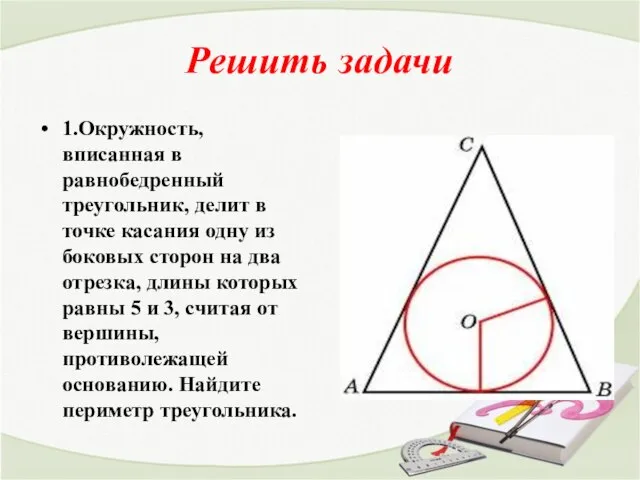
Решить задачи
1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

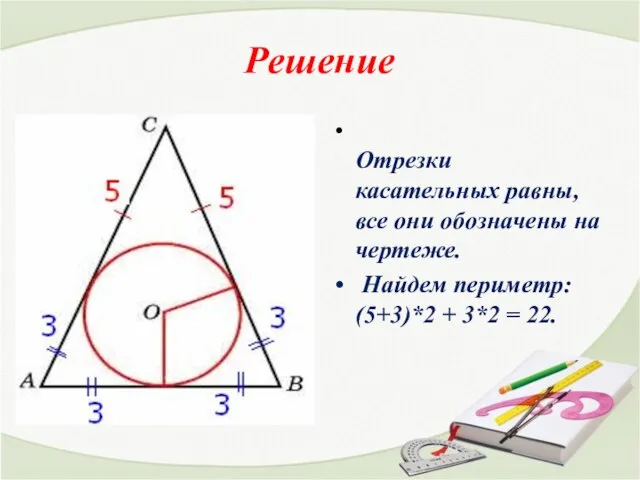
Решение
Отрезки касательных равны, все они обозначены на чертеже.
Найдем периметр: (5+3)*2 + 3*2 = 22.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

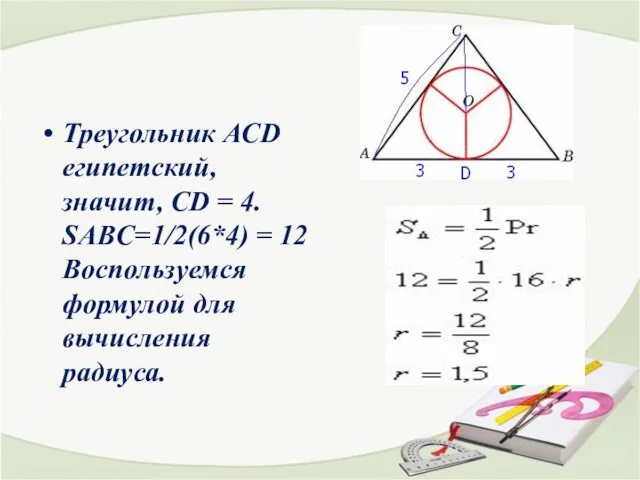
Треугольник АСD египетский, значит, СD = 4. SABC=1/2(6*4) = 12 Воспользуемся формулой для вычисления радиуса.

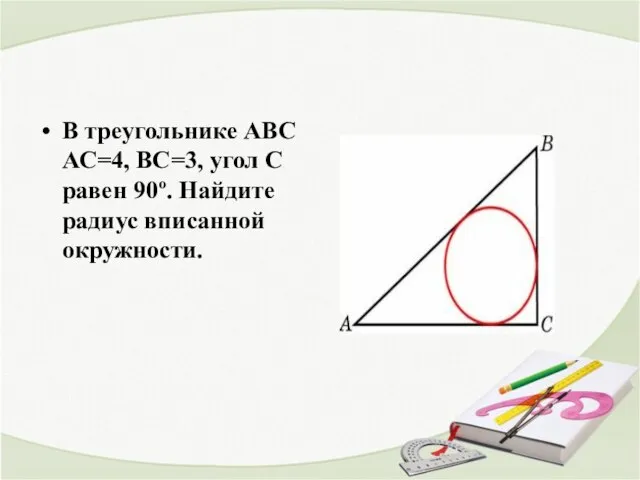
В треугольнике ABC АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.

Решение
АВ=5 (это египетский треугольник).
Р- полупериметр
Р=6

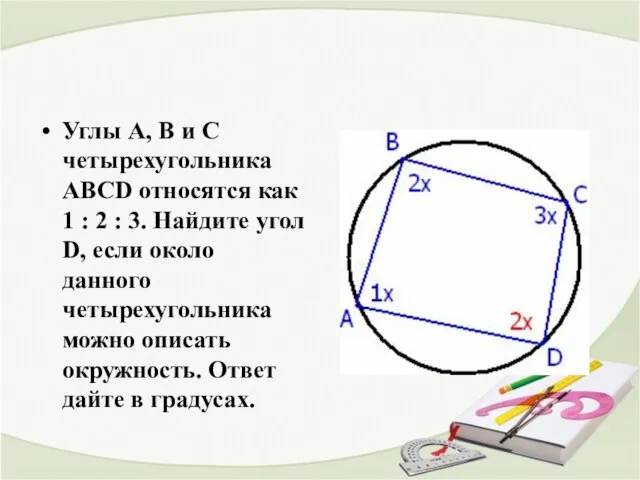
Углы А, В и С четырехугольника ABCD относятся как 1 : 2 : 3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.

Решение
Пусть углы 1х, 2х, 3х. По условию около данного четырехугольника можно описать окружность
А+С = D+B.
Тогда угол D=2х.
Сумма противоположных углов описанного четырехугольника 180.
1х+3х=180 (или 2х+2х=180)
х=45 (1 часть)
Угол D=90

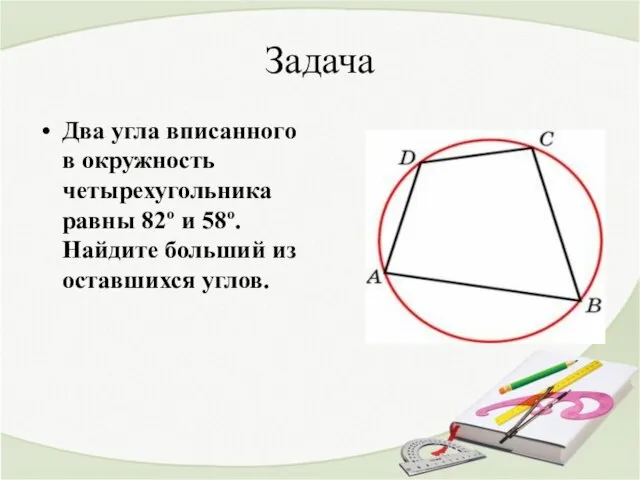
Задача
Два угла вписанного в окружность четырехугольника равны 82º и 58º. Найдите больший из оставшихся углов.

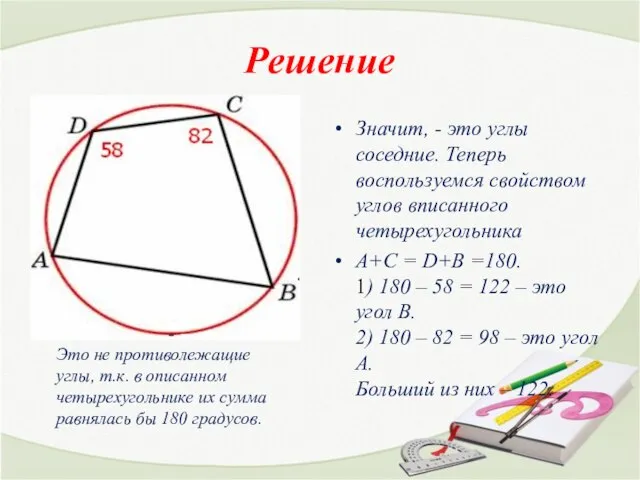
Решение
Значит, - это углы соседние. Теперь воспользуемся свойством углов вписанного четырехугольника
А+С = D+B =180.
1) 180 – 58 = 122 – это угол В.
2) 180 – 82 = 98 – это угол А.
Больший из них – 122.
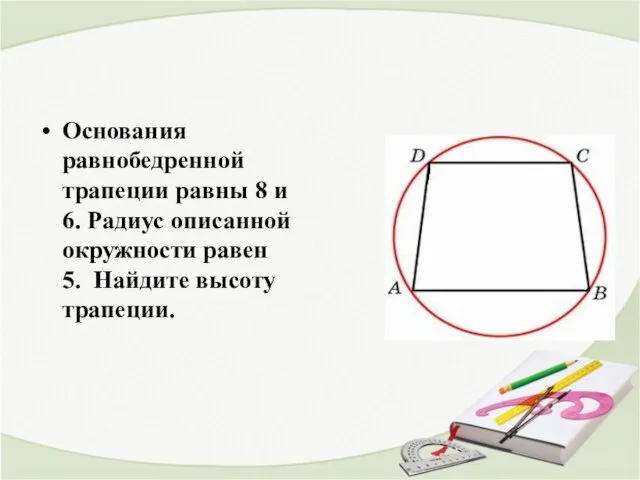
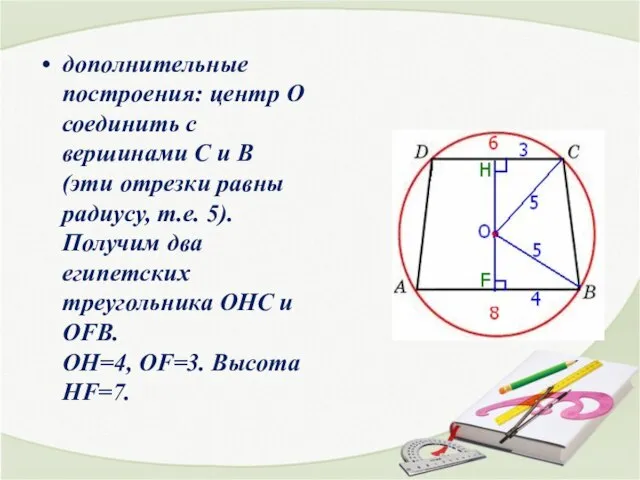
Это не противолежащие углы, т.к. в описанном четырехугольнике их сумма равнялась бы 180 градусов.

Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

дополнительные построения: центр О соединить с вершинами С и В (эти отрезки равны радиусу, т.е. 5). Получим два египетских треугольника ОHC и OFB.
ОH=4, OF=3. Высота HF=7.

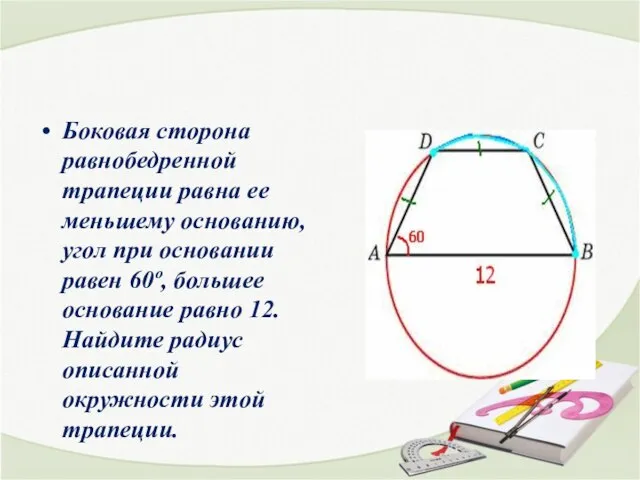
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60º, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Решение
Вписанный угол ВАD опирается на дугу DCB.
дуга DCB=120, а дуга DC = 60.
Три дуги стягивают равные хорды AD, DC, CB. Они равны 60. Тогда дуга AB= 180. а это означает, что АВ – диаметр, тогда радиус 12:2 = 6.

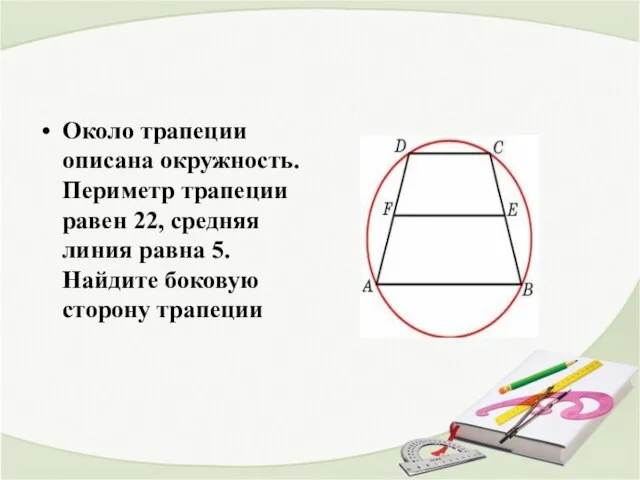
Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции

Решение
1) Средняя линия равна полусумме оснований. Тогда сумма оснований равна 10.
2) 22 – 10 = 12 это приходиться на боковые стороны.
3) 12:2 = 6, боковые стороны вписанной трапеции равны.

Интернет-ресурсы
Книга:
http://www.liveinternet.ru/users/4321745/post201324261/
Карандаш: http://allforchildren.ru/pictures/showimg/school5/school0519jpg.htm
Линейка, циркуль, лекало:
http://www.ineedsex.ru/main.php?g2_view=core.DownloadItem&g2_itemId=345&g2_serialNumber=2
Транспортир: http://knopka48.ru/images/detailed/1/26449_2.png