Временная динамика ультрарелятивистского ускорения слаборелятивистских заряженных частиц в космической плазме при серфинге на
- Главная
- Разное
- Временная динамика ультрарелятивистского ускорения слаборелятивистских заряженных частиц в космической плазме при серфинге на

Содержание
- 2. Аннотация. Серфинг заряженных частиц на электромагнитных волнах является одним из главных механизмов генерации потоков ультрарелятивистских частиц
- 3. Характерные времена захвата частиц в режим серфинга относительно невелики по сравнению с оптимальным вариантом реализации серфинга
- 4. Введение Исследование процессов генерации потоков релятивистских частиц относится к числу актуальных задач физики космической плазмы и,
- 5. Отметим, что серфинг возможен и при наклонном распространении волн причем пороговая величина поля волны меньше. Рассмотрен
- 6. Формулировка задачи Исходными являются релятивистские уравнения движения заряженной частицы, взаимодействующей с электромагнитной волной, фазовая скорость которой
- 7. Введем безразмерное время τ = ω t. Характерное время пересечения захваченным зарядом волнового пакета порядка δt
- 8. Численные расчеты показали, что в области волнового пакета, где амплитуда электрического выше порогового значения, а скорость
- 9. Захват заряда в режим серфинга сильно зависит от значения начальной фазы Ψ(0) причем весьма немонотонно. Для
- 10. Рис.1. График фазы пакета на несущей частоте для части-цы, с захватом при τ ~ 17223. До
- 11. Рис.3а. Отметим малые вариации скорости при циклотронном враще-нии за счет нелинейно-сти и нестационарности эффективного потен-циала. Частица
- 12. Рис.3б. Отметим малые вариации скорости при циклотронном вращении, обусловленные нелинейностью и нестационарностью эффективного потенциала. На указанном
- 13. Рис.4а. После захвата заряда темп набора им энергии от волнового пакета практи-чески постоя-нен. Пусть Φ(τ) =
- 14. Рис.4б. Динамика релятивистского фактора частицы на малых временах, когда она еще не захвачена волновым пакетом и
- 15. Рис.5. Структура фазовой плоскости частицы на временном интервале τ
- 16. Обратим внимание на то, что в режиме ускорения частицы изображающая точка на фазовой плоскости на плоскости
- 17. Расчеты для других вариантов параметров слаборелятивистской частицы при ее захвате волной в космической плазме с последующим
- 18. Следовательно, кроме выполнения условия черенковского резонанса волна-частица оптимальным для сильного ускорения электронов является, в соответствии с
- 19. Во время ускорения компоненты импульса и релятивистский фактор частицы возрастают с постоянным темпом. Для оптимальной реализации
- 20. Заметим, что серфинг зарядов возможен и при наклонном (к внешнему магнит-ному полю) распространении электромагнитных волн, приме
- 21. 8. Ерохин Н.С., Зольникова Н.Н., Хачатрян А.Г. Ускорение зарядов поперек маг-нитного поля при взаимодействии сильной плазменной
- 23. Скачать презентацию
Слайд 2Аннотация.
Серфинг заряженных частиц на электромагнитных волнах является одним из главных механизмов
Аннотация.
Серфинг заряженных частиц на электромагнитных волнах является одним из главных механизмов

Слайд 3Характерные времена захвата частиц в режим серфинга относительно невелики по сравнению с
Характерные времена захвата частиц в режим серфинга относительно невелики по сравнению с

Рассмотрена временная динамика компонент импульса и скорости ускоряемых частиц, характерные особенности их траектории с учетом гировращения на начальном этапе, типичная структура фазовой плоскости для исследуемого нелинейного уравнения.
Слайд 4Введение
Исследование процессов генерации потоков релятивистских частиц относится к числу актуальных задач
Введение
Исследование процессов генерации потоков релятивистских частиц относится к числу актуальных задач

В работе на основе нелинейных численных расчетов рассмотрен захват слаборелятивистских заряженных частиц в режим серфотронного ускорения пакетом электромагнитных волн, распространяющимся в плазме поперек слабого внешнего магнитного поля H0 .
Слайд 5Отметим, что серфинг возможен и при наклонном распространении волн причем пороговая величина
Отметим, что серфинг возможен и при наклонном распространении волн причем пороговая величина

Рассмотрен вариант ускорения слаборелятивистских частиц, когда период циклотронного вращения заряда сравнительно невелик. Для амплитуды волны выше порогового значения на доступных интервалах времени численного счета вне диапазона благоприятных для серфинга начальных фаз волны на траектории частицы вначале происходит вращение заряда во внешнем магнитном поле Однако после ряда периодов циклотронного вращения (десятки, сотни и более) будет выполнено условие черенковского резонанса, возникает благоприятная для захвата заряда фаза волны на траектории частицы.
При этом происходят захват частицы волновым пакетом и ультрарелятивистское ускорение заряда. Следовательно, в пространстве импульсов частиц область их захвата в режим серфинга на электромагнитной волне оказывается достаточно большой.
Полученные результаты представляют интерес для интерпретации эксперимен-тальных данных по регистрации потоков релятивистских частиц в космических условиях. Серфинг зарядов на электромагнитных волнах может быть локальным источником генерации ультрарелятивистских частиц в окрестности сравнительно спокойных звезд, например, в солнечной гелиосфере, и обеспечивать локальные отклонения регистрируемого спектра КЛ от стандартного степенного скейлинга.
Слайд 6Формулировка задачи
Исходными являются релятивистские уравнения движения заряженной частицы, взаимодействующей с
Формулировка задачи
Исходными являются релятивистские уравнения движения заряженной частицы, взаимодействующей с

Отметим, что механизм серфотронного ускорения связан с реализацией в магнитоактивной плазме черенковского резонанса при взаимодействии волна-частица, что возможно для волны р-поляризации с показателем преломления
N2 = ε⊥ - (εc2 / ε⊥ ) = 1 – [ v (1 – v )] / (1 – u2 – v). Внешнее магнитное поле направлено вдоль оси z : H0 = H0 ez . Захват в режим серфинга происходит для амплитуд волны выше порога т.е. σ = e E / m c ω > σc ≡ u γp = u / ( 1 - βp2 ) 1 / 2, где βp = ω / k c . Рассмотрим волновой спектр с несущей частотой ω0 = ω(k0). Имеем параметры: u = ωHe /ω, v = (ωpe /ω)2. Здесь ωHe - гирочастота нерелятивистских электронов плазмы, ωpe – их ленгмюровская частота ωpe = ( 4 π e2 n0 / m )1/2 . При поперечном распространении волна р-поляризации имеет компоненты полей Ex , Ey , Hz . Для лоренцовского спектра волн в пакете основная компонента электрического поля имеет вид Ex(x,t) = { Em / [ 1 + ζ2 / L2 ] } cos (ω0 t – k0 x ),
где ζ = x – vg(k0) t , L = 1 / kp есть полуширина локализованного волнового пакета, движущегося со скоростью vg(k0). Другие компоненты полей пакета Ey , Hz нахо-дятся по аналогии.
Слайд 7Введем безразмерное время τ = ω t. Характерное время пересечения захваченным зарядом
Введем безразмерное время τ = ω t. Характерное время пересечения захваченным зарядом

Оценки и расчеты показывают, что можно пренебречь вихревыми компонентами волновых полей Ey , Hz и для фазы пакета на несущей частоте Ψ0(τ) = (ω0 t – k0 x) использовать нелинейное уравнение
βp0 d2Ψ0 /dτ2 – (1 - βx2) ⋅ (e Ex / mcω0) – u0 βy = 0, (1)
где Ex(x,t) определено выше, βp0 = ω0 /ck0 , γ = (1 + h2 + r02 )0.5/ ( 1 - βx2 )0.5 , r0 = γ βy начальный импульс частицы вдоль волнового фронта и учтен интеграл движения J = γ βy + u0 βp0 (Ψ0 - τ). Есть второй интеграл γ βz = const ≡ h. Компонента скорости заряда βx в (1) задана формулой βx = βp0 [ 1 – ( dΨ0 / dτ ) ].
Уравнение (1) решалось численно, например, для следующих значений исходных параметров : u = 0.3, βp0 = 0.8, h = 0.4, g = 0.7, ρ = 5⋅104 , σ = 1.51 σc .
Слайд 8Численные расчеты показали, что в области волнового пакета, где амплитуда электрического выше
Численные расчеты показали, что в области волнового пакета, где амплитуда электрического выше

Набор энергии частицей возрастает с увеличением характерной толщины вол-нового пакета. Согласно численным расчетам при ускорении захваченной час-тицы ее релятивистский фактор и поперечные к внешнему магнитному полю компоненты импульса возрастают пропорционально времени удержания заряда волновым пакетом в эффективной потенциальной яме.
Поперечные компоненты скорости заряда выходят на асимптотические значе-ния, а продольная (относительно внешнего магнитного поля) скорость стремит-ся к нулю вследствие сохранения продольного импульса. С течением времени ускоряемые частицы конденсируются на дно нестационарной, эффективной потенциальной ямы.
Приведем результаты расчетов для следующего варианта выбора параметров задачи h = 0.61, gy(0) = 0.91, βp = 0.7, u = 0.2, σ = 1.5 σc , σc = u γp , а = 0,
соответствующего слаборелятивистским начальным энергиям заряженной частицы.
Слайд 9Захват заряда в режим серфинга сильно зависит от значения начальной фазы Ψ(0)
Захват заряда в режим серфинга сильно зависит от значения начальной фазы Ψ(0)

Слайд 10Рис.1. График фазы пакета на несущей частоте для части-цы, с захватом при
Рис.1. График фазы пакета на несущей частоте для части-цы, с захватом при
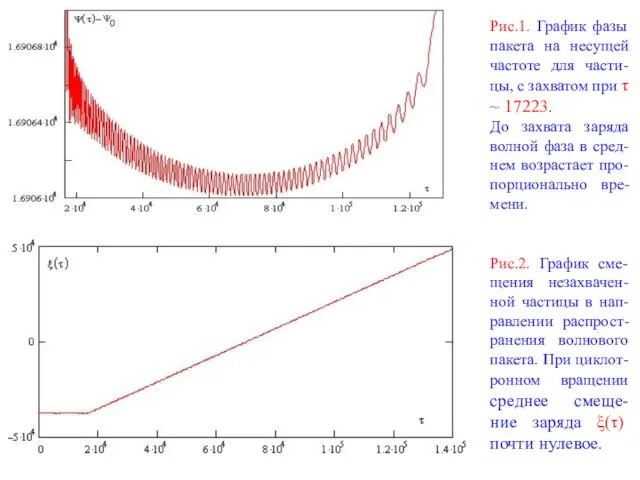
До захвата заряда волной фаза в сред-нем возрастает про-порционально вре-мени.
Рис.2. График сме-щения незахвачен-ной частицы в нап-равлении распрост-ранения волнового пакета. При циклот-ронном вращении среднее смеще-ние заряда ξ(τ) почти нулевое.
Слайд 11Рис.3а. Отметим малые вариации скорости при циклотронном враще-нии за счет нелинейно-сти и
Рис.3а. Отметим малые вариации скорости при циклотронном враще-нии за счет нелинейно-сти и
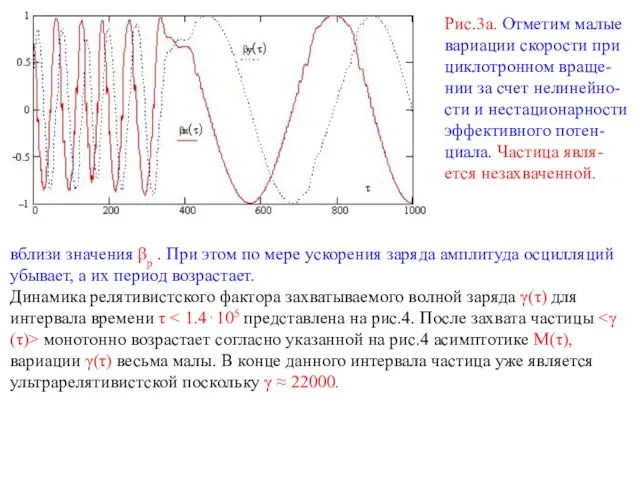
вблизи значения βp . При этом по мере ускорения заряда амплитуда осцилляций убывает, а их период возрастает.
Динамика релятивистского фактора захватываемого волной заряда γ(τ) для интервала времени τ < 1.4⋅105 представлена на рис.4. После захвата частицы <γ(τ)> монотонно возрастает согласно указанной на рис.4 асимптотике M(τ), вариации γ(τ) весьма малы. В конце данного интервала частица уже является ультрарелятивистской поскольку γ ≈ 22000.
Слайд 12Рис.3б. Отметим малые вариации скорости при циклотронном вращении, обусловленные нелинейностью и нестационарностью
Рис.3б. Отметим малые вариации скорости при циклотронном вращении, обусловленные нелинейностью и нестационарностью
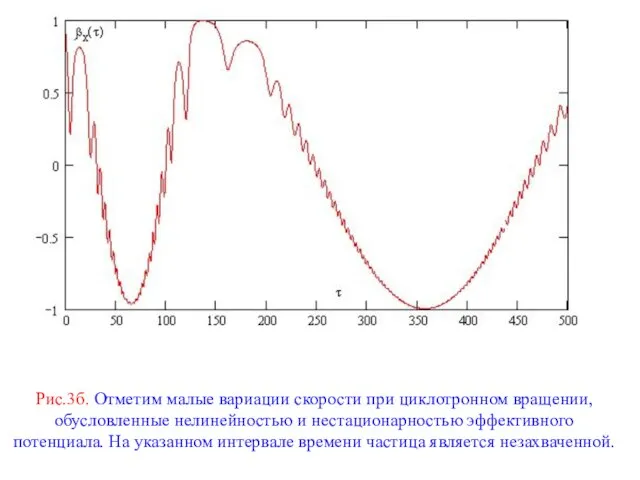
Слайд 13
Рис.4а.
После захвата заряда темп набора им энергии от волнового пакета
Рис.4а.
После захвата заряда темп набора им энергии от волнового пакета
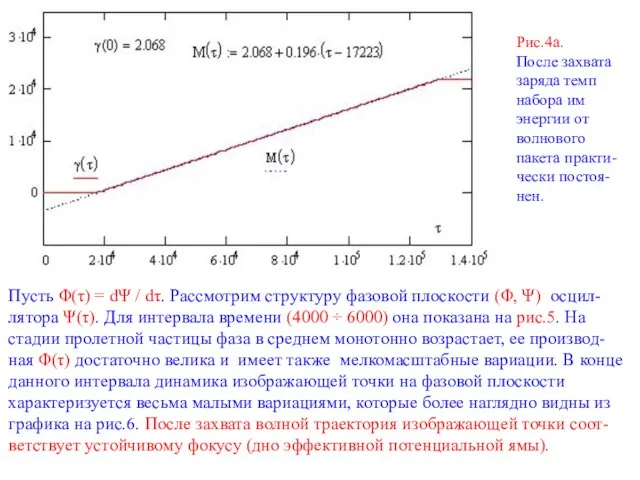
Пусть Φ(τ) = dΨ / dτ. Рассмотрим структуру фазовой плоскости (Φ, Ψ) осцил-лятора Ψ(τ). Для интервала времени (4000 ÷ 6000) она показана на рис.5. На стадии пролетной частицы фаза в среднем монотонно возрастает, ее производ-ная Φ(τ) достаточно велика и имеет также мелкомасштабные вариации. В конце данного интервала динамика изображающей точки на фазовой плоскости характеризуется весьма малыми вариациями, которые более наглядно видны из графика на рис.6. После захвата волной траектория изображающей точки соот-ветствует устойчивому фокусу (дно эффективной потенциальной ямы).
Слайд 14Рис.4б. Динамика релятивистского фактора частицы на малых временах, когда она еще не
Рис.4б. Динамика релятивистского фактора частицы на малых временах, когда она еще не
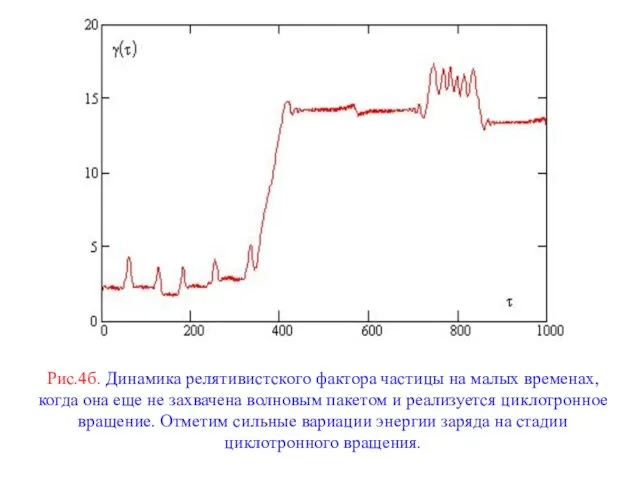
Слайд 15Рис.5. Структура фазовой плоскости частицы на временном интервале τ < 1.4⋅105 .
Рис.5. Структура фазовой плоскости частицы на временном интервале τ < 1.4⋅105 .
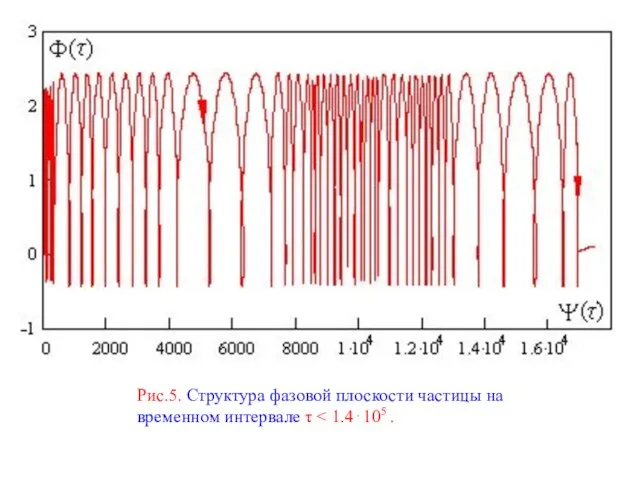
Слайд 16Обратим внимание на то, что в режиме ускорения частицы изображающая точка на
Обратим внимание на то, что в режиме ускорения частицы изображающая точка на
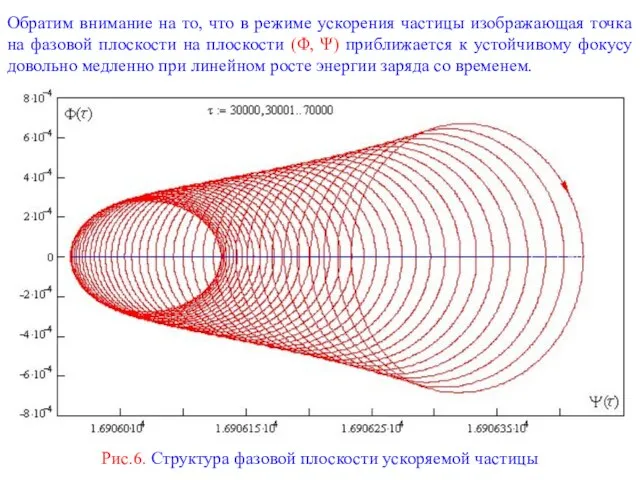
Рис.6. Структура фазовой плоскости ускоряемой частицы
Слайд 17 Расчеты для других вариантов параметров слаборелятивистской частицы при ее захвате волной
Расчеты для других вариантов параметров слаборелятивистской частицы при ее захвате волной

Интересный вариант динамики черенковского взаимодействия электрона с вол-ной возникает при выборе отрицательных начальных значений для компоненты импульса вдоль волнового фронта. Поскольку отрицательное начальное значе-ние компоненты импульса γ βy не соответствует его асимптотике при серфинге заряда на электромагнитной волне, вначале у захваченной частицы происходит перестройка γ βy на положительные значения с уменьшением энергии частицы. При этом темп торможения заряда практически постоянен. Затем после измене-ния знака импульса γ βy имеет место серфотронное ускорение частицы до больших энергий.
Слайд 18Следовательно, кроме выполнения условия черенковского резонанса волна-частица оптимальным для сильного ускорения электронов
Следовательно, кроме выполнения условия черенковского резонанса волна-частица оптимальным для сильного ускорения электронов

Заключение
Результаты настоящей работы состоят в следующем.
1) На основе численных расчетов нелинейного, нестационарного уравнения для фазы пакета на несущей частоте изучено серфотронное ускорение слабореляти-вистских по начальной энергии зарядов в космической плазме волновым пакетом, распространяющимся поперек внешнего магнитного поля. Для слаборелятивист-ской частицы захват в режим серфинга происходит для весьма широкого диапа-зона значений начальной фазы Ψ(0) на траектории частиц и величины расстройки черенковского резонанса. Заряд совершив ряд гирооборотов попадает в благопри-ятную для захвата пакетом фазу при одновременном выполнении черенковского резонанса. Затем происходит ультрарелятивистское ускорение частицы.
Следовательно, число ускоренных волной частиц может быть достаточно большим в результате резкого увеличения в пространстве начальных импульсов области, из которой заряды могут попадать в режим серфотронного ускорения.
Слайд 19Во время ускорения компоненты импульса и релятивистский фактор частицы возрастают с постоянным
Во время ускорения компоненты импульса и релятивистский фактор частицы возрастают с постоянным

2) Зависимость характера ускорения от фазовой скорости волны такова. При вы-боре релятивистских значений фазовой скорости волны наибольшее ускорение идет по направлению распространения волны, темп роста энергии максимален. При низких значениях фазовой скорости основное ускорение происходит вдоль волнового фронта.
Анализ серфинга релятивистских зарядов на электромагнитных волнах пред-ставляет интерес для физики космической плазмы, в частности, для интер-претации экспериментальных данных по регистрации потоков релятивистских частиц в космических условиях. Пакеты электромагнитных волн в окрестностях относительно спокойных звезд типа Солнца могут является локальными источниками генерации космических лучей с энергиями в десятки-сотни Гэв и обеспечивать наблюдаемые отличия спектра КЛ в этом диапазоне от указанной в литературе степенной зависимости.
Слайд 20Заметим, что серфинг зарядов возможен и при наклонном (к внешнему магнит-ному полю)
Заметим, что серфинг зарядов возможен и при наклонном (к внешнему магнит-ному полю)

Литература
1. Katsouleas N., Dawson J.M. Unlimited electron acceleration in laser-driven plasma wave. // Physical Review Letters, 1983, v.51, № 5, pp.392-395.
2. Joshi C. The surfatron laser-plasma accelerators. Prospects and limitations. // Radia-tion in plasmas, 1984, v.1, № 4, pp.514-527.
3. Грибов Б.Э., Сагдеев Р.З., Шапиро В.Д., Шевченко В.И. О затухании плазмен-ных волн и ускорении резонансных электронов в поперечном магнитном поле. // Письма в ЖЭТФ, 1985, т.42, вып.2, с.54-58.
4. Буланов С.В., Сахаров А.С. Ускорение частиц, захваченных сильной потенци-альной волной с искривленным фронтом в магнитном поле. // Письма в ЖЭТФ, 1986, т.44, вып.9, с.421-423.
5. Ситнов М.И. Максимальная энергия частиц в серфатроне в режиме ″неограни-ченного ускорения″. // Письма в ЖТФ, 1988, т.14, вып.1, с.89-92.
6. Ерохин Н.С., Лазарев А.А., Моисеев С.С., Сагдеев Р.З. Увлечение и ускорение заряженных частиц замедленной волной в неоднородной плазме. // ДАН СССР, 1987, т.295, № 4, с.849-852.
7. Ерохин Н.С., Моисеев С.С., Сагдеев Р.З. Релятивистский серфинг в неодно-родной плазме и генерация космических лучей. - Письма в Астрономический журнал, 1989, т.15, № 1, с.3-10.
Слайд 218. Ерохин Н.С., Зольникова Н.Н., Хачатрян А.Г. Ускорение зарядов поперек маг-нитного поля
8. Ерохин Н.С., Зольникова Н.Н., Хачатрян А.Г. Ускорение зарядов поперек маг-нитного поля

9. Кичигин Г.Н. Особенности ускорения электронов в серфотроне. – ЖЭТФ, 1995, т.108, вып.10, с.1342-1354.
10. Кичигин Г.Н. Серфотронный механизм ускорения космических лучей в га-лактической плазме. – ЖЭТФ, 2001, т.119, вып.6, с.1038-1049.
11. В.М.Лозников, Н.С.Ерохин. Переменный источник избытка космических электронов в гелиосфере. Вопросы атомной науки и техники, сер.Плазменная электроника, № 4 (68), с.121-124, 2010.
12. Н.С.Ерохин, Н.Н.Зольникова, Е.А.Кузнецов, Л.А.Михайловская. Динамика релятивистского ускорения заряженных частиц в космической плазме при сер-финге на пакете электромагнитных волн. Вопросы атомной науки и техники, сер. Плазменная электроника, № 4 (68), с.116-120, 2010.
13. Н.С.Ерохин, Н.Н.Зольникова, Л.А.Михайловская. Особенности захвата и серфотронного ускорения ультрарелятивистских частиц в космической плазме в присутствии попутной волны. Вопросы атомной науки и техники, 2008, № 4, с.114-118.
14. A. A. Chernikov, G. Schmidt, A. I. Neishtadt. Unlimited Particle Acceleration by Waves in a Magnetic Field. Physical Review Letters, 1992, v. 68, № 10, pp. 1507-1510.
 Развитие науки Вторая половина XIX века
Развитие науки Вторая половина XIX века Финансовая грамотность дошкольников
Финансовая грамотность дошкольников Встречают по одежке. Дизайн современной одежды
Встречают по одежке. Дизайн современной одежды Проекты использования генераторного газа в коммунальной теплоэнергетике
Проекты использования генераторного газа в коммунальной теплоэнергетике Профессия бухгалтер
Профессия бухгалтер День 4. Применять возрождение на практике
День 4. Применять возрождение на практике История сварочного дела. Славянов Николай Гаврилович
История сварочного дела. Славянов Николай Гаврилович КВАДРАНТ КИЙОСАКИ
КВАДРАНТ КИЙОСАКИ Быстрые методы гигиенического мониторинга
Быстрые методы гигиенического мониторинга Каменная соль – чудо-минерал
Каменная соль – чудо-минерал "Воспитание толерантности"
"Воспитание толерантности" АВТОМАТИЗАЦИЯ ЗВУКА Р, Рь В СЛОВАХ
АВТОМАТИЗАЦИЯ ЗВУКА Р, Рь В СЛОВАХ ЦЕЛЬ: РАСШИРИТЬ ЗНАНИЕ УЧАЩИХСЯ О ПРАВИЛЬНОМ ПИТАНИИ
ЦЕЛЬ: РАСШИРИТЬ ЗНАНИЕ УЧАЩИХСЯ О ПРАВИЛЬНОМ ПИТАНИИ Подготовка к ВПР (№ 8) (геометрические задания). Математика. УМК: любой. 6 класс
Подготовка к ВПР (№ 8) (геометрические задания). Математика. УМК: любой. 6 класс Жизнь и творчество Д.Н.Ушакова
Жизнь и творчество Д.Н.Ушакова SELFLLERY Рынок цифровой фотографии
SELFLLERY Рынок цифровой фотографии Соблюдение лицензионных требований в сфере телерадиовещания
Соблюдение лицензионных требований в сфере телерадиовещания LR5_1ch__Stoimostnye_kharakteristiki_informatsionnoy_deyatelnosti
LR5_1ch__Stoimostnye_kharakteristiki_informatsionnoy_deyatelnosti Земля отцов – моя земля (из истории местных географических названий)
Земля отцов – моя земля (из истории местных географических названий) Движение
Движение Бораны и карбораны
Бораны и карбораны Время глагола
Время глагола походами ходили
походами ходили Компьютер Что это такое?
Компьютер Что это такое? Международный день чая
Международный день чая Декоративное убранство русского северного дома
Декоративное убранство русского северного дома Александр Солженицын
Александр Солженицын Совет единомышленников ГБОУ СОШ № 2001
Совет единомышленников ГБОУ СОШ № 2001