Вычисление площадей фигур на клетчатой бумаге

Аннотация.
На клетчатой бумаге с клетками размером 1 см 1 см изображены различные фигуры. Необходимо найти площадь. Ответ записать в квадратных сантиметрах.
Для того, чтобы быстро решать такие задания, надо знать формулы для вычисления площадей треугольника, прямоугольника, трапеции, параллелограмма, квадрата.
Часто при решении таких задач используются свойства площадей. Фигуру надо разбить на части, площади которых можно найти по знакомым формулам. Или наоборот, фигуру надо достроить. Получится большая фигура, площадь которой мы сможем найти.

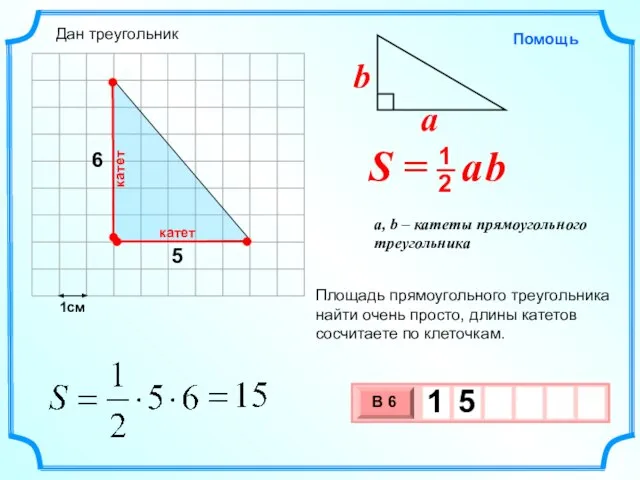
1см
5
6
Площадь прямоугольного треугольника найти очень просто, длины катетов сосчитаете по клеточкам.
Дан треугольник

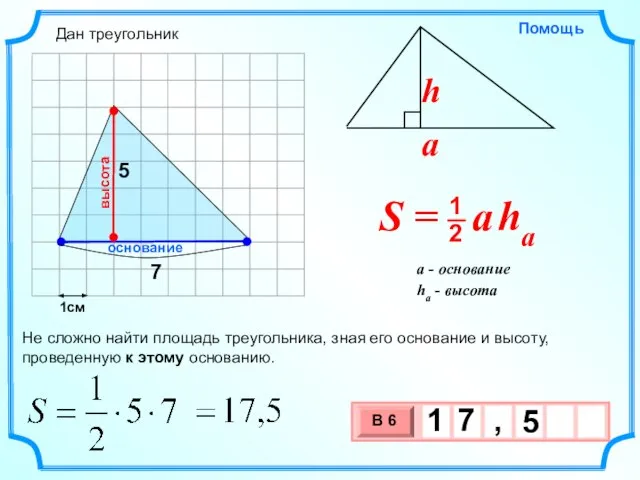
1см
5
Не сложно найти площадь треугольника, зная его основание и высоту, проведенную к этому основанию.
основание
высота
Дан треугольник

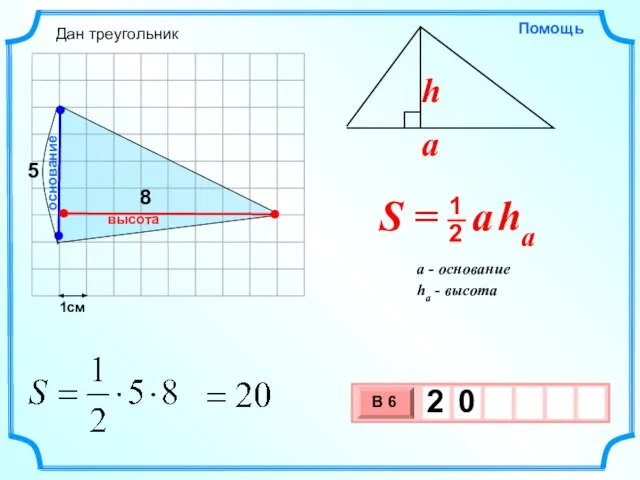
1см
8
основание
высота
Дан треугольник

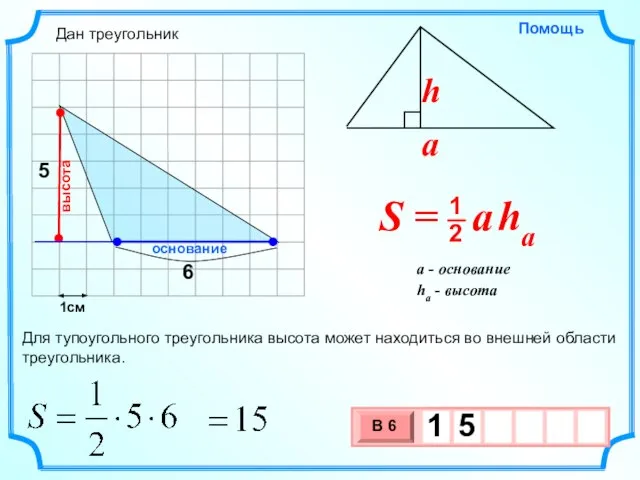
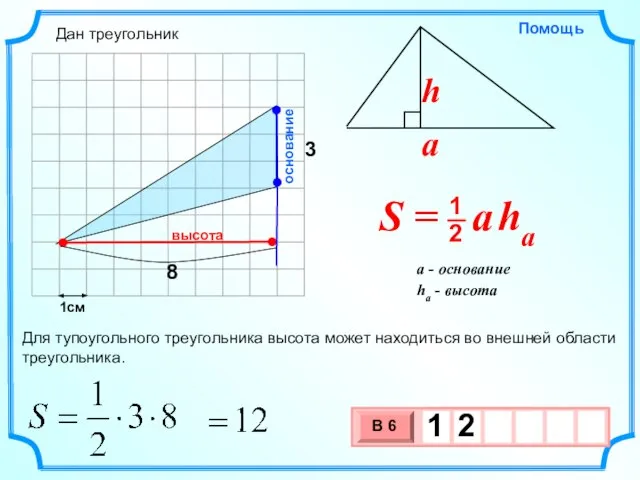
1см
основание
высота
Для тупоугольного треугольника высота может находиться во внешней области треугольника.
Дан треугольник

1см
3
основание
высота
Для тупоугольного треугольника высота может находиться во внешней области треугольника.
Дан треугольник

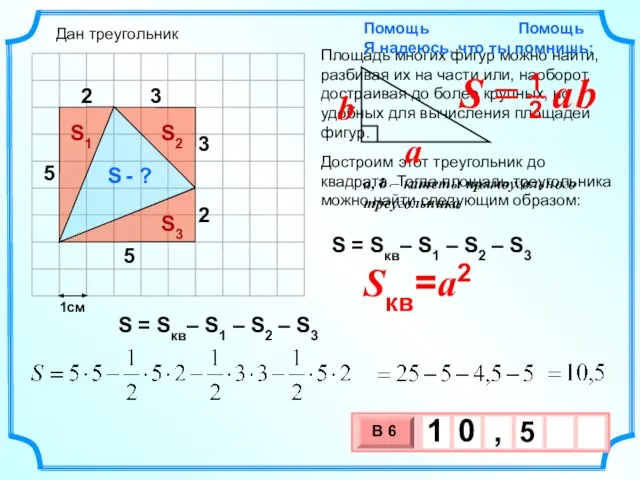
1см
S - ?
S = Sкв– S1 – S2 – S3
Дан треугольник

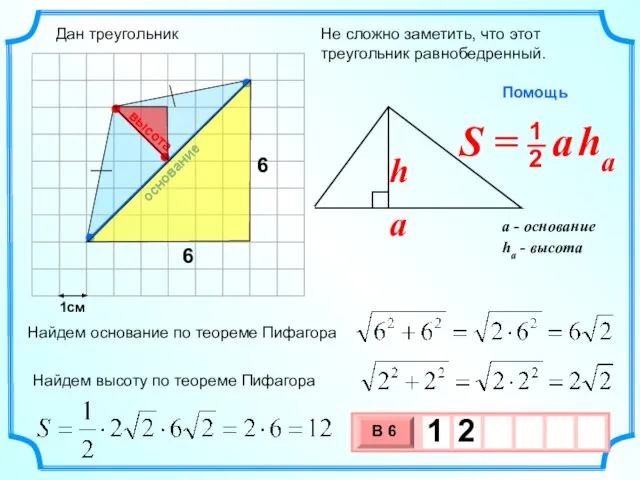
1см
Не сложно заметить, что этот треугольник равнобедренный.
Найдем основание по теореме Пифагора
Найдем высоту по теореме Пифагора
Дан треугольник

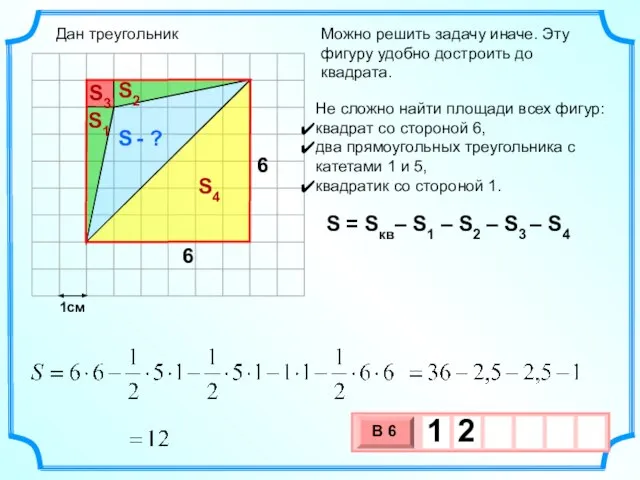
1см
Можно решить задачу иначе. Эту фигуру удобно достроить до квадрата.
Не сложно найти площади всех фигур:
квадрат со стороной 6,
два прямоугольных треугольника с катетами 1 и 5,
квадратик со стороной 1.
S - ?
S = Sкв– S1 – S2 – S3 – S4
Дан треугольник

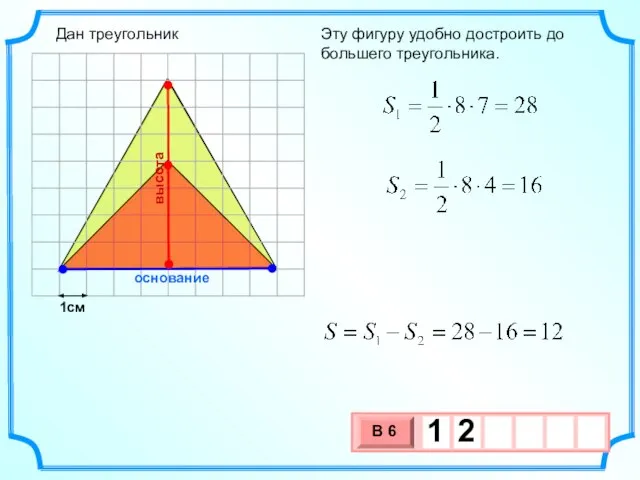
1см
Эту фигуру удобно достроить до большего треугольника.
основание
высота
Дан треугольник

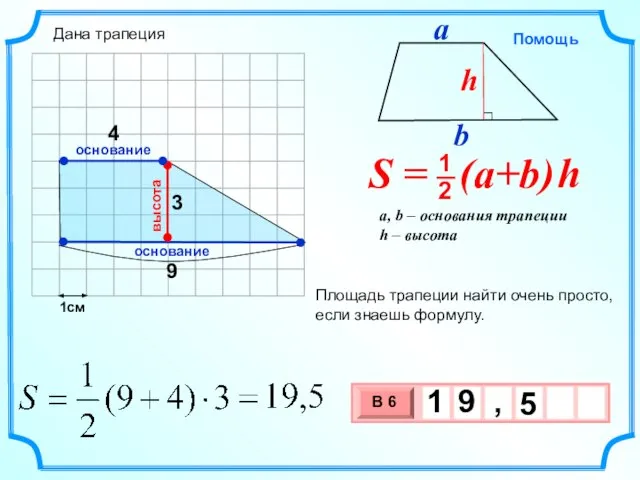
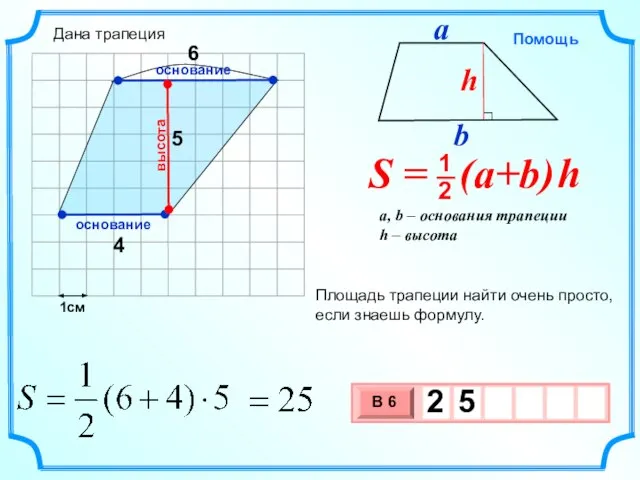
1см
9
3
Площадь трапеции найти очень просто, если знаешь формулу.
высота
основание
основание
4
Дана трапеция

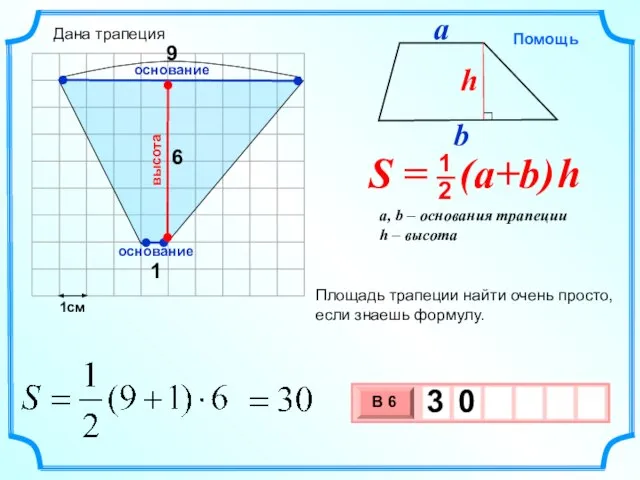
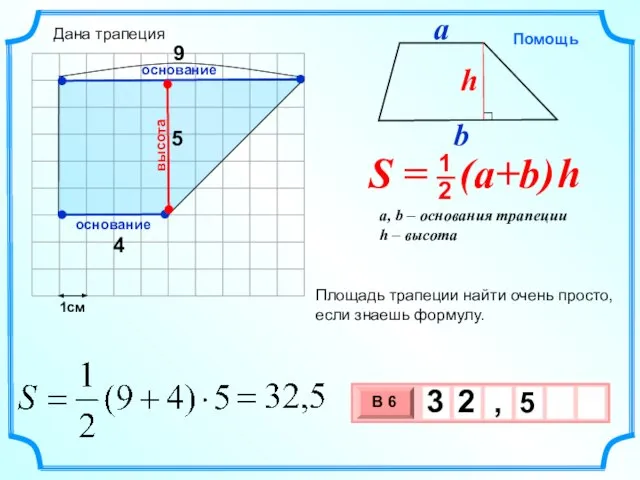
1см
1
6
Площадь трапеции найти очень просто, если знаешь формулу.
высота
основание
основание
9
Дана трапеция

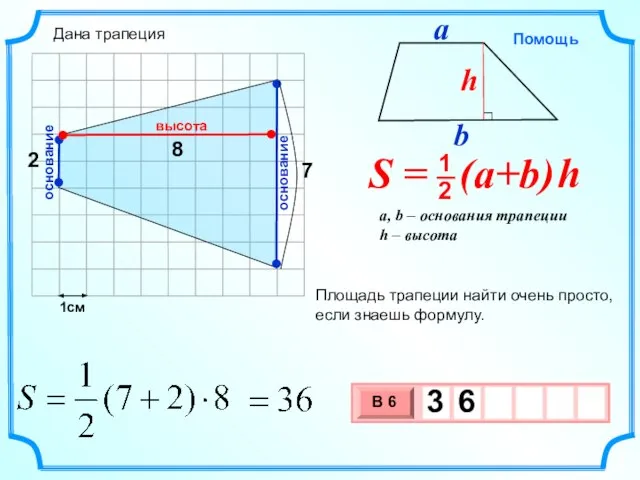
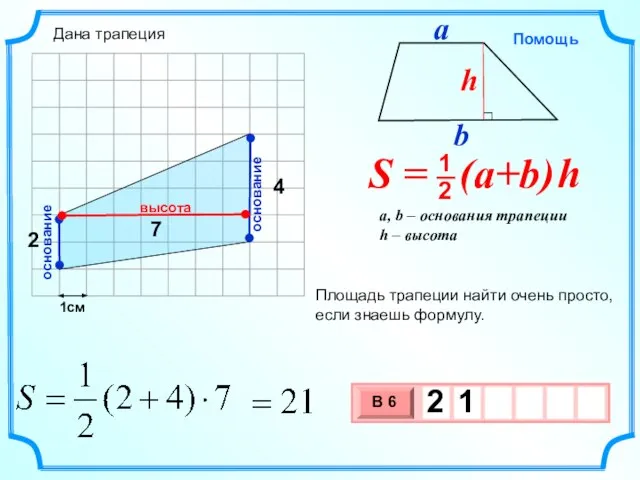
1см
7
8
Площадь трапеции найти очень просто, если знаешь формулу.
высота
основание
основание
2
Дана трапеция

1см
4
5
Площадь трапеции найти очень просто, если знаешь формулу.
высота
основание
основание
6
Дана трапеция

1см
4
5
Площадь трапеции найти очень просто, если знаешь формулу.
высота
основание
основание
9
Дана трапеция

1см
4
7
Площадь трапеции найти очень просто, если знаешь формулу.
высота
основание
основание
2
Дана трапеция

1см
Если на экзамене ты разволновался и забыл формулу для вычисления площади трапеции…
Выполним дополнительные построения так, чтобы получить фигуры, площади которых мы сможем вычислить.
S1
S2
S3
Ты получишь тот же ответ, но ты должен понимать, что потратишь больше времени!
А мне этот способ не понравился!

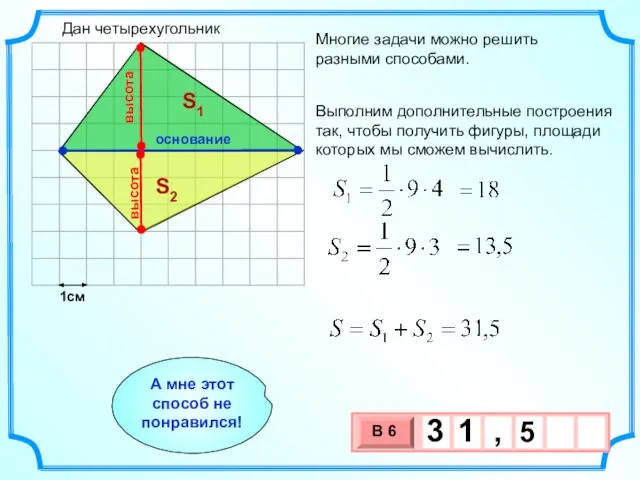
1см
Многие задачи можно решить разными способами.
S1
S2
Выполним дополнительные построения так, чтобы получить фигуры, площади которых мы сможем вычислить.
А мне этот способ не понравился!
Дан четырехугольник

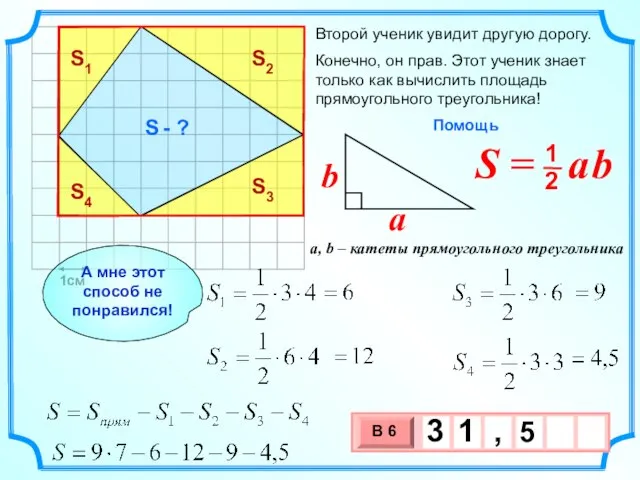
1см
Второй ученик увидит другую дорогу.
Конечно, он прав. Этот ученик знает только как вычислить площадь прямоугольного треугольника!
S - ?
S1
S2
S3
S4
А мне этот способ не понравился!

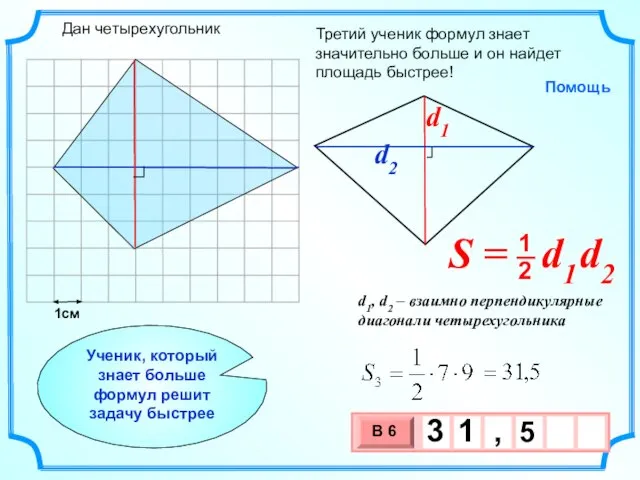
1см
Третий ученик формул знает значительно больше и он найдет площадь быстрее!
Ученик, который знает больше формул решит задачу быстрее
Дан четырехугольник

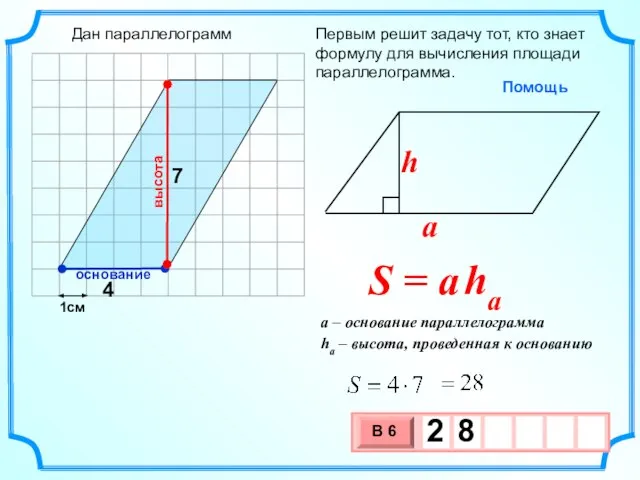
1см
Первым решит задачу тот, кто знает формулу для вычисления площади параллелограмма.
4
7
высота
основание
Дан параллелограмм

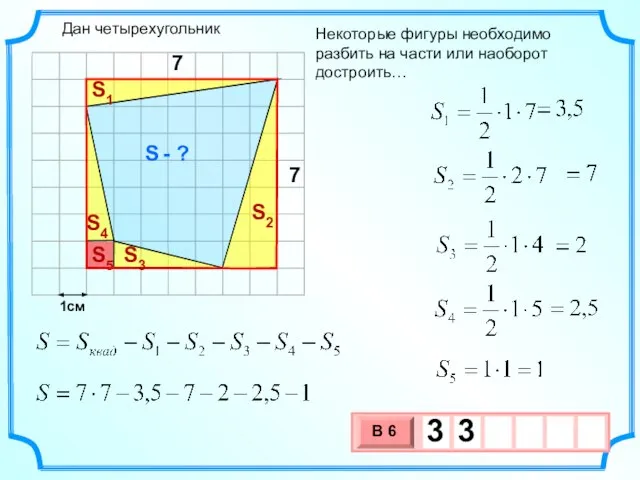
1см
Некоторые фигуры необходимо разбить на части или наоборот достроить…
S - ?
S1
S4
S2
S5
S3
Дан четырехугольник

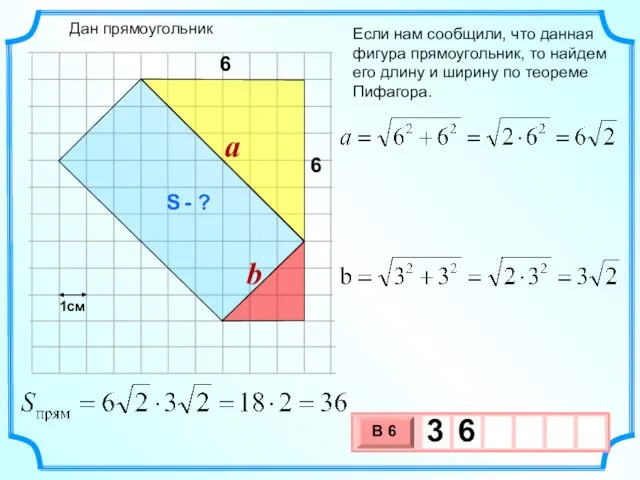
Если нам сообщили, что данная фигура прямоугольник, то найдем его длину и ширину по теореме Пифагора.
6
6
Дан прямоугольник
a
b
S - ?

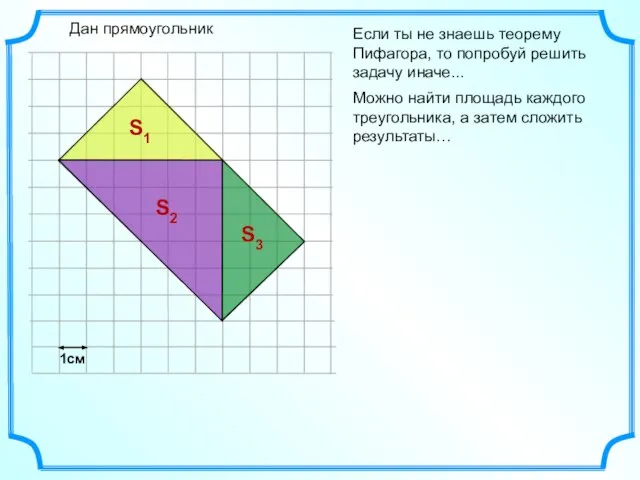
Если ты не знаешь теорему Пифагора, то попробуй решить задачу иначе...
Дан прямоугольник
1см
Можно найти площадь каждого треугольника, а затем сложить результаты…