Поверхности

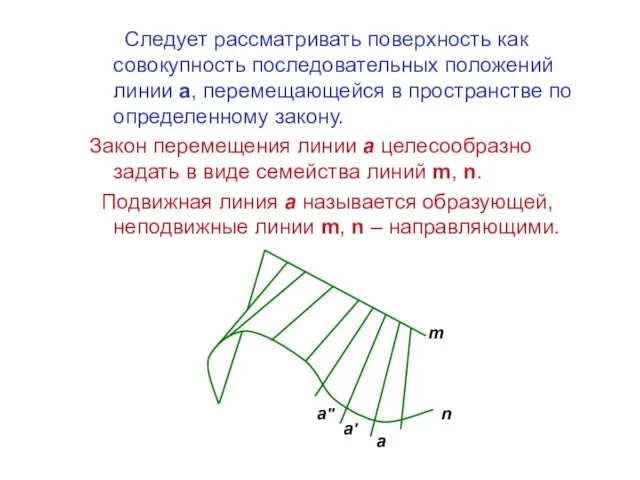
Следует рассматривать поверхность как совокупность последовательных положений линии a, перемещающейся в пространстве по определенному закону.
Закон перемещения линии а целесообразно задать в виде семейства линий m, n.
Подвижная линия а называется образующей, неподвижные линии m, n – направляющими.
m
n
a''
a
a'

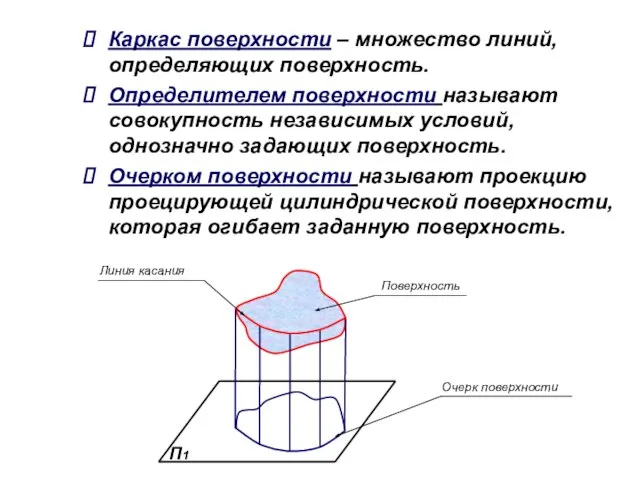
Каркас поверхности – множество линий, определяющих поверхность.
Определителем поверхности называют совокупность независимых условий, однозначно задающих поверхность.
Очерком поверхности называют проекцию проецирующей цилиндрической поверхности, которая огибает заданную поверхность.
П1
Очерк поверхности
Поверхность
Линия касания

Основой классификации поверхностей могут
служить их определители или геометрические
особенности, связанные с кинематическим
способом образования.
Важными признаками формообразования поверхностей являются:
Вид образующей;
Постоянство образующей;
Закон перемещения образующей;
Развёртываемость куска поверхности.

Классификация поверхностей
По виду образующей:
Линейчатые
Нелинейчатые
По постоянству образующей:
С постоянной образующей
С переменной образующей
По закону движения образующей:
Кинематические поверхности
Поверхности вращения
Винтовые поверхности
По развёртываемости:
Развёртываемые
Не развёртываемые

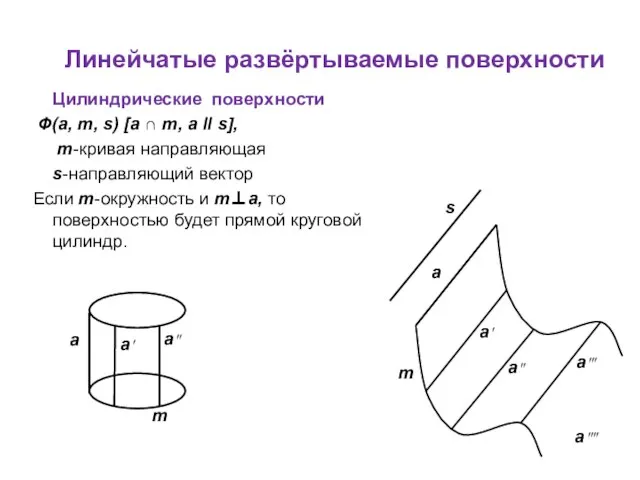
Линейчатые развёртываемые поверхности
Цилиндрические поверхности
Ф(a, m, s) [a ∩ m, a II s],
m-кривая направляющая
s-направляющий вектор
Если m-окружность и m⊥a, то поверхностью будет прямой круговой цилиндр.
m
a
s
a'
a''
a'''
a''''

Призматические поверхности
Ф(a, m, s) [a ∩ m, a II s]
m-ломаная линия
s-направляющий вектор
a
s
m
a'
a'''
a''

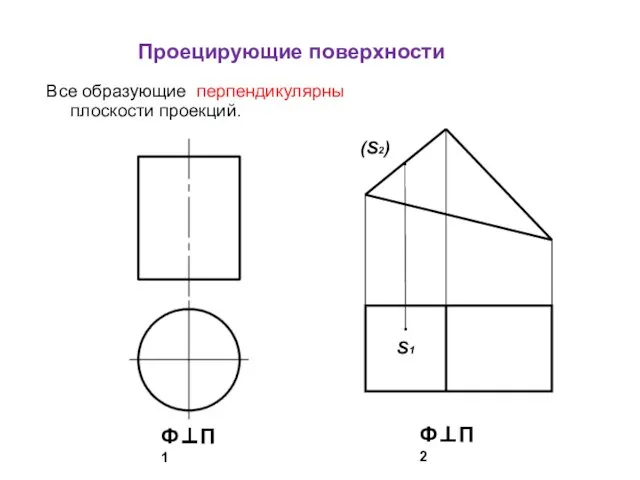
Проецирующие поверхности
Все образующие перпендикулярны плоскости проекций.
(S2)
S1
Ф⊥П 1
Ф⊥П 2

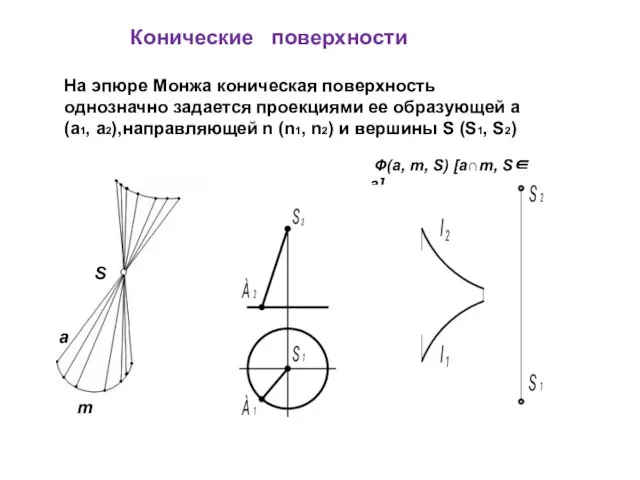
На эпюре Монжа коническая поверхность однозначно задается проекциями ее образующей a (a1, a2),направляющей n (n1, n2) и вершины S (S1, S2)
S
m
a
Конические поверхности
Ф(a, m, S) [a∩m, S∈ a]

Пирамидальные поверхности
S
a
m
a'
a''
a'''
Ф(a, m, S) [a∩m, S∈ a]

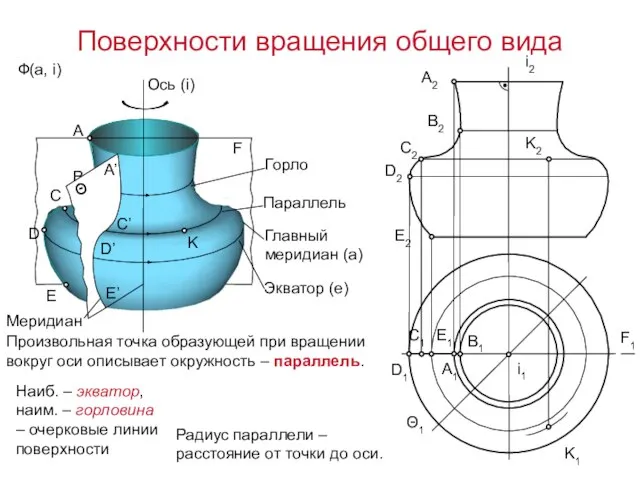
Поверхности вращения общего вида
Ф(а, i)
F1
Θ1
K1
K2
i2
Ось (i)
Произвольная точка образующей при вращении вокруг оси описывает окружность – параллель.
Радиус параллели – расстояние от точки до оси.
Наиб. – экватор, наим. – горловина – очерковые линии поверхности
i1
A2
B2
C2
D2
E2
E1
C1
D1
B1
A1
A
C
D
E
B
K
Параллель
F
Горло
Главный меридиан (а)
Экватор (е)
Меридиан
B’
C’
D’
E’
Θ
A’

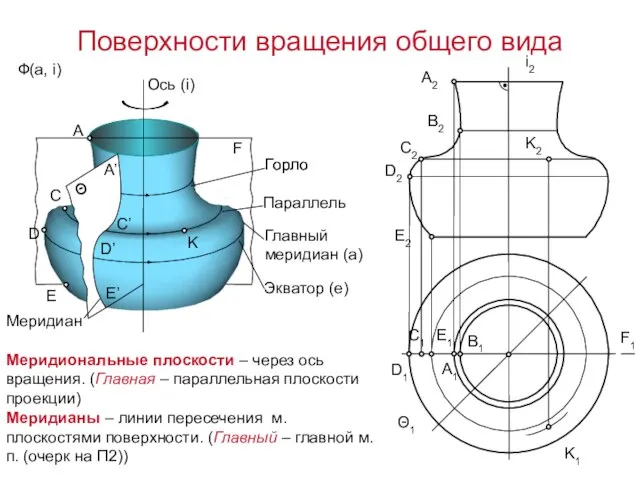
F1
Θ1
Меридиональные плоскости – через ось вращения. (Главная – параллельная плоскости проекции)
Меридианы – линии пересечения м. плоскостями поверхности. (Главный – главной м. п. (очерк на П2))
K1
K2
A2
B2
C2
D2
E2
E1
C1
D1
B1
A1
i2
Ф(а, i)
Ось (i)
A
C
D
E
K
Параллель
F
Горло
B’
C’
D’
E’
Θ
A’
Горло
Главный меридиан (а)
Экватор (е)
Меридиан
Поверхности вращения общего вида

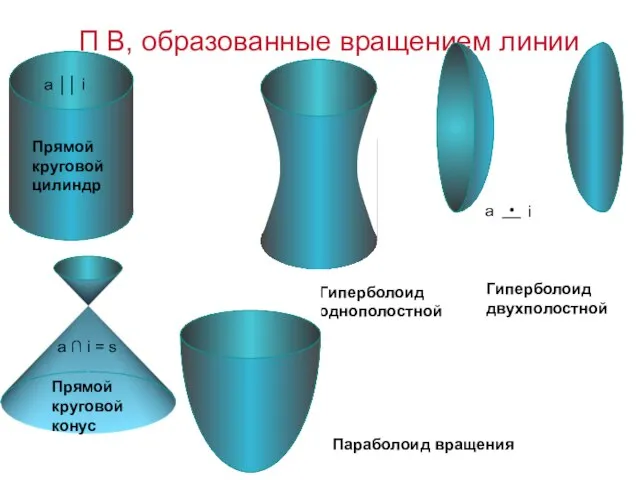
П В, образованные вращением линии
Прямой круговой конус
Гиперболоид однополостной
Параболоид вращения
Гиперболоид двухполостной
Прямой круговой цилиндр
a ∩ i = s
a ││ i

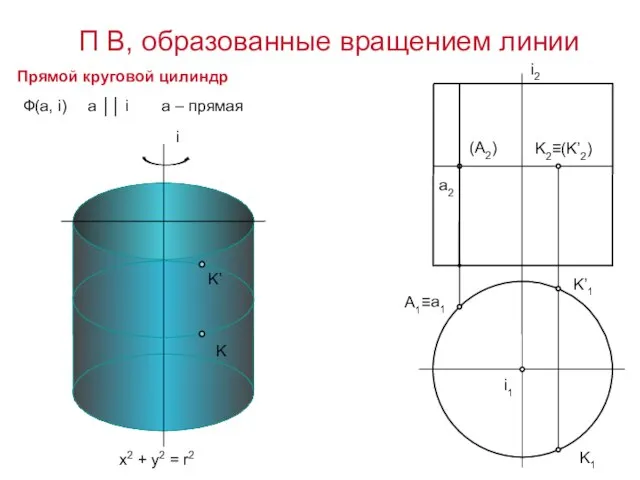
i
Ф(а, i)
a ││ i
Прямой круговой цилиндр
x2 + y2 = r2
а – прямая
K’1
i2
K2≡(K’2)
a2
(A2)
K1
i1
A1≡
П В, образованные вращением линии
a1

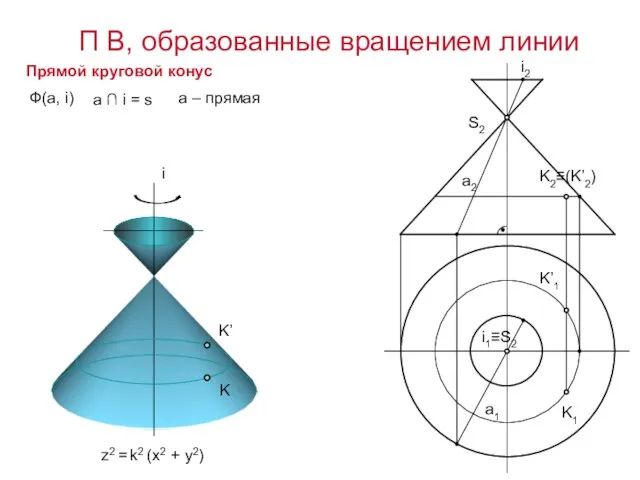
Ф(а, i)
a ∩ i = s
Прямой круговой конус
z2 = k2 (x2 + y2)
а – прямая
K1
K’1
i2
K2≡(K’2)
a1
a2
i1≡S2
S2
i
П В, образованные вращением линии

П В, образованные вращением окружности
Сфера
Тор закрытый
Тор открытый
t = 0
t ˂ R
t > R

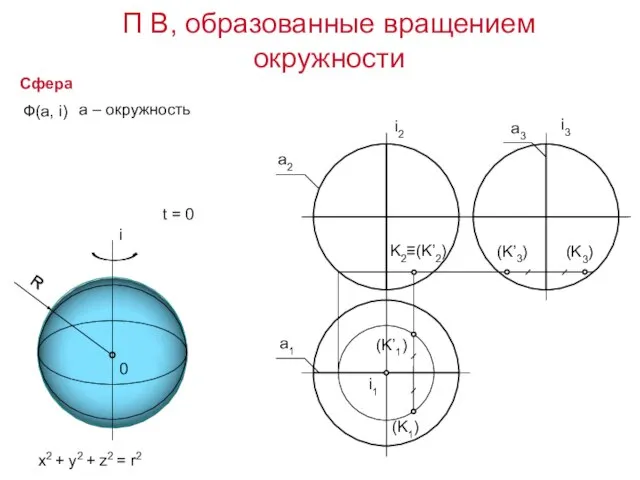
Сфера
x2 + y2 + z2 = r2
П В, образованные вращением окружности
Ф(а, i)
а – окружность
t = 0
i
i2
i1
(K1)
(K’1)
K2≡(K’2)
a1
i3
a3
a2
(K’3)
(K3)
0
R

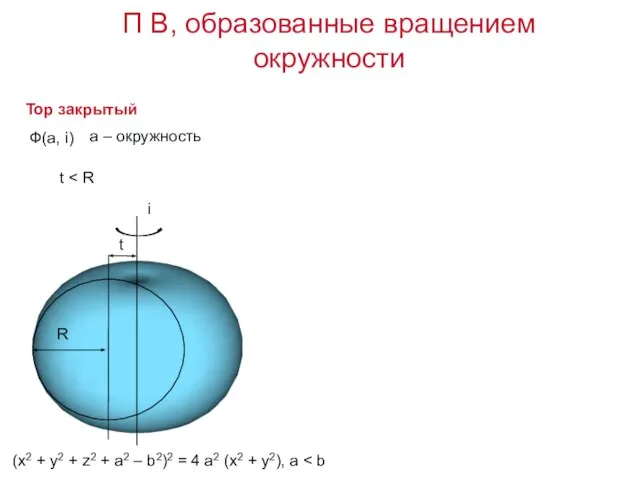
Тор закрытый
(x2 + y2 + z2 + a2 – b2)2 = 4 a2 (x2 + y2), a < b
t < R
Ф(а, i)
а – окружность
П В, образованные вращением окружности
i
t
0
R

Тор открытый
(x2 + y2 + z2 + a2 – b2)2 = 4 a2 (x2 + y2), a > b
Ф(а, i)
t > R
t
а – окружность
K’1
i2
K1
i1
K’’1
K’’’1
11
21
12
(22)
K2
П В, образованные вращением окружности
0
i
R

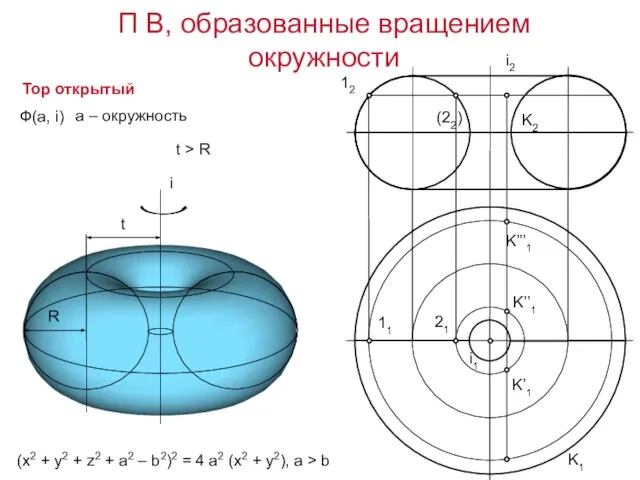
Эллипсоид вращения
a2(x2 + y2) + b2z2 = a2b2
сжатый
вытянутый
b2(x2 + y2) + b2z2 = a2b2
Закономерные поверхности вращения
Ф(а, i)
а – эллипс
i
i

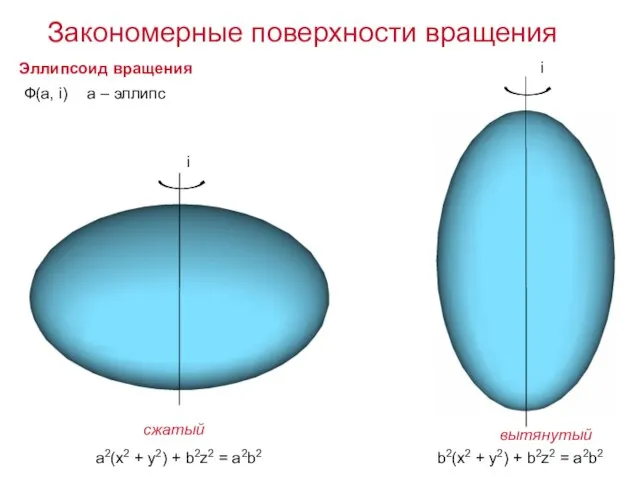
Ф(а, i)
Гиперболоид вращения
b2z2 – a2(x2 + y2) = a2b2
b2(x2 + y2) – a2z2 = a2b2
двухполостной
i
а – гипербола
i
однополостной