Содержание
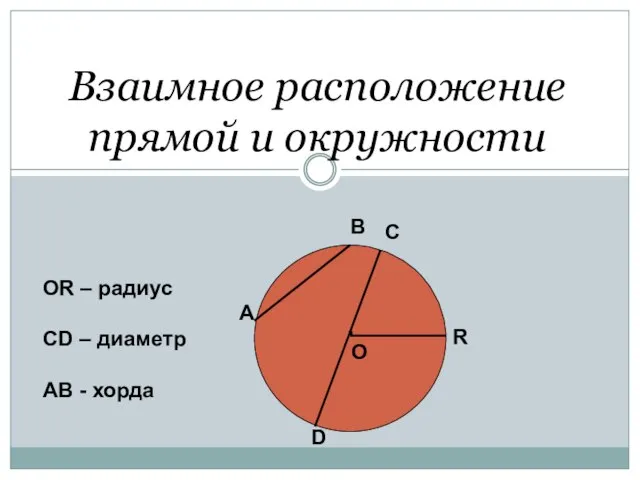
- 2. Взаимное расположение прямой и окружности . О А В С D R ОR – радиус СD
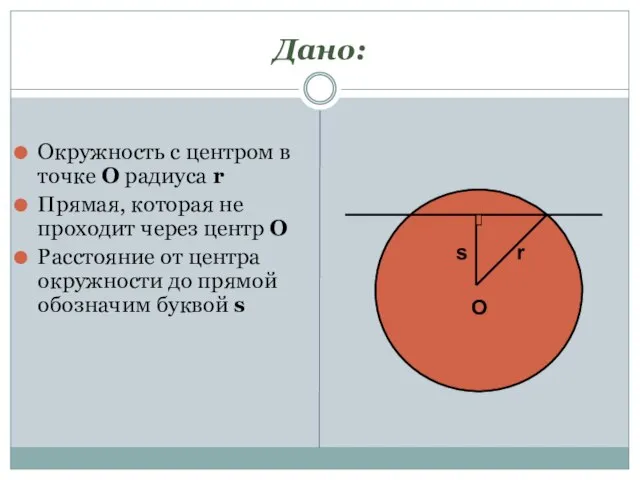
- 3. Дано: Окружность с центром в точке О радиуса r Прямая, которая не проходит через центр О
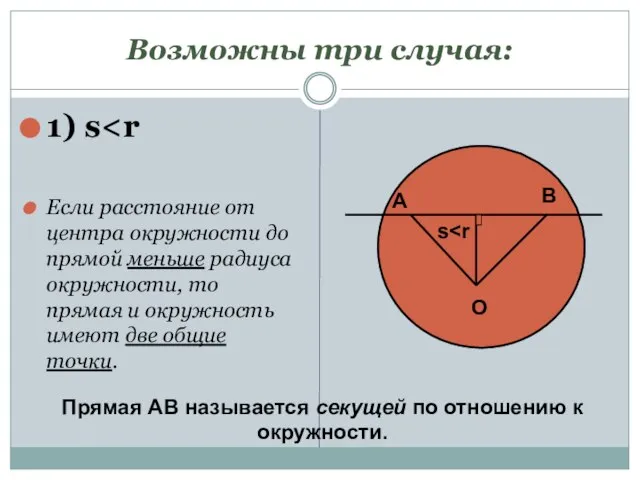
- 4. Возможны три случая: 1) s Если расстояние от центра окружности до прямой меньше радиуса окружности, то
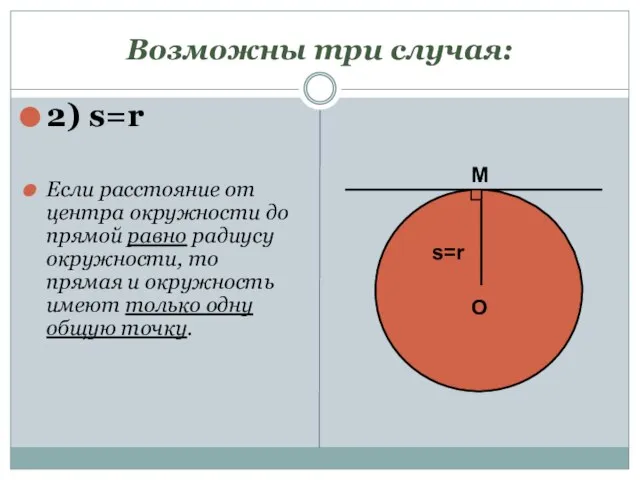
- 5. Возможны три случая: 2) s=r Если расстояние от центра окружности до прямой равно радиусу окружности, то
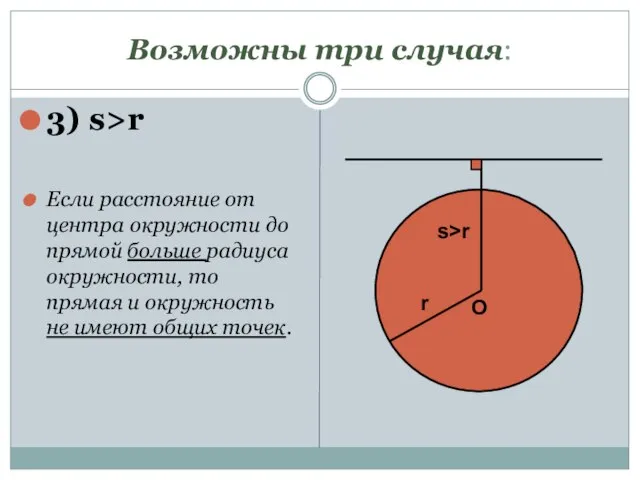
- 6. Возможны три случая: 3) s>r Если расстояние от центра окружности до прямой больше радиуса окружности, то
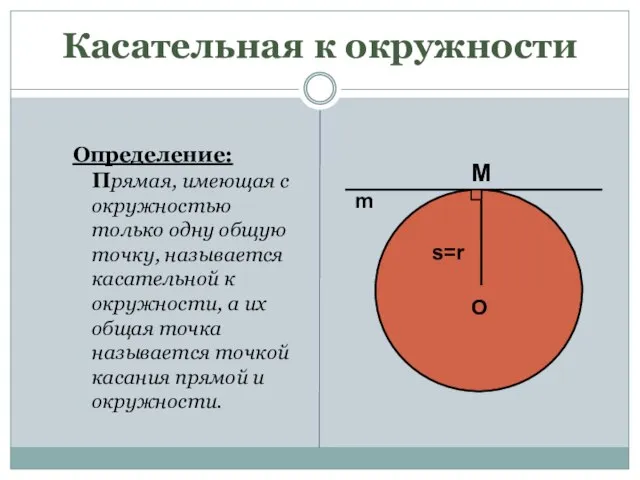
- 7. Касательная к окружности Определение: Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности,
- 8. Выясните взаимное расположение прямой и окружности, если: r = 15 см, s = 11см r =
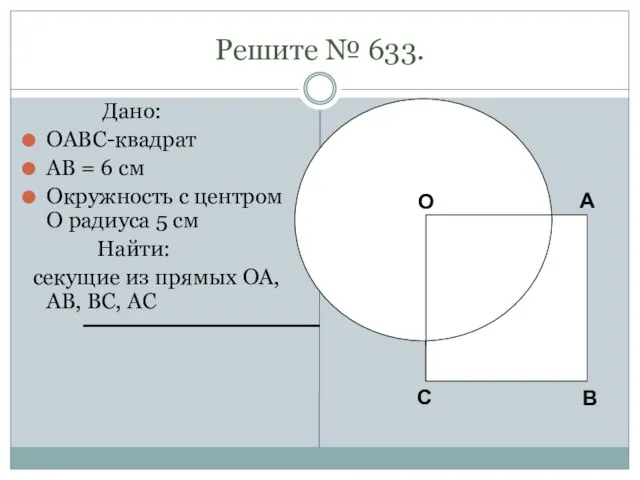
- 9. Решите № 633. Дано: OABC-квадрат AB = 6 см Окружность с центром O радиуса 5 см
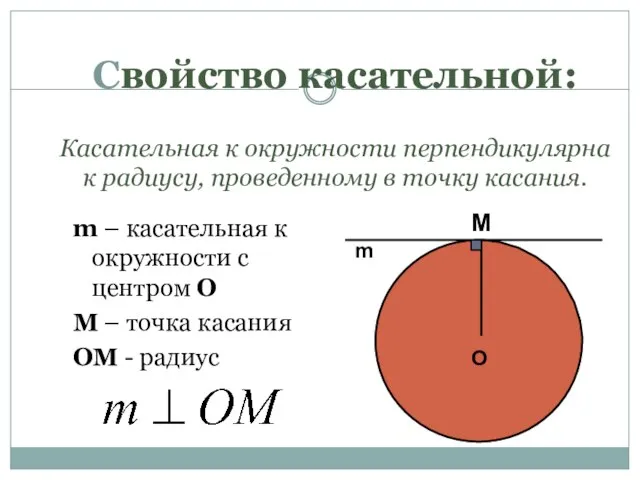
- 10. Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. m – касательная к
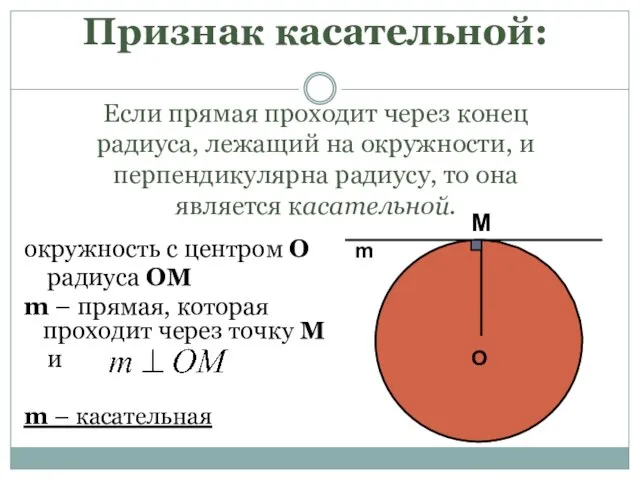
- 11. Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она
- 13. Скачать презентацию

 Сервис Мечты
Сервис Мечты Основи формування і реєстраціi корисного сигналу в діапазоні
Основи формування і реєстраціi корисного сигналу в діапазоні Комплексная система автоматизации
Комплексная система автоматизации Телепорт
Телепорт Осторожно! Сосульки
Осторожно! Сосульки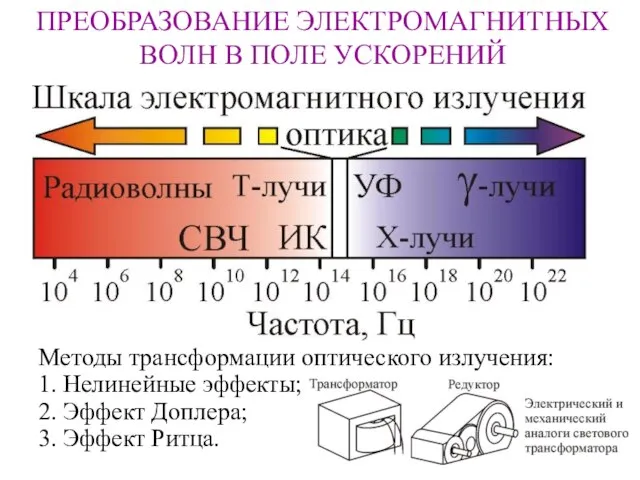 ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ
ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ Примеры комбинаторных задач (9 класс)
Примеры комбинаторных задач (9 класс) Решение логических задач из курса кибернетики
Решение логических задач из курса кибернетики Бедность
Бедность Nocturnal eczema: Review of sleep and circadian rhythms
Nocturnal eczema: Review of sleep and circadian rhythms Microsoft Office Word 2007
Microsoft Office Word 2007 Международное сотрудничество в освоении космического пространства
Международное сотрудничество в освоении космического пространства Золото
Золото Презентация на тему Загадки о диких животных
Презентация на тему Загадки о диких животных Королева оркестра
Королева оркестра Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина
Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар
Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар Образ Чичикова в поэме "Мертвые души"
Образ Чичикова в поэме "Мертвые души" Табір "Світанок"
Табір "Світанок" Презентация на тему Уфа – столица Башкортостана
Презентация на тему Уфа – столица Башкортостана Онтология
Онтология  Источники загрязнения окружающей среды
Источники загрязнения окружающей среды Project_A
Project_A Типы связи слов в словосочетании
Типы связи слов в словосочетании Всероссийский флешмоб Голубь мира
Всероссийский флешмоб Голубь мира Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во
Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во БИОСИНТЕЗ
БИОСИНТЕЗ Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12
Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12