Слайд 3Задача № 1
Каждая буква фрагмента известного стихотворения Ф.И. Тютчева заменена некоторой буквой так,

что разным буквам соответствуют разные буквы, а одинаковым - одинаковые. Пробелы и знаки препинания сохранены. Восстановите этот фрагмент стихотворения:
Гьюь Фюббшн эй яюэовл,
Пфзшэюь юришь эй шчьйфшвл:
Г эйщ юбюрйээпо бвпвл ⎯
С Фюббшн ьюцэю вюылъю сйфшвл.
Слайд 4Задача № 1
Гьюь Фюббшн эй яюэовл,
Пфзшэюь юришь эй шчьйфшвл:
Г эйщ юбюрйээпо бвпвл

⎯
С Фюббшн ьюцэю вюылъю сйфшвл.
Слайд 5Задача № 1 (ответ)
Умом Россию не понять,
Аршином общим не измерить:
У ней особенная

стать –
В Россию можно только верить.
Слайд 6Задача № 2
Криптоша изобрел устройство, которое позволяет вычислить среднее арифметическое любых

9 чисел или любых 223 чисел.
Слайд 7Задача №2 (продолжение)
Как правильно использовать это устройство, чтобы найти среднее арифметическое любых

2006 чисел.
При необходимости можно дополни-тельно провести одно деление и одно умножение.
Слайд 8Задача № 2 (решение)
Добавим к числам еще одно, равное нулю. Тогда

Слайд 11Задача № 3
Для зашифрования сообщения на английском языке составляются две таблицы размера

5x5. В клетки каждой таблицы в неизвестном порядке вписаны буквы укороченного английского алфавита (v и w отождествлены), так что каждая буква алфавита встречается в каждой таблице один раз.
Слайд 12Задача № 3
Букву, расположенную в i-ой строке и
j-м столбце первой таблицы обозначим

через аi j , а букву второй таблицы ⎯ через bi j . При зашифровании сообщение разбивается на пары подряд идущих букв.
Слайд 13Задача № 3
Пара вида аij blm заменяется:
при i ≠ l парой bim

alj ;
при i = l парой blj aim .
Слайд 14Задача № 3
В результате зашифрования сообщения
c r y p t o g

r a p h i c a l g o r i t h m
был получен один из следующих шифртекстов:
p a b d g l i u r c a v t h o t u e a d s p,
d s z q u p h s b q i j d b m h p s j u i n.
Определите, какой именно?
Слайд 15Задача № 3 (решение)
Способ зашифрования текста обладает свойством:
Если пара ab заменяется на

пару cd,
то пара dc перейдет в пару ba.
a c d b
Слайд 16Задача № 3 (решение)
ОТКРЫТЫЙ ТЕКСТ
сr yp to gr ap hi ca lg

or it hm
рa bd gl iu rc av th ot ue ad sp
ПЕРВЫЙ ШИФРТЕКСТ
противоречащих свойству пар нет
Слайд 17Задача №3 (решение)
ОТКРЫТЫЙ ТЕКСТ
сr yp to gr ap hi ca lg or

it hm
ds zq up hs bq ij db mh ps ju in
ВТОРОЙ ШИФРТЕКСТ
есть противоречащие свойству пары
Слайд 18Задача № 4
Пусть a1, a2, a3, … и b1, b2, b3, …

последовательности периодов 16 и 2006 соответственно. Найдите период последовательности
a1, b1, a2, b2, a3, b3, …
Периодом x1, x2,… называется наимень-шее натуральное число T, что для всех натуральных n верно равенство
xn+T = xn
Слайд 19Задача № 4 (решение)
Разобьём последовательность {xn} на пары
(х1,х2), (х3,х4), …
(a1,b1), (a2,b2),

…
Период этой последовательности пар равен c=НОК(16,2006)=16048.
Слайд 20Задача № 4 (решение)
При всех натуральных n верно равенство
xn=xn+2с

Слайд 21Задача № 4 (решение)
При всех натуральных n верно равенство
xn=xn+2с
Покажем, что 2с –

наименьшее число с таким условием.
Слайд 22Задача № 4 (решение)
При всех натуральных n верно равенство
xn=xn+2с
Покажем, что 2с –

наименьшее число с таким условием.
Пусть период последовательности {xn} равен t. Тогда число 2c должно делиться на число t.
Слайд 23Задача № 4 (решение)
Случай 1. Пусть t нечетно.
Тогда первая последовательность является

«сдвигом» второй, что противоречит различию длин их периодов.
Слайд 24Задача № 4 (решение)
Случай 2. Пусть t четно, t =2k.
Тогда

для всех m выполнено
x2m-1+t = x2m-1
x2m+t = x2m
Отсюда
am+k=am
bm+k=bm
Слайд 25Задача № 4 (решение)
Таким образом, k делится на НОК периодов исходных последователь-ностей.
Отсюда

t = 2НОК(16, 2006) = 32096.
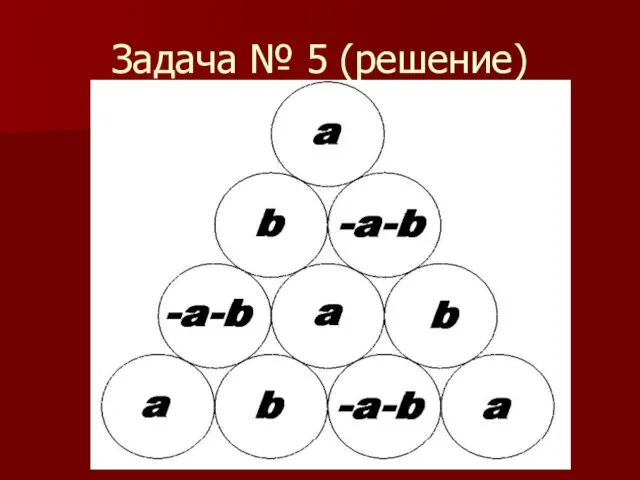
Слайд 26Задача № 5
Бильярдные шары плотно уложены в правильный треугольник с основа-нием из

2006 шаров. На каждом шаре написано число. Сумма трех чисел на шарах при вершинах исход-ного треугольника, а также любых треугольников со сторонами, парал-лельными исходному треугольнику, равна 0. Какие числа могут быть написаны на шарах?
Слайд 28Задача № 6
Заполните неокрашенные клетки таблицы числами от 1 до 9.

При этом, сумма цифр в каждой горизонтальной неокрашенной цепочке должна совпадать с числом, указанным слева от цепочки, а в каждой вертикальной неокрашенной цепочке - с числом, указанным сверху от цепочки.
В каждой цепочке ни одна цифра не должна повторяться.
Слайд 30Задача № 6 (решение)
Единственно возможное заполнение таблицы

Слайд 32С задачами прошедших олимпиад и их решениями можно познакомиться:
на сайте Академии www.academy.fsb.ru

на сайте www.cryptography.ru (раздел занимательная криптография)
в книге «Введение в криптографию» МЦНМО, 2002.
в книге «Олимпиады по криптографии и математике для школьников»
МЦНМО, 2006.
Слайд 33 Связаться с оргкомитетом олимпиад можно по электронной почте
Olymp @ academy.fsbOlymp @

academy.fsb.ru
Подписку на рассылку информации оргкомитета можно оформить, отправив на этот адрес письмо с темой SUBSCRIBE.
Тел. 931-34-22
Слайд 34Мероприятия для школьников в 2007 году
Окружной тур олимпиады по математике
28 января

(воскресенье)
Окружной тур олимпиады по физике
3 февраля (суббота)
Региональная олимпиада по математике
25 февраля (воскресенье)
Слайд 35Мероприятия для школьников в 2007 году
Победителям этих олимпиад предоставляются льготы при поступлении

в ИКСИ и ряд других вузов.
Слайд 36Мероприятия для школьников в 2007 году
Собеседования
(для школьников 10 класса)
март, май
по предварительной

записи
Слайд 37Мероприятия для школьников в 2007 году
Письменные работы по математике и физике
октябрь

Слайд 38Мероприятия для школьников в 2007 году
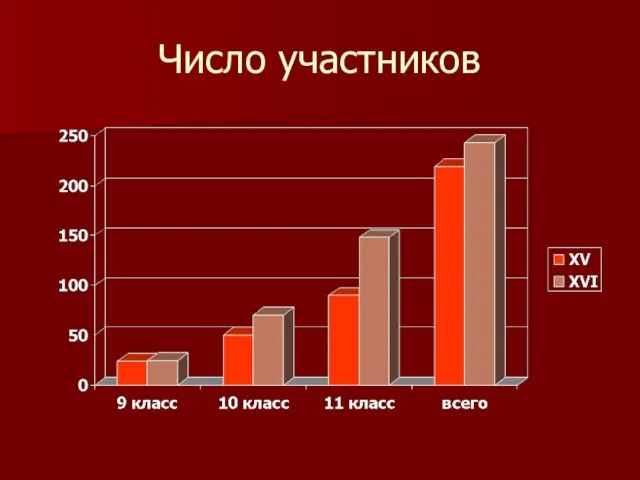
XVII Олимпиада по математике и криптографии
в

конце ноября или начале декабря



































 Новый менеджер в сформировавшейся команде – методы безболезненного внедрения Вершинина Екатерина
Новый менеджер в сформировавшейся команде – методы безболезненного внедрения Вершинина Екатерина SPE Outstanding Student Chapter and Gold Award Criteria
SPE Outstanding Student Chapter and Gold Award Criteria Предлог
Предлог Презентация на тему Физминутка для глаз
Презентация на тему Физминутка для глаз  Теплота згоряння палива. Розрахунок кількості теплоти внаслідок згоряння палива
Теплота згоряння палива. Розрахунок кількості теплоти внаслідок згоряння палива Вакцины от ВПЧ. Конкурентная борьба и стратегия работы врача женской консультации.Нужна ли нам государственная программа вакцина
Вакцины от ВПЧ. Конкурентная борьба и стратегия работы врача женской консультации.Нужна ли нам государственная программа вакцина Египетские пирамиды в Гизе
Египетские пирамиды в Гизе О дисциплинах цикла ГСЭ
О дисциплинах цикла ГСЭ Проект для сотрудников (шаблон)
Проект для сотрудников (шаблон) «Работа учреждения в рамках реализации закона 83-ФЗ»
«Работа учреждения в рамках реализации закона 83-ФЗ» Карикатурный портрет
Карикатурный портрет Am, is or are
Am, is or are ДОКЛАД: М.М. ТУЛЯГАНОВОЙ ОСОБЕННОСТИ НЕФОРМАЛЬНОЙ ЭКОНОМИКИ В РЕСПУБЛИКЕ УЗБЕКИСТАН
ДОКЛАД: М.М. ТУЛЯГАНОВОЙ ОСОБЕННОСТИ НЕФОРМАЛЬНОЙ ЭКОНОМИКИ В РЕСПУБЛИКЕ УЗБЕКИСТАН Кленовый лист, кленовый лист, ты мне среди зимы приснись
Кленовый лист, кленовый лист, ты мне среди зимы приснись Путешествия в сказку
Путешествия в сказку Визитная карточка школы
Визитная карточка школы ОПЕРАТИВНАЯ ПОЛИГРАФИЯ
ОПЕРАТИВНАЯ ПОЛИГРАФИЯ Учебный проектОсновные темы рассказа А.И. Куприна «Белый пудель»
Учебный проектОсновные темы рассказа А.И. Куприна «Белый пудель» London. Sightseeing of London
London. Sightseeing of London Документы и сведения, представляемые таможенным органам при прибытии на таможенную территорию Подготовили: студентки 3-го курса
Документы и сведения, представляемые таможенным органам при прибытии на таможенную территорию Подготовили: студентки 3-го курса  Логічні одиниці інформаціи
Логічні одиниці інформаціи Основы ЭКГ
Основы ЭКГ Английская монархия от завоевания до парламента
Английская монархия от завоевания до парламента Налоги. Объект налогообложения
Налоги. Объект налогообложения Освещение. Свет и тень. Правила распределения светотени в натюрморте
Освещение. Свет и тень. Правила распределения светотени в натюрморте Презентация "Художественный образ в произведениях музыки и изобразительного искусства" - скачать презентации по МХК
Презентация "Художественный образ в произведениях музыки и изобразительного искусства" - скачать презентации по МХК Учитель начальных классов высшей категории МОУ «СОШ №6» г. Бузулука Оренбургской области
Учитель начальных классов высшей категории МОУ «СОШ №6» г. Бузулука Оренбургской области Организация и планирование закупок. Тема 2
Организация и планирование закупок. Тема 2