Задачи, приводящие к понятию производной

В начале было слово.
К понятию производной можно прийти, рассматривая, например, такое широко используемое в физике понятие, как мгновенная скорость неравномерно движущегося тела.
Мы познакомились с этим понятием, изучая в курсе физики раздел кинематики, а точнее кинематики прямолинейного неравномерного движения.

Совершенно верно. Как же Вы представляете себе мгновенную скорость? Что это такое?
Мгновенной скоростью тела называют скорость, которую оно имеет в данный момент времени (в данной точке траектории)

А как Вы представляете себе мгновенную скорость?
Так и представляю… Если тело движется равномерно, то в разные моменты времени его скорость одинакова. Если тело движется неравномерно (ускоряясь или замедляясь, то в разные моменты времени его скорость будет, вообще говоря, различной

Разве Вы не чувствуете, что фраза «скорость в данный момент времени» не более как синоним фразы «мгновенная скорость»? Как говорится, «что в лоб, что по лбу». Термин «скорость в данный момент времени нуждается в разъяснении в той же мере, в какой нуждается в нём термин «мгновенная скорость».
Физик эту проблему решает просто. У него есть приборы, например, спидометр. А математик создаст математическую модель процесса.
Итак, проблема поставлена.
Приступим к её решению.

Остановись мгновенье –
мы тебя исследуем !
Сначала мы определили «территорию» своих исследований. В каких ещё науках математика поможет решить подобную проблему ?
Оказалось, что связь между количественными характеристиками самых различных процессов, исследуемых физикой, химией, биологией, экономикой, техническими науками, аналогична связи между путём и скоростью.
Основным математическим понятием, выражающим эту связь является производная.

Производная
Центральные понятия дифференциального исчисления – производная и дифференциал возникли при рассмотрении большого числа задач естествознания и математики, приводивших к вычислению пределов одного и того же типа. Важнейшие среди них – физическая задача определения скорости неравномерного движения и геометрическая задача построения касательной к кривой.
Рассмотрим подробно каждую из них.

Будем вслед за итальянским учёным Г.Галилеем изучать закон свободного падения тел. Поднимем камешек и затем из состояния покоя отпустим его. Движение свободно падающего тела явно неравномерное. Скорость v постепенно возрастает. Но как именно выглядит зависимость v(t) ?

Фиксируем момент t, в который мы хотим знать значение скорости v(t). Пусть h – небольшой промежуток времени, прошедший от момента t. За это время падающее тело пройдёт путь, равный s(t+h)-s(t).
Если промежуток времени h очень мал, то приближённо
s(t+h)-s(t)≈v(t)∙h, или , причём
последнее приближённое равенство тем точнее, чем меньше h. Значит величину v(t) скорости в момент t можно рассматривать как предел, к которому стремится отношение, выражающее среднюю скорость на интервале времени от момента t до момента t+h.
Сказанное записывают в виде

Задача о мгновенной скорости
Предел средней скорости за промежуток времени от t0 до t при t→ t0, называется мгновенной скоростью v(t0) в момент времени t0
v(t0) =

А л г о р и т м
∆t = t – t0 ∆x = x – x0
∆v = v(t+t0) - v(t0) ∆f = f(x+x0) – f(x0)
.
.
На языке предмета На математическом языке

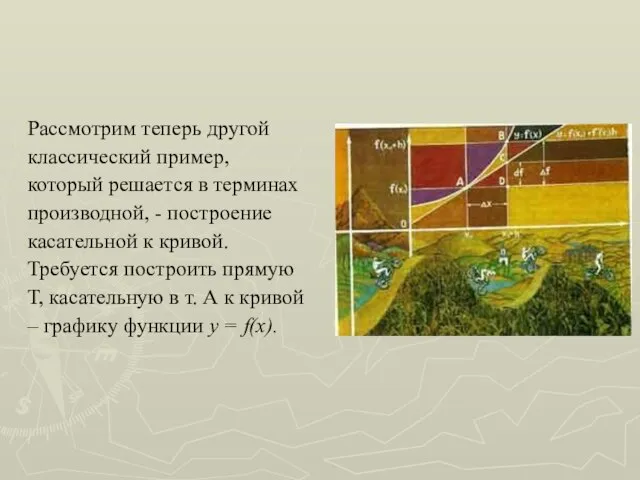
Рассмотрим теперь другой классический пример, который решается в терминах производной, - построение касательной к кривой. Требуется построить прямую Т, касательную в т. А к кривой – графику функции y = f(x).

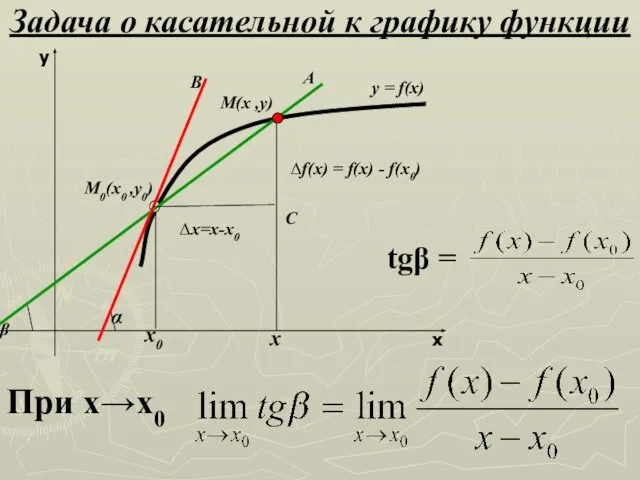
Задача о касательной к графику функции
x
y
С
∆х=х-х0
∆f(x) = f(x) - f(x0)

А л г о р и т м
1) ∆x = x – x0
2) ∆f = f(x+x0) – f(x0)
3)
4)

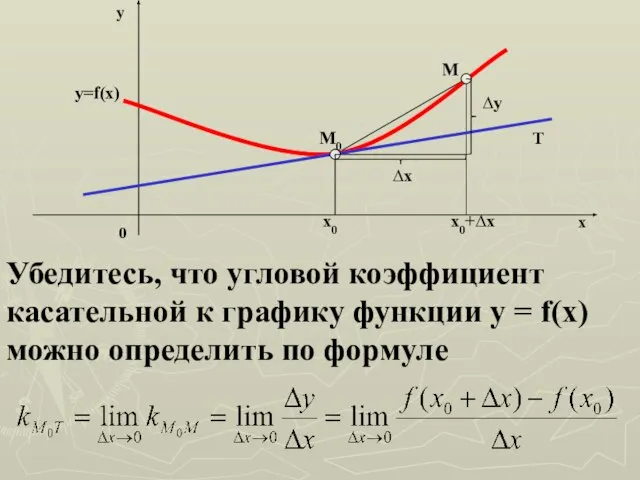
y=f(x)
M0
M
T
x0 x0+∆x
∆x
∆y
y
x
0
Убедитесь, что угловой коэффициент касательной к графику функции y = f(x) можно определить по формуле

Задача о скорости химической реакции
Средняя скорость растворения соли в воде за промежуток времени [t0;t1] (масса соли, растворившейся в воде изменяется по закону х = f(t)) определяется по формуле .
Скорость растворения в данный момент времени

А л г о р и т м
∆t = t – t0 ∆x = x – x0
∆f = f(t1) - f(t0) ∆f = f(x) – f(x0)
.
.
На языке предмета На математическом языке

Задача о теплоёмкости тела
Если температура тела с массой в 1 кг повышается от t1 = 0
до t2 = τ, то это происходит за счёт того, что телу сообщается определённое количество тепла Q; значит Q есть функция температуры τ, до которой тело нагревается: Q=Q(τ).
Пусть температура повысилась с τ до τ +Δτ. Количество тепла ΔQ, затраченное для этого нагревания равно: ΔQ=Q(τ+Δτ)-Q(τ).
Отношение есть количество тепла,
которое необходимо «в среднем» для нагревания тела на 1°. Это отношение называется средней теплоёмкостью, которая не даёт представления о теплоёмкости для любого значения температуры τ.
Теплоёмкостью при температуре τ называ-ется предел отношения приращения количества тепла ΔQ к приращению температуры Δτ.( при Δτ →0)

∆τ = τ – τ0 ∆x = x – x0
∆Q = Q(τ1) - Q(τ0) ∆f = f(x) – f(x0)
.
.
А л г о р и т м
На языке предмета На математическом языке

Задача о мгновенной величине тока
Обозначим через q = q(t) количество электричества, протекающее через поперечное сечение проводника за время t.
Пусть Δt – некоторый промежуток времени, Δq = q(t+Δt) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока.
Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt→0.

∆t = t – t0 ∆x = x – x0
∆q = q(t1) - q(t0) ∆f = f(x) – f(x0)
.
.
А л г о р и т м
На языке предмета На математическом языке

Экономические задачи
Рассмотрим ситуацию: пусть y - издержки производства, а х - количество продукции, тогда Δx- прирост продукции, а Δy - приращение издержек производства.
В этом случае производная выражает предельные
издержки производства и характеризует приближенно дополнительные затраты на производство дополнительной
единицы продукции ,где MC – предельные
издержки (marginal costs); TC – общие издержки (total costs); Q - количество.C(t)СС

Аналогичным образом могут быть определены и многие другие экономические величины, имеющие предельный характер.
Другой пример - категория предельной выручки
(MR— marginal revenue) — это дополнительный доход, полученный при переходе от производства n-ной к (n+1)-ой единице продукта.
Она представляет собой первую производную от выручки:
При этом R= PQ, где R–выручка (revenue); P–цена (price).
Таким образом , ⇒ MR= P.
Экономические задачи

Экономические задачи
Пусть функция u(t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент t0.
За период от t0 до t0+ t количество продукции изменится от u(t0) до u0+Δ u = u(t0+Δ t). Тогда средняя
производительность труда за этот период
поэтому производительность труда в момент t0

Рост численности населения
Вывести формулу для вычисления численности населения на ограниченной территории в момент времени t.
Пусть у=у(t)- численность населения.
Рассмотрим прирост населения за Δt = t - t0
Δy=k ∙ y ∙ Δt, где к = кр – кс –коэффициент прироста (кр – коэффициент рождаемости,
кс – коэффициент смертности)
получим

Выводы
Различные задачи привели в процессе решения к одной и той же математической модели – пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Значит, эту математическую модель надо специально изучить, т.е.:
Присвоить ей новый термин.
Ввести для неё обозначение.
Исследовать свойства новой модели.
Определить возможности применения нового понятия - производная

Определение производной
Производной функции f(x) в точке х называется предел отношения приращения функции в точке х к приращению аргумента, когда приращение аргумента стремится к нулю, если этот предел существует

Возвращаясь к рассмотренным задачам, важно подчеркнуть следующее:
а) мгновенная скорость неравномерного движения есть производная от пути по времени;
б) угловой коэффициент касательной к графику функции в точке (x0; f(x)) есть производная функции f(x) в точке х = х0;
в) мгновенная сила тока I(t) в момент t есть производная от количества электричества q(t) по времени;
г) теплоёмкость С(τ) при температуре τ есть производная от количества тепла Q(τ), получаемого телом;
д) скорость химической реакции в данный момент времени t есть производная от количества вещества у(t), участвующего в реакции, по времени t.

А это значит:
Аппарат производной можно использовать при решении геометрических задач, задач из естественных и гуманитарных наук, экономических задач оптимизационного характера.
И, конечно, не обойтись без производной при исследовании функции и построении графиков, решении уравнений и неравенств
У нас впереди огромные возможности для исследовательской работы в новых проектах!
«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский