Содержание
- 2. РАЗМИНКА 1 вариант Докажите, что 102009 + 8 кратно 9. 2 Вариант. Доказать, что разность трёхзначного
- 3. 1 вариант. Признак делимости на 9 – сумма цифр в числе делится на 9. 102009 +
- 4. Доказать, что при любом чётном n число n³+20n делится на 48. ЗАДАЧА №1
- 5. n=2к n³+20n= 8к(к2+5)кратно 8 к(к2+5)=к3-к+6к= (к-1)к(к+1) +6к 6к кратно 6 (к-1)к(к+1) кратно 6 Следовательно n³+20n кратно
- 6. Сумма трех целых чисел делится на 6. Доказать, что и сумма кубов этих чисел делится на
- 7. х3+у3+z3-(х + у +z) делится на 6. х3-х, у3-у, z3-z (делятся на 6) х3-х=х(х2-1)= х(х-1)(х+1) РЕШЕНИЕ.
- 8. Доказать, что ни при каком натуральном n число n2 +1 не делится на 3 ЗАДАЧА №3.
- 9. Метод полной индукции: n=3к, то n2 +1=9к2+1 (при делении на 3 остаток1) n=3к+1, то n2 +1=9к2+6к+2
- 10. Докажите, что значение выражения 116+146-133 кратно 10. ЗАДАЧА №4
- 11. 116 оканчивается на 1. 146 оканчивается на 6. 133 оканчивается цифрой 7. 116+146-133 оканчивается на0, следовательно
- 12. Найдите два натуральных числа, сумма которых равна 168, а их наибольший общий делитель равен 24. ЗАДАЧА
- 13. а+в=168, где а=24n1, в=24n2, где n1 и n2натуральные числа. 24n1+24n2=168 n1+n2=7 а=24,48,72; в=144, 120,96. РЕШЕНИЕ.
- 14. Сколько делителей у числа 1010? ЗАДАЧА №6
- 16. Скачать презентацию













 The category of aspect
The category of aspect Ударение, долгота и краткость. Тема № 2
Ударение, долгота и краткость. Тема № 2 «Взаимодействие с родителями как одно из направлений работы по реализации принципа преемственности между дошкольным образовате
«Взаимодействие с родителями как одно из направлений работы по реализации принципа преемственности между дошкольным образовате Minun kanz (моя семья). Говорим по-вепсски
Minun kanz (моя семья). Говорим по-вепсски Опыт проектирования и строительства автоматизированных парковочных комплексов (АПК)
Опыт проектирования и строительства автоматизированных парковочных комплексов (АПК) Семья – как малая группа
Семья – как малая группа Классный руководитель - авторитет для своих подопечных
Классный руководитель - авторитет для своих подопечных Планирование сбережений - как способ достижения финансовой цели
Планирование сбережений - как способ достижения финансовой цели «Зависли дети в интернете. Мой безопасный Интернет»
«Зависли дети в интернете. Мой безопасный Интернет» Презентація 014
Презентація 014 5 арыс
5 арыс Практическая характерология
Практическая характерология Сжимать иль не сжимать – вот в чем вопрос
Сжимать иль не сжимать – вот в чем вопрос Международный день детской книги
Международный день детской книги Возможности арт-терапии для современного профессионала
Возможности арт-терапии для современного профессионала Любовь в жизни и творчестве Александра Сергеевича Пушкина
Любовь в жизни и творчестве Александра Сергеевича Пушкина Математический КВН между 7 классами.
Математический КВН между 7 классами. ЧТО? ГДЕ? КОГДА?
ЧТО? ГДЕ? КОГДА? Головные и лицевые боли. Анатомия лицевого, тройничного нервов
Головные и лицевые боли. Анатомия лицевого, тройничного нервов Основы переговорного процесса
Основы переговорного процесса Вредные привычки
Вредные привычки Презентация на тему Делимость чисел 6 класс
Презентация на тему Делимость чисел 6 класс Бытовой жанр передвижников
Бытовой жанр передвижников Организация профессиональной педагогической поддержки преподавателя/учителя в современном вузе/школе
Организация профессиональной педагогической поддержки преподавателя/учителя в современном вузе/школе Личный пример родителей по формированию здорового образа жизни (режим дня)
Личный пример родителей по формированию здорового образа жизни (режим дня) МОУ Атемарская средняя общеобразовательная школа - обладатель Гранта Президента Российской Федерации
МОУ Атемарская средняя общеобразовательная школа - обладатель Гранта Президента Российской Федерации Профессии. Швея
Профессии. Швея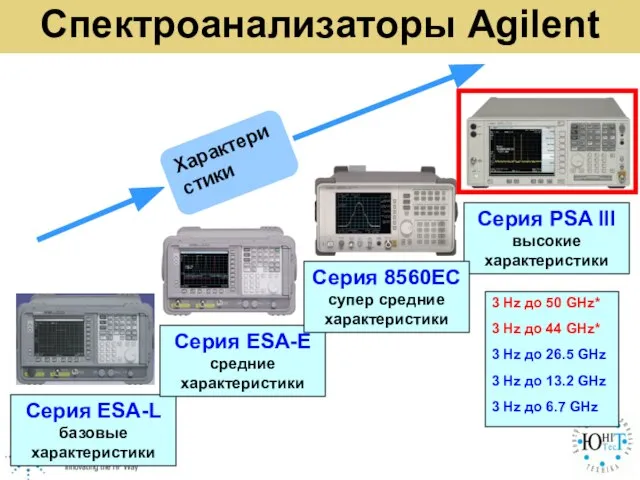 Спектроанализаторы Agilent
Спектроанализаторы Agilent