Содержание
- 2. Формула Пика Задачи на разрезание Сколько узлов на отрезке? Расстояние в «клетчатом» городе Игры на клетчатой
- 3. Задачи на нахождение площади многоугольника. Формула Пика Линии, идущие по сторонам клеток, образуют сетку, а вершины
- 4. Порешаем… Задача 1. В.6 На клетчатой бумаге с клетками размером 1 см × 1 см изображен
- 5. Сколько узлов на отрезке? Теорема. Если р и q взаимно просты, то между А и В
- 6. Порешаем… Задача 1. В прямоугольнике 4×7, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала?
- 7. Задачи на разрезание Классификация задач на разрезание: * Дробление – требуется разрезать данную фигуру: на заданное
- 8. Задача 1. Можно ли разрезать квадрат 6×6 на полоски 1×4 ? Решение. Используем раскраску, показанную на
- 9. Расстояние в «клетчатом» городе Возьмём хорошо знакомый нам листок клетчатой бумаги и представим себе, что это
- 10. Порешаем… Задача 2. Какое наибольшее количество котов можно разместить в узлах сетки на территории квадрата 4×4,
- 11. Игры на клетчатой бумаге Бридж-ит («перебрось мостик!») На рисунке показана доска для игры в бридж-ит. Участники
- 12. Порешаем… Крестики - нолики Популярная игра в крестики – нолики состоит в следующем. Двое по очереди
- 13. Интересные факты Факт 1. Пусть выпуклый многоугольник имеет площадь больше 4 и начало координат является его
- 14. Факт 2. Пусть внутри выпуклой фигуры площади S и периметром 2р лежит узлов решётки. Тогда n
- 15. Список литературы 1. Болотин И. Б., Добрышина Л. Ф. Смоленские математические олимпиады школьников (готовимся к ЕГЭ).
- 17. Скачать презентацию
Слайд 2Формула Пика
Задачи на разрезание
Сколько узлов на отрезке?
Расстояние в «клетчатом» городе
Игры
Формула Пика
Задачи на разрезание
Сколько узлов на отрезке?
Расстояние в «клетчатом» городе
Игры
Интересные факты
Литература
Об авторах
Слайд 3Задачи на нахождение площади многоугольника.
Формула Пика
Линии, идущие по сторонам клеток, образуют
Задачи на нахождение площади многоугольника.
Формула Пика
Линии, идущие по сторонам клеток, образуют
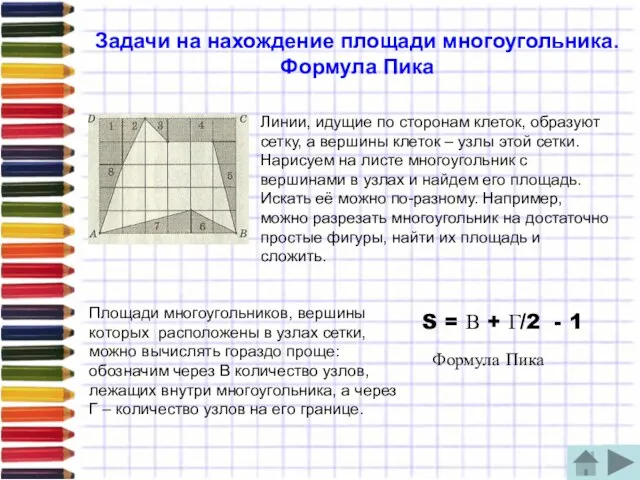
Площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: обозначим через В количество узлов, лежащих внутри многоугольника, а через Г – количество узлов на его границе.
S = В + Г/2 - 1
Формула Пика
Слайд 4Порешаем…
Задача 1. В.6
На клетчатой бумаге с клетками размером 1 см
Порешаем…
Задача 1. В.6
На клетчатой бумаге с клетками размером 1 см
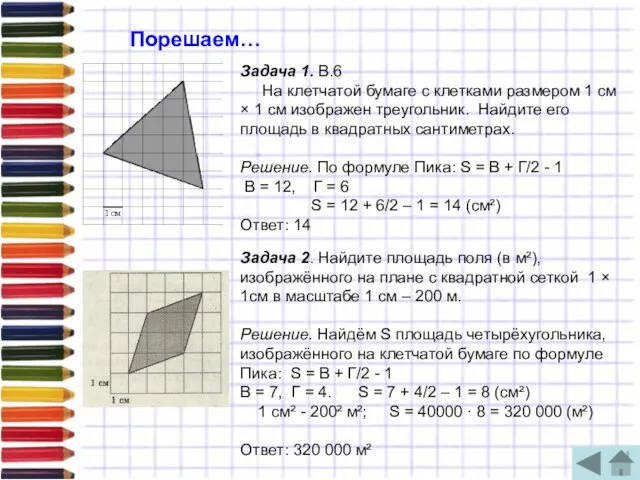
Решение. По формуле Пика: S = В + Г/2 - 1
В = 12, Г = 6
S = 12 + 6/2 – 1 = 14 (см²)
Ответ: 14
Задача 2. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 200 м.
Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + Г/2 - 1
В = 7, Г = 4. S = 7 + 4/2 – 1 = 8 (см²)
1 см² - 200² м²; S = 40000 · 8 = 320 000 (м²)
Ответ: 320 000 м²
Слайд 5Сколько узлов на отрезке?
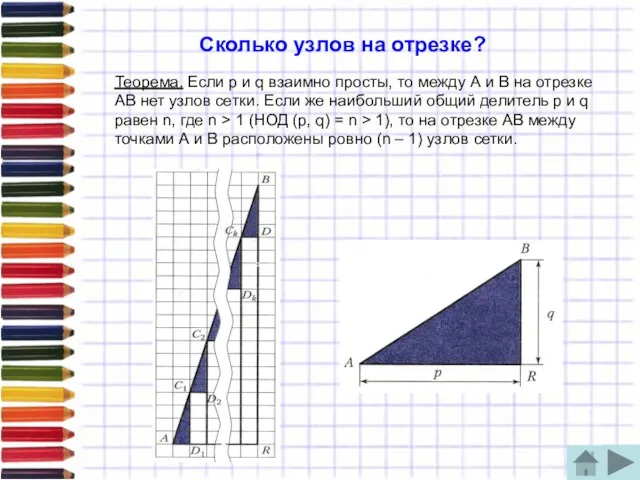
Теорема. Если р и q взаимно просты, то
Сколько узлов на отрезке?
Теорема. Если р и q взаимно просты, то
Слайд 6Порешаем…
Задача 1.
В прямоугольнике 4×7, нарисованном на клетчатой бумаге, провели диагональ. Сколько
Порешаем…
Задача 1.
В прямоугольнике 4×7, нарисованном на клетчатой бумаге, провели диагональ. Сколько

Задачу 1 легко решить, просто «водя пальцем по картинке»
Вдоль диагонали прямоугольника 200×300 можно расположить 100 прямоугольников 2×3, и в каждом из них, очевидно, диагональ будет рассекать по 4 клетки. Поэтому ответ к задаче 2 – четыреста клеток.
Задача 2. В прямоугольнике размером 200×300, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала на две части?
Решение.
Слайд 7Задачи на разрезание
Классификация задач на разрезание:
* Дробление – требуется
Задачи на разрезание
Классификация задач на разрезание:
* Дробление – требуется

на заданное число равных между собой, или, как говорят математики, - конгруэнтных частей (фигур);
на заданное число конгруэнтных и подобных ей фигур (такие фигуры получили название «делящихся»);
определённым количеством прямых на максимально возможное число частей, не обязательно равных.
Возможны и другие вариации условий разрезания, так как фантазия человека не имеет ограничений.
* Квадрирование – разрезание фигуры на возможно меньшее число частей, из которых затем можно сложить квадрат.
* Трансформирование – требуется разрезать одну фигуру так, чтобы их её частей можно было сложить вторую заданную фигуру (не квадрат).
В отдельный подвид можно выделить очень популярные задачи на разрезание шахматной доски, которые отличаются от остальных задач на разрезание тем, что на доске есть раскраска квадратов, и это накладывает дополнительные требования при поиске решения.
Слайд 8 Задача 1. Можно ли разрезать квадрат 6×6 на полоски 1×4 ?
Решение.
Задача 1. Можно ли разрезать квадрат 6×6 на полоски 1×4 ?
Решение.
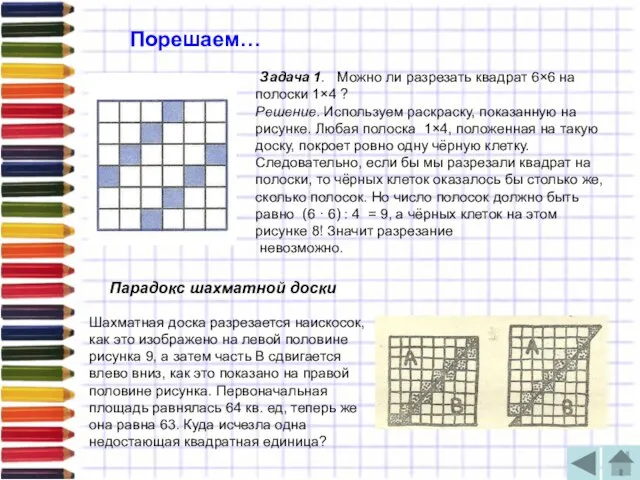
невозможно.
Порешаем…
Парадокс шахматной доски
Шахматная доска разрезается наискосок, как это изображено на левой половине рисунка 9, а затем часть В сдвигается влево вниз, как это показано на правой половине рисунка. Первоначальная площадь равнялась 64 кв. ед, теперь же она равна 63. Куда исчезла одна недостающая квадратная единица?
Слайд 9Расстояние в «клетчатом» городе
Возьмём хорошо знакомый нам листок клетчатой бумаги
Расстояние в «клетчатом» городе
Возьмём хорошо знакомый нам листок клетчатой бумаги

Можно, например, пройти из А в С, а потом – из С в В. Можно было идти через D, а можно – и более замысловатым путём. Что же мы теперь назовём расстоянием от А до В? Конечно, длину кратчайшего пути: 4 + 3 = 7.
А теперь представим себе, что у нас в запасе есть время проделать путь длиной 3. В каких узлах мы можем побывать, выйдя из А? (Или: из каких узлов можно добраться до А, пройдя путь не более 3?)
Ответ на этот вопрос изображён на рисунке
Слайд 10Порешаем…
Задача 2. Какое наибольшее количество котов можно разместить в узлах сетки на
Порешаем…
Задача 2. Какое наибольшее количество котов можно разместить в узлах сетки на

Решение.
Без особого труда мы сумеем поделить территорию квадрата между 13 котами (рис. 1)
Рис. 1
А вот 14 котов мирно ужиться на этой территории уже не смогут. Докажем это. Поделим всю территорию, кроме центра квадрата, на 4 непересекающиеся зоны (рис. 2).
Если даже одного из 14 котов поселить в центре квадрата, то остальных 13 придётся разместить по этим зонам. Значит, в какой-то зоне окажется хотя бы 4 кота.
Перебирая различные варианты расселения 4 котов в какой-нибудь из этих зон, легко увидеть, что это невозможно.
Рис. 2
Слайд 11Игры на клетчатой бумаге
Бридж-ит («перебрось мостик!»)
На рисунке показана
Игры на клетчатой бумаге
Бридж-ит («перебрось мостик!»)
На рисунке показана

Линии противников нигде не должны пересекаться.
Выигрывает тот, кто первым построит ломаную, соединяющую две противоположные стороны доски «своего» цвета.
Так на рисунке выиграли «синие».
В этой игре у начинающего игру есть выигрышная стратегия.
Слайд 12Порешаем…
Крестики - нолики
Популярная игра в крестики – нолики состоит в
Порешаем…
Крестики - нолики
Популярная игра в крестики – нолики состоит в

Выигрывает тот, кто первым поставит определённое количество своих знаков в ряд (по вертикали, горизонтали или диагонали).
Следующая задача относится к этой игре.
Задача
Докажите, что при игре в крестики – нолики второй игрок, как бы хорошо он ни играл, не может рассчитывать больше, чем на ничью, если его партнёр играет правильно.
Слайд 13Интересные факты
Факт 1.
Пусть выпуклый многоугольник имеет площадь больше 4
Интересные факты
Факт 1.
Пусть выпуклый многоугольник имеет площадь больше 4
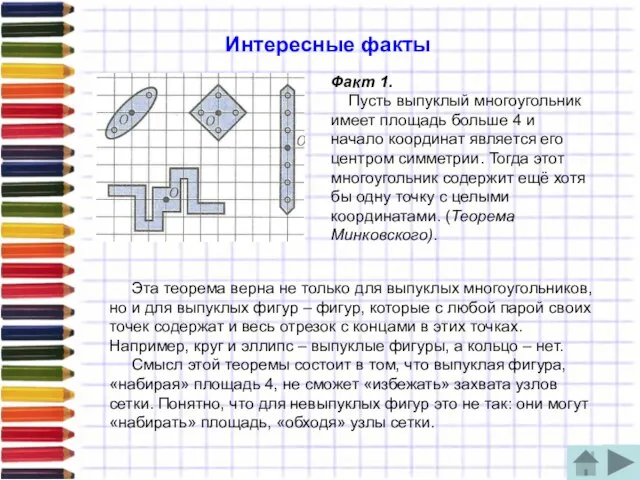
Эта теорема верна не только для выпуклых многоугольников, но и для выпуклых фигур – фигур, которые с любой парой своих точек содержат и весь отрезок с концами в этих точках. Например, круг и эллипс – выпуклые фигуры, а кольцо – нет.
Смысл этой теоремы состоит в том, что выпуклая фигура, «набирая» площадь 4, не сможет «избежать» захвата узлов сетки. Понятно, что для невыпуклых фигур это не так: они могут «набирать» площадь, «обходя» узлы сетки.
Слайд 14 Факт 2. Пусть внутри выпуклой фигуры площади S и периметром 2р
Факт 2. Пусть внутри выпуклой фигуры площади S и периметром 2р

Смысл этого факта таков: если мы захотим оградить на клетчатом листке участок (выпуклый) достаточно большой площади и мы сделаем это, «экономно» расходуя ограду, то на участке окажется довольно много узлов сетки. Если же мы будем расходовать ограду «неэкономно», сильно вытягивая участок, то узлов на участке может оказаться не так много (рис. 1 и 2).
Интересные факты
Величина S – р велика. Площадь мала, а периметр велик.
Узлов много! Узлов нет!
Рис. 1 Рис. 2
Слайд 15Список литературы
1. Болотин И. Б., Добрышина Л. Ф. Смоленские математические олимпиады школьников
Список литературы
1. Болотин И. Б., Добрышина Л. Ф. Смоленские математические олимпиады школьников

2. Геометрия на клетчатой бумаге. Малый МЕХмат МГУ. Режим доступа: http://mmmf.msu.ru/archive/20082009/KanunnikovKuznetsov/2.html
3. Григорьева Г. И. Подготовка школьников к олимпиадам по математике: 5 – 6 классы. Метод. пособие. – М.: Глобус, 2009.
4. Дынкин Е. Б., Молчанов С. А., Розенталь А. Л. Математические соревнования. Арифметика и алгебра. – М.: Наука, 1970.
5. Екимова М. А. ,Кукин Г. П. Задачи на разрезание. М.: МЦНМО, 2002. Режим доступа: http://www.math.ru/lib/files/pdf/kukin.pdf
6. Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.
7. Задачи открытого банка заданий по математике ФИПИ, 2010 – 2011. Режим доступа: http://mathege.ru/or/ege/ShowProblems.html?posMask=32
8. Игнатьев Е. И. В царстве смекалки. – М.: Наука, 1982.
9. Кенгуру – 2010. Задачи, решения, итоги. Режим доступа: http://russian-kenguru.ru/load
10. Прасолов В. В. Задачи по планиметрии. – М.: МЦНМО, 2000.
11. Рисс Е. А. Математический клуб «Кенгуру» Выпуск № 8 (изд. второе). – Санкт-Петербург, 2009.
12. Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.
13. Смирнова И. М., Смирнов В. А. Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010.
14. Смирнов В. А. ЕГЭ. Математика. Задача В6. Планиметрия. Р/т. – М.: МЦНМО, 2011.
15. Трошин В. В. Занимательные дидактические материалы по математике. Сборник заданий. Выпуск 2. – М.: Глобус, 2008.
16. Гарднер М. Математические чудеса и тайны. – М.: Наука, 1986.
 Основные показатели качества приемопередатчиков мобильной связи
Основные показатели качества приемопередатчиков мобильной связи Презентация на тему Природный территориальный комплекс Балтийского моря»
Презентация на тему Природный территориальный комплекс Балтийского моря»  Love birds inspiring company
Love birds inspiring company 28-я Международная специализированная выставка Реклама 2021
28-я Международная специализированная выставка Реклама 2021 Нейтрино. Сохраним вашу энергию
Нейтрино. Сохраним вашу энергию Halloween en France
Halloween en France Управление Кадровым потенциалом(секретное оружие)
Управление Кадровым потенциалом(секретное оружие) ОБЩАЯ ИНФОРМАЦИЯ
ОБЩАЯ ИНФОРМАЦИЯ Семейство розоцветных
Семейство розоцветных Золотая колесница
Золотая колесница Appetite comes with eating
Appetite comes with eating Презентация на тему Перевод целых чисел в 2 8 16-ую систему счисления
Презентация на тему Перевод целых чисел в 2 8 16-ую систему счисления
 Информатика в играх и задачах
Информатика в играх и задачах Презентация
Презентация История отечественной и зарубежной психопатологии
История отечественной и зарубежной психопатологии Презентация на тему Международная торговля товарами и услугами
Презентация на тему Международная торговля товарами и услугами  ОСНОВАНИЯ И СУТЬ ДЕЯТЕЛЬНОСТНОГО ПОДХОДА
ОСНОВАНИЯ И СУТЬ ДЕЯТЕЛЬНОСТНОГО ПОДХОДА МЧС России
МЧС России Невероятные приключения Дмитрия Чулкова: взгляд со стороны
Невероятные приключения Дмитрия Чулкова: взгляд со стороны ОБРАЗОВАНИЕ и сетевое взаимодействие в информационных системахWEB 2.0
ОБРАЗОВАНИЕ и сетевое взаимодействие в информационных системахWEB 2.0 Безопасность игрушек
Безопасность игрушек Контекстная реклама с оплатой за результат
Контекстная реклама с оплатой за результат Программа УМНИК. Стимулирование участия молодежи в научно-технической деятельности путем организационной и финансовой поддержки
Программа УМНИК. Стимулирование участия молодежи в научно-технической деятельности путем организационной и финансовой поддержки Франция. Долгий путь к единству
Франция. Долгий путь к единству Технология пайки печатных плат с использованием ИК-нагрева
Технология пайки печатных плат с использованием ИК-нагрева Понятие и сущность права. (Тема 5)
Понятие и сущность права. (Тема 5) Савельева О.И.Генеральный директор ИНСТИТУТА ЭКОНОМИКИ ЖИЛИЩНО-КОММУНАЛЬНОГО ХОЗЯЙСТВА
Савельева О.И.Генеральный директор ИНСТИТУТА ЭКОНОМИКИ ЖИЛИЩНО-КОММУНАЛЬНОГО ХОЗЯЙСТВА Все профессии важны
Все профессии важны