Задачи на переливание

Содержание:
1. Введение
1.1 Цель исследования;
1.2 Задачи исследования;
2. Типичные задачи на переливания;
3. Задача Пуассона;
4. Методы решения задач на переливания
4.1 Метод рассуждений;
4.2 Метод таблиц;
4.3 Метод математического бильярда;
5. Условие разрешимости задач;
6. Вывод;
7. Список литературы;
8. Приложение.

Цель исследования:
Рассмотреть различные способы решения алгебраических задач на переливание жидкости.

Достижение указанной цели предполагает решение следующих задач:
выявить, какие существуют способы решения задач на переливание;
рассмотреть возможность применения геометрии, а именно способ математического бильярда, к решению подобных задач.

Задачи на переливание
Задачи на концентрацию
Задачи непосредственно на переливание жидкости из одного сосуда в другой

В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи.
Если не сказано ничего другого, считается, что
Все сосуды без делений;
Нельзя переливать жидкости «на глаз».

Задача Пуассона
Самая древняя из задач на переливание – задача Пуассона.
Знаменитый французский математик, механик и физик Симеон Дени Пуассон (1781 – 1840) решил эту задачу в юности и впоследствии говорил, что именно она побудила его стать математиком.

Условие задачи
Один человек имеет в бочонке 12 пинт вина (пинта – старинная французская мера объема, 1 пинта ≈ 0,568 л) и хочет подарить половину вина, но у него нет сосуда в 6 пинт, однако имеются два пустых сосуда объемом 8 пинт и 5 пинт. Как с их помощью отлить ровно 6 пинт вина?

Методы решения логических задач на переливание:
Метод рассуждений;
Метод таблиц;
Метод блок-схем;
Метод бильярда;
Метод трилинейных координат

Метод рассуждений:
Идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.

Метод таблиц
Идея метода заключается в построении таблиц, которые не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

0 П
0 П

0 П

3 П
5 П

3 П

6 П

6 П
0 П

Решение:
Сначала наливаете 8 литров в 8-литровый, потом из 8-литрового наливаете полный 5-литровый, в результате получается, что в 12-литровом - 4 литра, в 8-литровом – 3 литра, а в 5-литровом – 5 литров.
Переливаете из 5-литрового в 12-литровый всю воду (или что там за жидкость), а из 8-литрового переливаете все 3 литра в 5-литровый. В результате 9 литров в 12-литровом, 0 литров в 8-литровом, и 3 литра в 5-литровом. Переливаете из 12-литрового 8 литров в пустой 8-литровый, и в 12-литровом остается 1 литр. Из 8-литрового доливаете в 5-литровый, пока 5-литровый не станет полным, (в 5-литровом было 3 литра, следовательно долили мы еще 2 литра из 8-литрового) Тогда в 8-литровом как раз остается 6 литров.

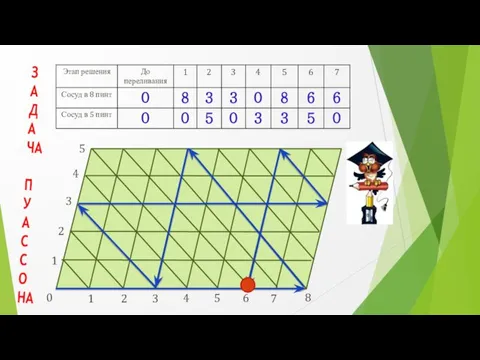
Метод математического бильярда

Суть метода заключается в представлении последовательности переливаний аналогично движению бильярдного шарика по столу особой конструкции с размерами, соответствующими объемам первоначально пустых сосудов. Нарисовав на клетчатой бумаге исходную конфигурацию, необходимо проследить возможные движения шарика в соответствии с законом «угол падения равен углу отражения» и попадание им в требуемые точки по условию задачи.

1
1
2
4
7
6
5
8
3
4
3
2
5
0
З
А
Д
А
ЧА
П
У
А
С
С
О
НА

Вывод:
Нами были рассмотрены методы решения алгебраических задач на переливание с помощью рассуждений, таблиц и математического бильярда.
Рассматриваемые методы можно использовать и при решение различных практических задач на переливание жидкостей.

Я отпил ¼ чашечки кофе и долил её молоком.
Потом выпил ½ чашечки и снова долил её доверху молоком. Потом я выпил четверть чашечки и опять долил её молоком.
… И тогда я выпил полную чашечку целиком…Чего я выпил больше – кофе или молока?

Решение:
Надо посчитать в долях кофейной чашечки, сколько же я доливал в неё молока:
1/4 +1/2+1/4=1
Получается целая чашечка молока. Следовательно, я выпил чашечку кофе и столько же молока.
https://vk.com/club52786470

Школьник - это не сосуд, который надо заполнить знаниями, а факел, который нужно зажечь.
Л.А. Арцимович