Задачи по моделированию в среде Excel”

Компьютерный эксперимент
Чтобы дать жизнь новым конструкторским разработкам, внедрить новые технические решения в производство или проверить новые идеи, нужен эксперимент. В недалеком прошлом такой эксперимент можно было провести либо в лабораторных условиях на специально создаваемых для него установках, либо на натуре, т.е. на настоящем образце изделия, подвергая его всяческим испытаниям. Это требует больших материальных затрат и времени. В помощь пришли компьютерные исследования моделей. При проведении компьютерного эксперимента проверяют правильность построения моделей. Изучают поведение модели при различных параметрах объекта. Каждый эксперимент сопровождается осмыслением результатов. Если результаты компьютерного эксперимента противоречат смыслу решаемой задачи, то ошибку надо искать в неправильно выбранной модели или в алгоритме и методе ее решения. После выявления и устранения ошибок компьютерный эксперимент повторяется.

Под математической моделью понимают систему математических соотношений — формул, уравнений неравенств и т.д., отражающих существенные свойства объекта или процесса.

Задачи по моделированию из различных предметных областей
Экономика
Астрономия
Физика
Экология
Биология
География

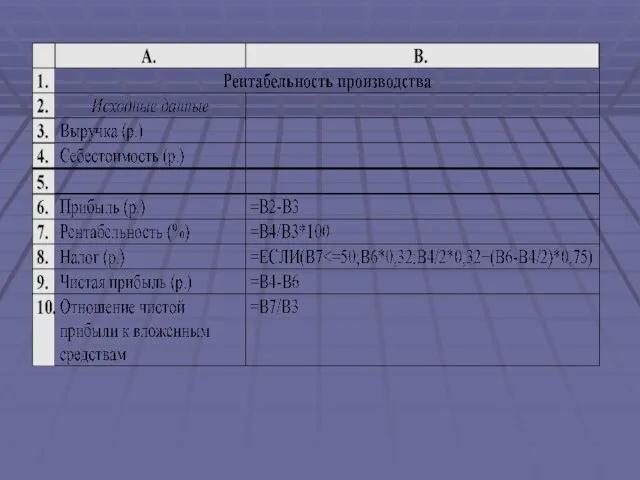
Машиностроительный завод, реализуя продукцию по договорным ценам, получил определенную выручку, затратив на производство некоторую сумму денег. Определить отношение чистой прибыли к вложенным средствам.
Постановка задачи
Цель моделирования — исследовать процесс производства и реализации продукции с целью получения наибольшей чистой прибыли. Пользуясь экономическими формулами найти отношение чистой прибыли к вложенным средствам.
Экономика

Основными параметрами объекта моделирования являются: выручка, себестоимость, прибыль, рентабельность, налог с прибыли.
Исходные данные:
выручка B;
затраты (себестоимость) S.
Другие параметры найдем, используя основные экономические зависимости. Значение прибыли определяется как разность между выручкой и себестоимостью P=B-S.
Рентабельность r вычисляется по формуле: .
Прибыль, соответствующая предельному уровню рентабельности 50%, составляет 50% от себестоимости продукции S, т.е. S*50/100=S/2, поэтому налог с прибыли N определяется следующим образом:
если r<=50, то N=P*32/100 р., иначе N=S/2*32/100+(P-S/2)*75/100.
Чистая прибыль Рч=Р-N.
И, наконец, результат решения этой задачи — отношение чистой прибыли к вложенным средствам q= Рч/S.
Так выглядит электронная таблица в формате отображения формул:

Анализ результатов
Полученная модель позволяет в зависимости от рентабельности определять налог с прибыли, автоматически пересчитывать размер чистой прибыли, находить отношение чистой прибыли к вложенным средствам.
Проведенный компьютерный эксперимент показывает, что отношение чистой прибыли к вложенным средствам увеличивается при увеличении выручки и уменьшается при увеличении себестоимости продукции.

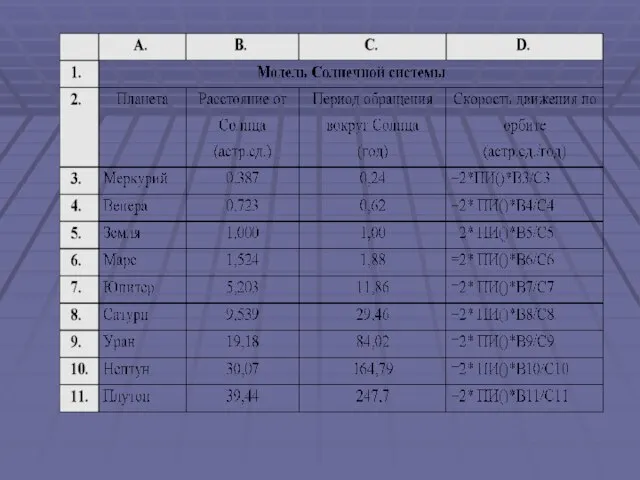
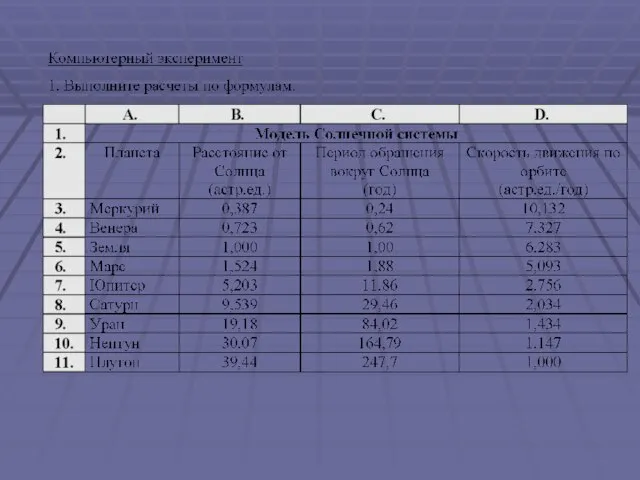
Задача .
Определите скорость движения планет по орбите. Для этого составьте компьютерную модель Солнечной системы.
Постановка задачи
Цель моделирования — определить скорость движения планет по орбите.
Объект моделирования — Солнечная система, элементами которой являются планеты. Внутреннее строение планет в расчет не принимается. Будем рассматривать планеты как элементы, обладающие следующими характеристиками:
название;
R - удаленность от Солнца (в астрономических единицах;
астроном. ед. — среднее расстояние от Земли до Солнца);
t - период обращения вокруг Солнца (в годах);
V - скорость движения по орбите (астр.ед./год), предполагая, что планеты
движутся вокруг Солнца по окружностям с постоянной скоростью.
Астрономия

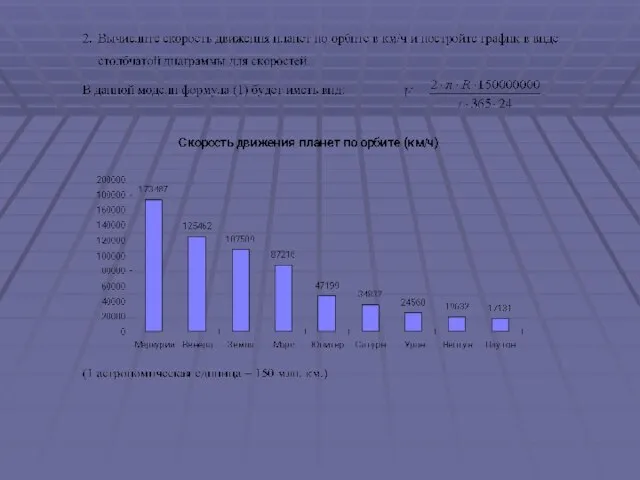
Анализ результатов
1. Проанализируйте результаты расчетов. Можно ли утверждать, что планеты, находящиеся ближе к Солнцу имеют большую скорость движения по орбите?
2. Представленная модель Солнечной системы является статической. При построении этой модели мы пренебрегали изменениями расстояния от планет до Солнца во время их движения по орбите. Чтобы знать, какая планета дальше и каковы примерные соотношения между расстояниями, этой информации вполне достаточно. Если же мы хотим определить расстояние между Землей и Марсом, то пренебрегать временными изменениями нельзя, и здесь придется использовать уже динамическую модель.

Физика

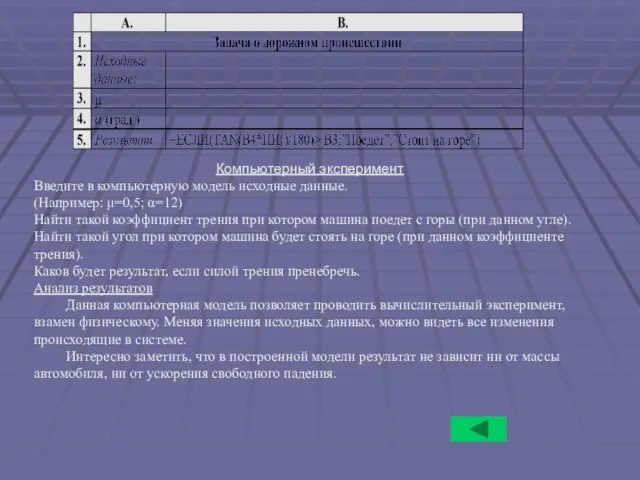
Компьютерный эксперимент
Введите в компьютерную модель исходные данные.
(Например: μ=0,5; α=12)
Найти такой коэффициент трения при котором машина поедет с горы (при данном угле).
Найти такой угол при котором машина будет стоять на горе (при данном коэффициенте трения).
Каков будет результат, если силой трения пренебречь.
Анализ результатов
Данная компьютерная модель позволяет проводить вычислительный эксперимент, взамен физическому. Меняя значения исходных данных, можно видеть все изменения происходящие в системе.
Интересно заметить, что в построенной модели результат не зависит ни от массы автомобиля, ни от ускорения свободного падения.

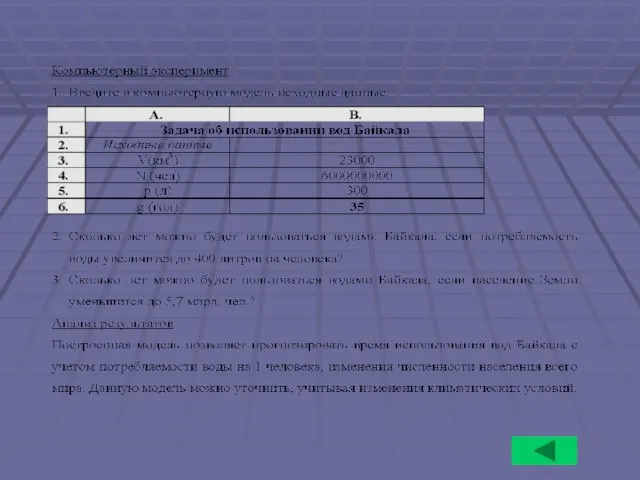
Задача .
Представьте себе, что на Земле останется только один источник пресной воды — озеро Байкал. На сколько лет Байкал обеспечит население всего мира водой?
Экология

Разработка модели
Для построения математической модели определим исходные данные. Обозначим:
V - объем озера Байкал 23000 км3;
N - население Земли 6 млрд. чел.;
p - потребление воды в день на 1 человека (в среднем) 300 л.
Так как 1л. = 1 дм3 воды, необходимо выполнить перевод V воды озера из км3 в дм3. V (км3) = V * 109 (м3) = V * 1012 (дм3)
Результат — количество лет, за которое население Земли использует воды Байкала, обозначим g. Итак, g=(V*1000000000000)/(N*p*365)
Так выглядит электронная таблица в режиме отображения формул:

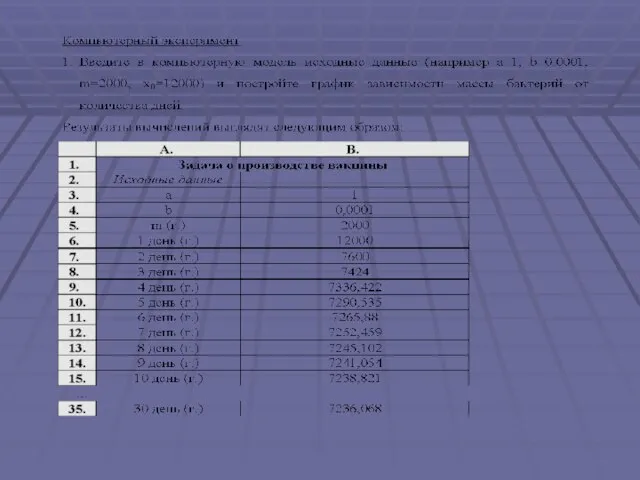
Задача .
Для производства вакцины на заводе планируется выращивать культуру бактерий. Известно, что если масса бактерий - x г., то через день она увеличится на (a-bx)x г., где коэффициенты a и b зависят от вида бактерий. Завод ежедневно будет забирать для нужд производства вакцины m г. бактерий. Для составления плана важно знать, как изменяется масса бактерий через 1, 2, 3, ..., 30 дней..
Биология

Задача .
Какова будет численность населения России в 2010 году?
География

Постановка задачи
Объектом моделирования является процесс изменения численности населения в зависимости от времени. На этот процесс влияют многие факторы: экология, состояние медицинского обслуживания, экономическая ситуация в стране, международная обстановка и многое другое. Обобщив демографические данные, ученые вывели функцию, выражающую зависимость численности населения от времени:
f(t)=где коэффициента a и b для каждого государства свои,
e основание натурального логарифма.
Эта формула лишь приближенно отражает реальность. Для нахождения значений коэффициентов a и b можно воспользоваться статистическим справочником. Взяв из справочника значения f(t) (численность населения в момент времени t), можно приближенно подобрать a и b так, чтобы теоретические значения f(t), вычисляемые по формуле, не сильно отличались от фактических данных в справочнике.