Содержание
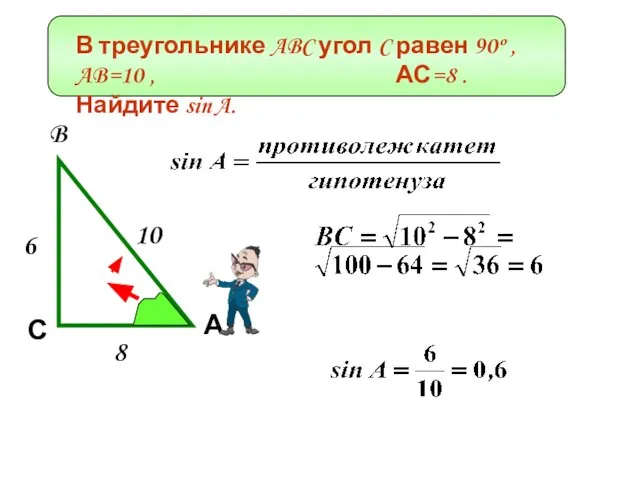
- 2. В треугольнике ABC угол C равен 90º , AB=10 , АС=8 . Найдите sin A. С
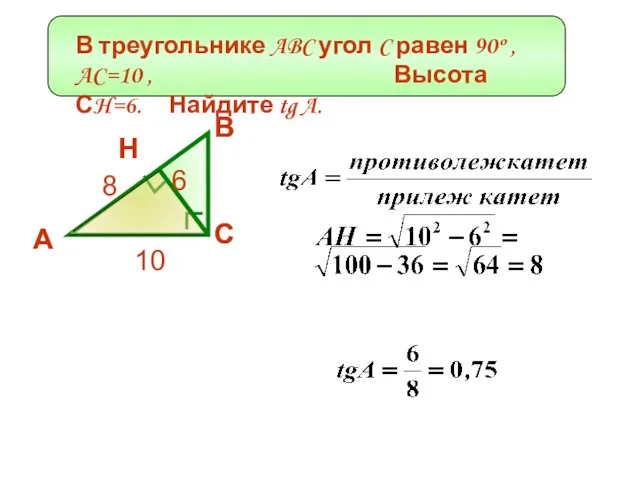
- 3. В треугольнике ABC угол C равен 90º , AC=10 , Высота СH=6. Найдите tg A. Н
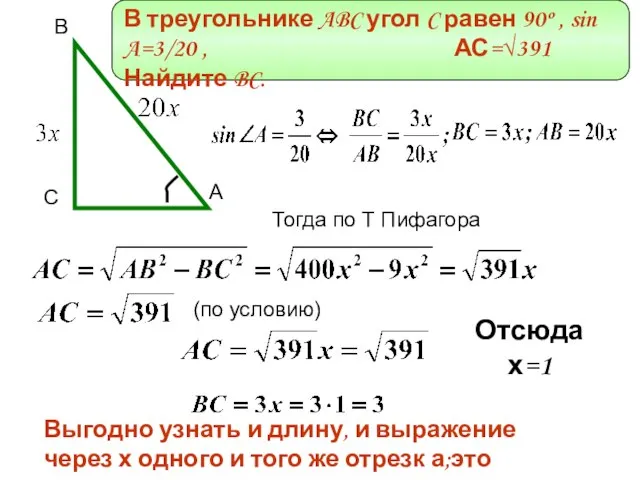
- 4. В треугольнике ABC угол C равен 90º , sin A=3/20 , АС=√391 Найдите BC. С В
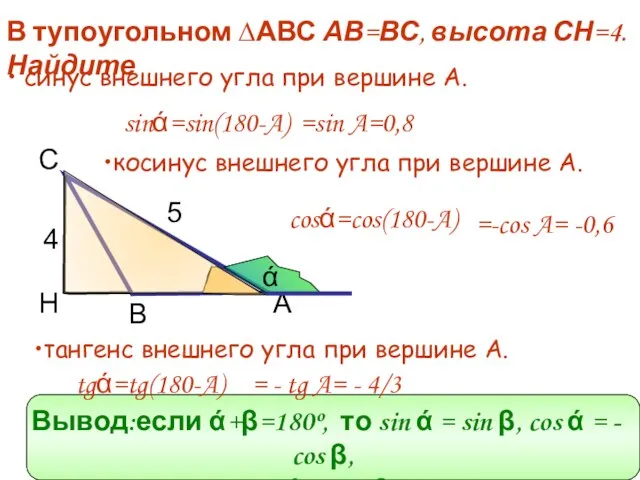
- 5. С 5 4 А Н В В тупоугольном ∆АВС АВ=ВС, высота СН=4. Найдите косинус внешнего угла
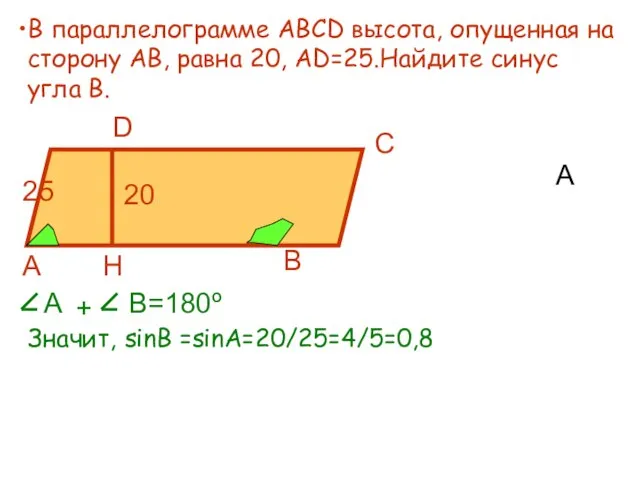
- 6. А В параллелограмме АВСD высота, опущенная на сторону АВ, равна 20, АD=25.Найдите синус угла В. Значит,
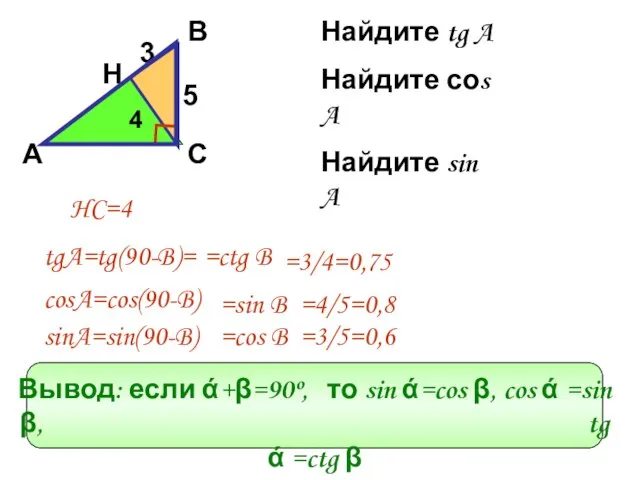
- 7. Найдите tg A Найдите соs A Найдите sin A tgA=tg(90-B)= =ctg B cosA=cos(90-B) =sin B sinA=sin(90-B)
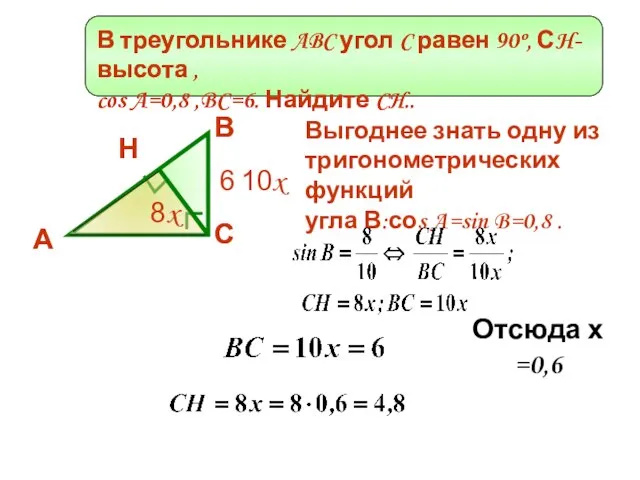
- 8. В треугольнике ABC угол C равен 90º, СH-высота , cos A=0,8 ,BC=6. Найдите CH.. Н С
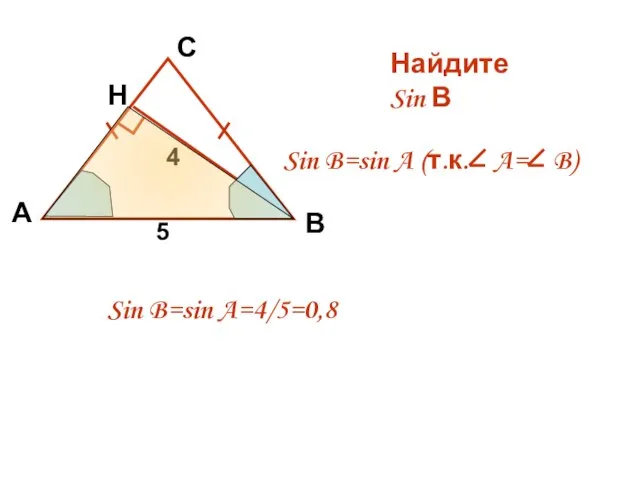
- 9. А С Н 4 5 Найдите Sin В В Sin B=sin A (т.к. A= B) Sin
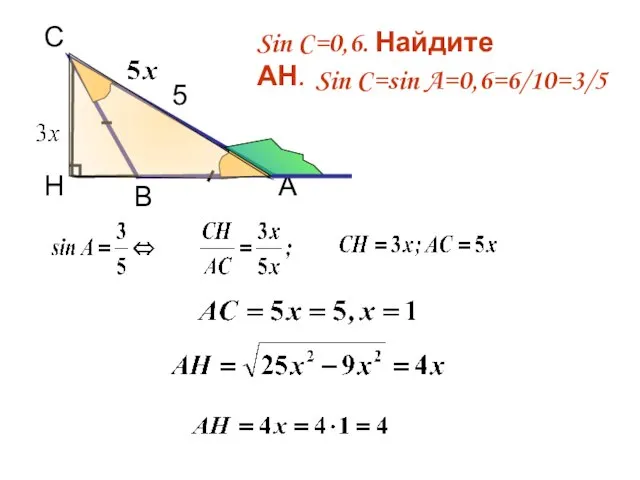
- 10. С 5 А Н В Sin C=0,6. Найдите АН. Sin C=sin A=0,6=6/10=3/5
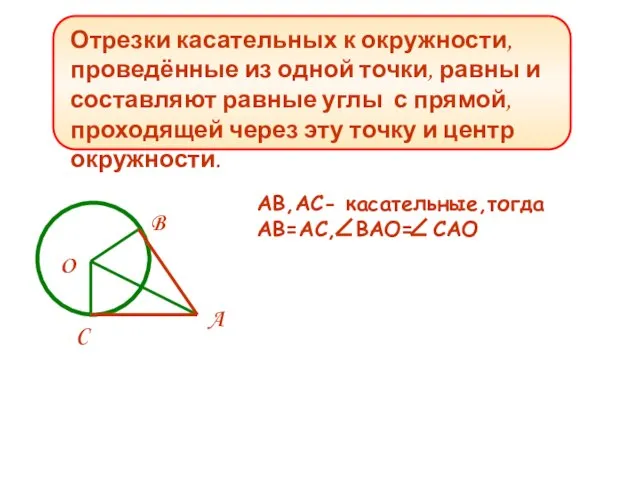
- 11. Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей
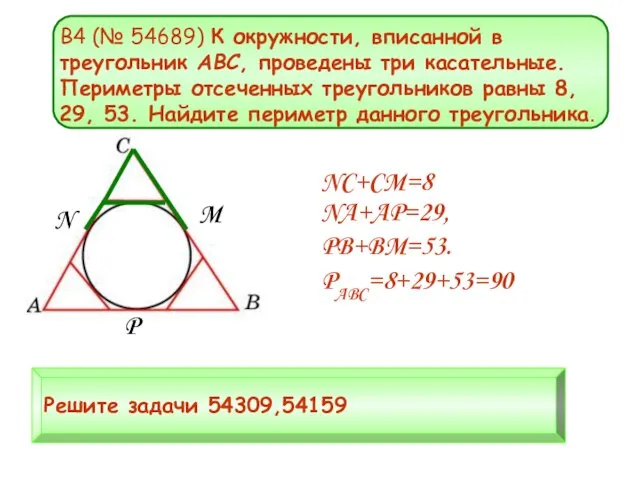
- 12. B4 (№ 54689) К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны
- 13. B4 (№ 54309) Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон
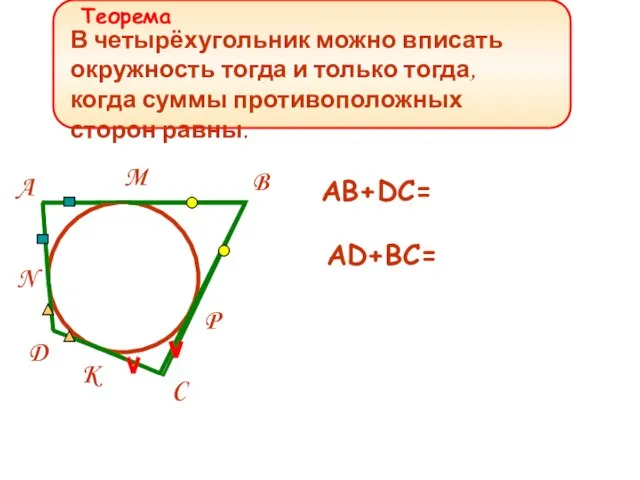
- 14. В четырёхугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны. P K
- 15. B4 (№ 54599) В четырехугольник ABCD вписана окружность, АВ=6, ВС=2, СД=14. Найдите четвёртую сторону. A B
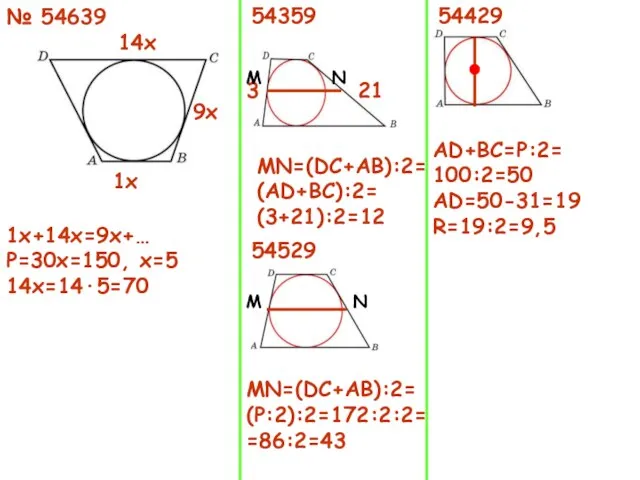
- 16. № 54639 1х+14х=9х+… Р=30х=150, х=5 14х=14·5=70 54359 1х 9х 14х 21 3 МN=(DC+AB):2= (AD+BC):2= (3+21):2=12 54529
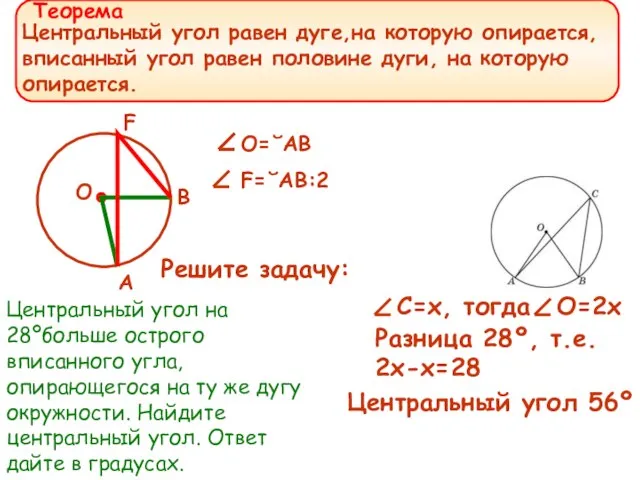
- 17. Центральный угол равен дуге,на которую опирается, вписанный угол равен половине дуги, на которую опирается. O=˘AB F=˘AB:2
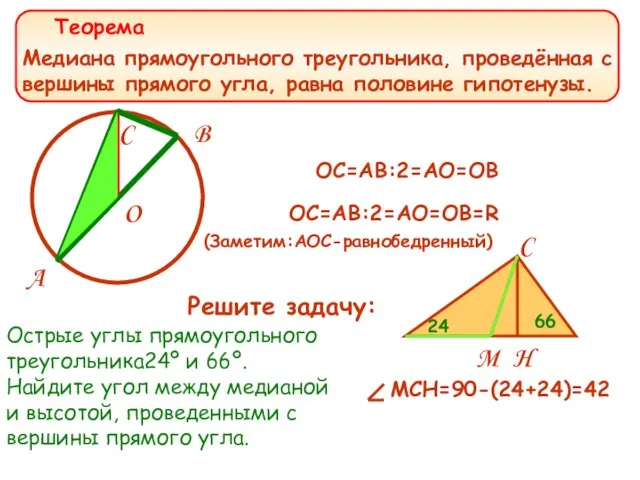
- 18. Медиана прямоугольного треугольника, проведённая с вершины прямого угла, равна половине гипотенузы. OC=AB:2=AO=OB O C B A
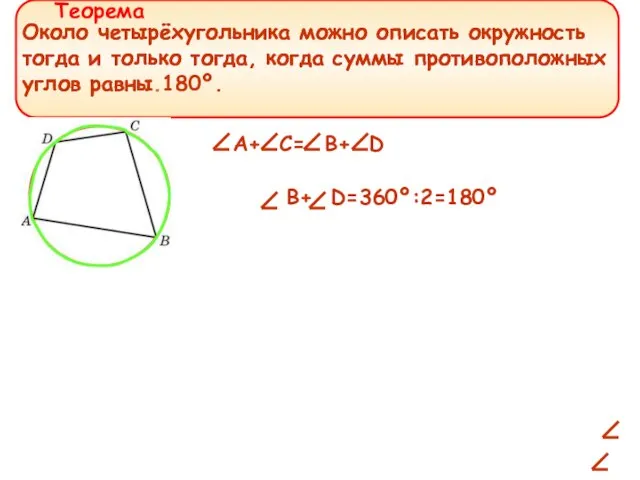
- 19. Около четырёхугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны. Около четырёхугольника
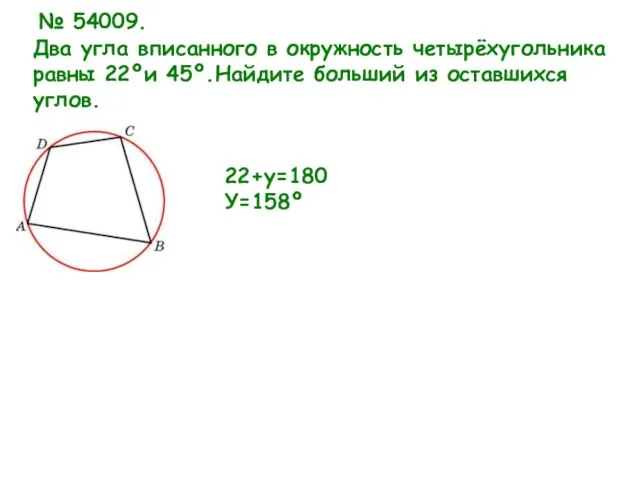
- 20. Два угла вписанного в окружность четырёхугольника равны 22ºи 45º.Найдите больший из оставшихся углов. № 54009. 22+у=180
- 22. Скачать презентацию


 Презентация на тему Гидросфера
Презентация на тему Гидросфера БАНКИЗАЦИЯ РОССИИ И ЭКОНОМИЧЕСКИЙ РОСТ
БАНКИЗАЦИЯ РОССИИ И ЭКОНОМИЧЕСКИЙ РОСТ Марксистко-ленинская парадигма
Марксистко-ленинская парадигма Спутники планет
Спутники планет Иллюстрации к стихам Агнии Львовны Барто
Иллюстрации к стихам Агнии Львовны Барто Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Сложение и вычитание многочленов
Сложение и вычитание многочленов Lektsia_3_1_opredelenie_prochnosti_kirpicha_i_metalla_ispytania_Avtosokhranennyi_774
Lektsia_3_1_opredelenie_prochnosti_kirpicha_i_metalla_ispytania_Avtosokhranennyi_774 Тротуары по улице Первомайская
Тротуары по улице Первомайская Мы приглашаем вас в музей
Мы приглашаем вас в музей Основные направления культуры России первой половины XIX века
Основные направления культуры России первой половины XIX века Гендерная программа Всемирного банка в России
Гендерная программа Всемирного банка в России Г. Остер
Г. Остер М.А.Шолохов. Жизнь,творчество, личность
М.А.Шолохов. Жизнь,творчество, личность Алгоритм деятельности общеобразовательного учреждения в условиях введения новых образовательных стандартов основного общего об
Алгоритм деятельности общеобразовательного учреждения в условиях введения новых образовательных стандартов основного общего об Анри Картье-Брессон. Уличная фотография
Анри Картье-Брессон. Уличная фотография Консультации и Вебинары по личностному росту и Отношениям
Консультации и Вебинары по личностному росту и Отношениям Подготовка волонтерского корпуса для международного чемпионата в сфере строительства World Construction Championship
Подготовка волонтерского корпуса для международного чемпионата в сфере строительства World Construction Championship Тест по технологии 5 Класс Раздел программы: «Материаловедение»
Тест по технологии 5 Класс Раздел программы: «Материаловедение» Rice Moti. Наша ниша на рынке
Rice Moti. Наша ниша на рынке Связь справедливости взаимодействия с эмоциями участников (на примере политических выборов)
Связь справедливости взаимодействия с эмоциями участников (на примере политических выборов) Присвоение имен диапазонам
Присвоение имен диапазонам  Пути к бесконфликтной дисциплине
Пути к бесконфликтной дисциплине Презентация на тему Первые русские князья
Презентация на тему Первые русские князья  Наркомания
Наркомания Философия науки
Философия науки Обзор технологии доступа к данным
Обзор технологии доступа к данным  Основные литературные направления
Основные литературные направления