Содержание
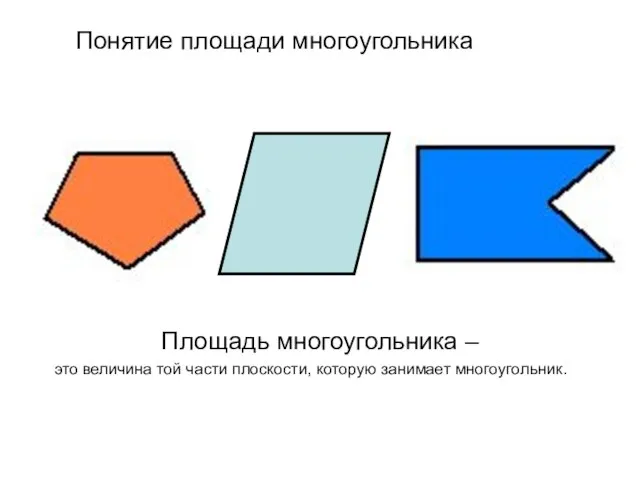
- 2. Понятие площади многоугольника Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
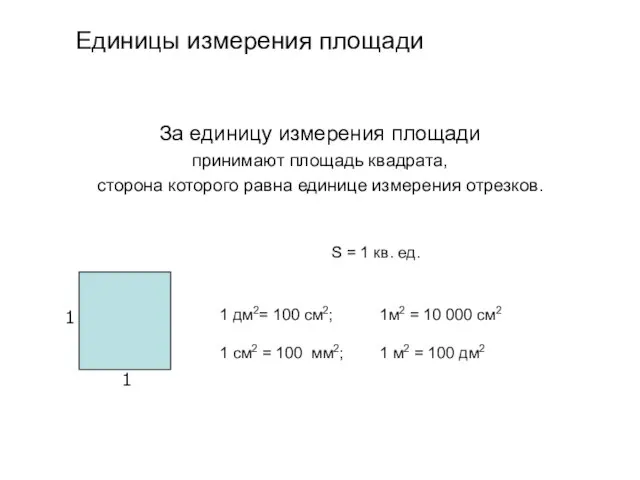
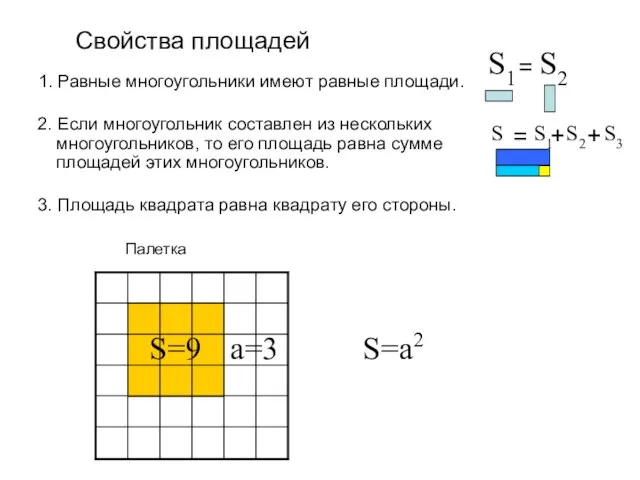
- 3. За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков. 1 1 Единицы
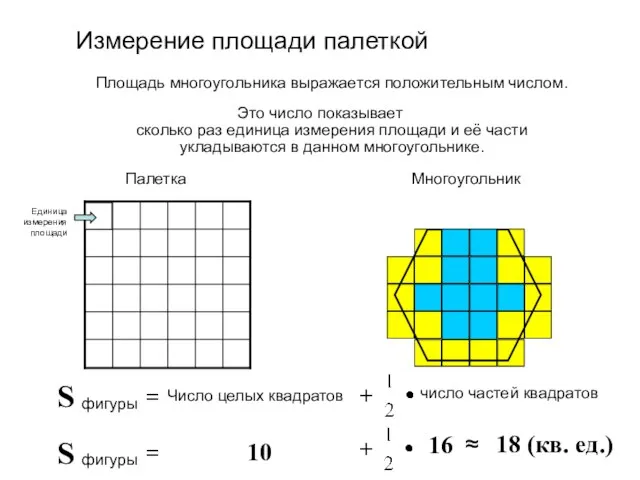
- 4. Это число показывает сколько раз единица измерения площади и её части укладываются в данном многоугольнике. Палетка
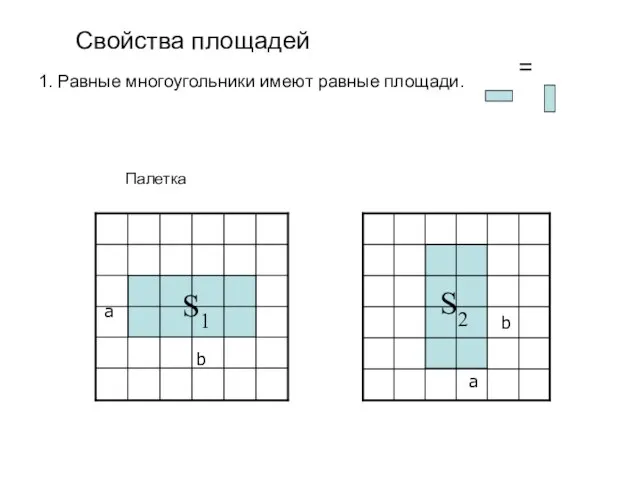
- 5. a b 1. Равные многоугольники имеют равные площади. a b Свойства площадей Палетка S1 S2 =
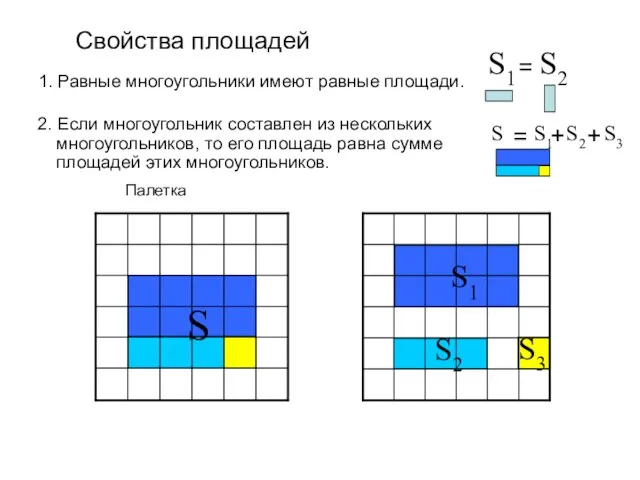
- 6. 1. Равные многоугольники имеют равные площади. Свойства площадей Палетка S1 S2 = 2. Если многоугольник составлен
- 7. 1. Равные многоугольники имеют равные площади. Свойства площадей Палетка S1 S2 = 2. Если многоугольник составлен
- 8. №1. На продолжении стороны DC параллелограмма ABCD за точку C отмечена точка M так, что DC=CM.
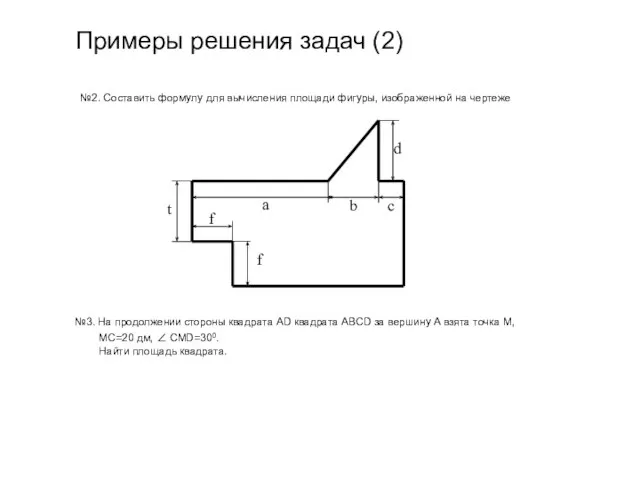
- 9. Примеры решения задач (2) №2. Составить формулу для вычисления площади фигуры, изображенной на чертеже №3. На
- 10. Площадь прямоугольника Площадь прямоугольника равна произведению его смежных сторон. b Дано: a, b – стороны прямоугольника
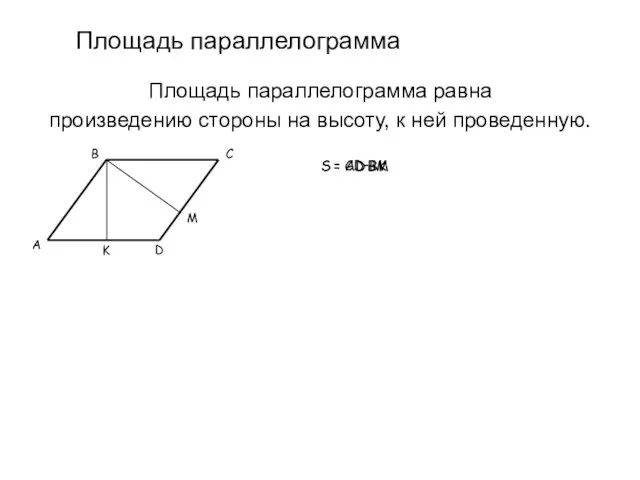
- 11. Площадь параллелограмма Площадь параллелограмма равна произведению стороны на высоту, к ней проведенную. B D C A
- 12. Площадь параллелограмма Площадь параллелограмма равна произведению стороны на высоту, к ней проведенную. B D C A
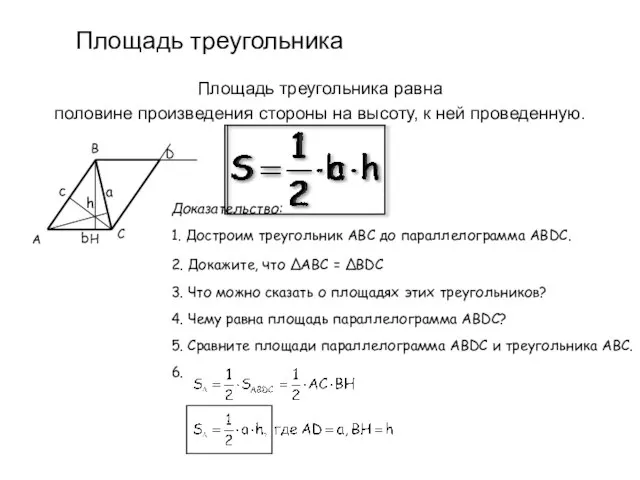
- 13. Площадь треугольника Площадь треугольника равна половине произведения стороны на высоту, к ней проведенную. B C D
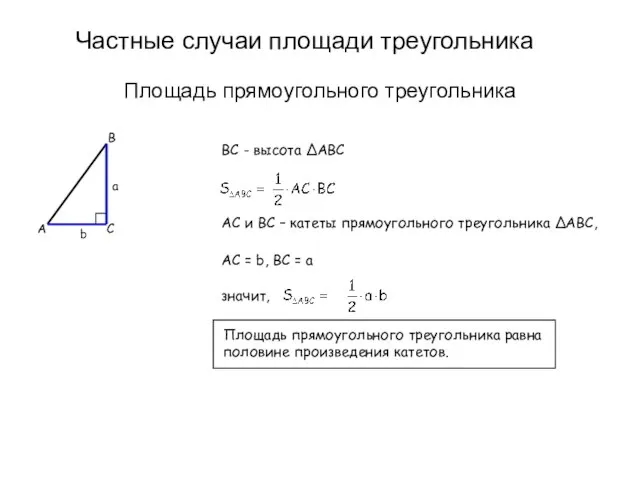
- 14. Частные случаи площади треугольника Площадь прямоугольного треугольника B C A b a BC - высота ΔABC
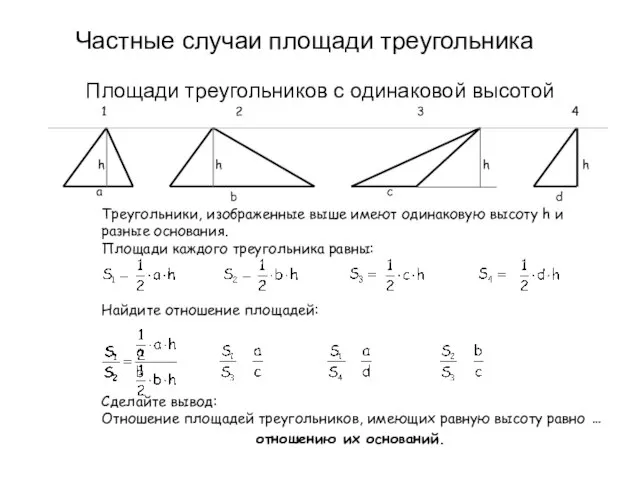
- 15. Частные случаи площади треугольника Площади треугольников с одинаковой высотой a Сделайте вывод: Отношение площадей треугольников, имеющих
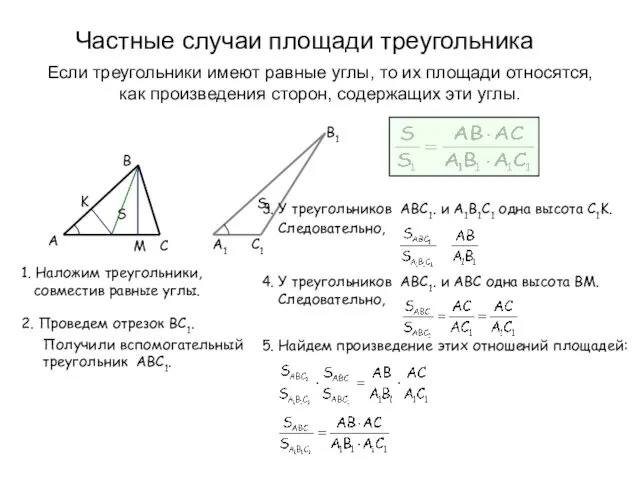
- 16. S1 Частные случаи площади треугольника Если треугольники имеют равные углы, то их площади относятся, как произведения
- 18. Скачать презентацию



 Говорим по-английски.
Говорим по-английски. Презентация : «Человек-феномен» Выполнила: Ученица 9 класса Озерова Дарья Руководитель: Учитель обществознания Самуйленко Т.В.
Презентация : «Человек-феномен» Выполнила: Ученица 9 класса Озерова Дарья Руководитель: Учитель обществознания Самуйленко Т.В. К А М П А Н И Я
К А М П А Н И Я Почему планеты разных размеров?
Почему планеты разных размеров? Помоги мышонку и пройди лабиринт
Помоги мышонку и пройди лабиринт Геофизические методы поисков и разведки месторождений полезных ископаемых
Геофизические методы поисков и разведки месторождений полезных ископаемых Алгоритм работы с текстом
Алгоритм работы с текстом Сущность налогов
Сущность налогов Полимерная глина
Полимерная глина «Обломов» — роман-предупреждение
«Обломов» — роман-предупреждение Свойства и состояния воды
Свойства и состояния воды НЕБЛАГОПРИЯТНЫЕ ЛЕКАРСТВЕННЫЕ РЕАКЦИИ
НЕБЛАГОПРИЯТНЫЕ ЛЕКАРСТВЕННЫЕ РЕАКЦИИ Применение солнечной энергетики в городском хозяйстве Москвы
Применение солнечной энергетики в городском хозяйстве Москвы Продукт ActivaScrewTM Канюлированный биодеградируемый винт
Продукт ActivaScrewTM Канюлированный биодеградируемый винт “Обсуждение техники, стратегии и целей присоединения к ВТО: что следует делать Беларуси?” “Анализ практики разрешения споров по
“Обсуждение техники, стратегии и целей присоединения к ВТО: что следует делать Беларуси?” “Анализ практики разрешения споров по Культура Индии
Культура Индии Формирование информационной культуры
Формирование информационной культуры Цивильск
Цивильск Путешествие в сказку
Путешествие в сказку Танк Т-26
Танк Т-26 Топ-5 самых дорогих сортов кофе
Топ-5 самых дорогих сортов кофе Мой Консультант Плюс
Мой Консультант Плюс Муниципальное бюджетное дошкольное образовательное учреждение детский сад № 24
Муниципальное бюджетное дошкольное образовательное учреждение детский сад № 24 Гибкая подводка
Гибкая подводка Виртуальный лабораторный практикум по физике
Виртуальный лабораторный практикум по физике Товарная политика
Товарная политика Презентация на тему Политическая жизнь общества
Презентация на тему Политическая жизнь общества Основы государства и права. Монархия и демократия
Основы государства и права. Монархия и демократия