Содержание
- 2. МЕТОДЫ РАСЧЕТА РАЗМЕРНЫХ ЦЕПЕЙ Сущность расчета размерной цепи заключается в установлении номинальных размеров, допусков и предельных
- 3. Точность сборки обеспечивается на основе расчета размерных цепей. Метод полной взаимозаменяемости — это метод, при котором
- 4. При анализе размерных цепей обычно решают два класса задач: Обратная задача - задача, в которой известны
- 13. Метод неполной взаимозаменяемости исходит из предложения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный
- 14. Закон равной вероятности Закон треугольника
- 15. λ - коэффициент относительного рассеяния, зависит от закона распределения размера. Координата середины поля допуска замыкающего звена,
- 16. Уравнение номинальных размеров цепи: АΔ=А1-А2-А3=190-150-40=0 мм Проверяем возможность обеспечения точности замыкающего звена по методу полной взаимозаменяемости:
- 18. Прямая (проектная) задача расчета размерных цепей Рассчитать допуски на размеры составляющих звеньев при заданной точности сборки,
- 20. 4 задание Расчет размерных цепей 1. Рассчитать заданную размерную цепь по методу полной взаимозаменяемости (max-min), решить
- 22. Скачать презентацию
Слайд 2МЕТОДЫ РАСЧЕТА РАЗМЕРНЫХ ЦЕПЕЙ
Сущность расчета размерной цепи заключается в установлении номинальных размеров,
МЕТОДЫ РАСЧЕТА РАЗМЕРНЫХ ЦЕПЕЙ
Сущность расчета размерной цепи заключается в установлении номинальных размеров,

1) определение допусков и предельных отклонений размеров составляющих звеньев по заданным номинальным размерам всех размеров цепи и заданным предельным размерам исходного звена (прямая задача, проектный расчет);
2) определение номинального размера, предельных отклонений и допуска замыкающего звена по заданным номинальным размерам и предельным отклонениям составляющих звеньев (обратная задача, проверочный расчет).
Применяются следующие методы обеспечения точности при сборке :
— полной взаимозаменяемости;
— неполной взаимозаменяемости;
— пригонки;
— регулирования;
— групповой взаимозаменяемости.
Слайд 3Точность сборки обеспечивается на основе расчета размерных цепей.
Метод полной взаимозаменяемости — это
Точность сборки обеспечивается на основе расчета размерных цепей.
Метод полной взаимозаменяемости — это

При этом методе используется способ расчета на максимум-минимум.
Способ максимума-минимума предполагает, что в процессе сборки узла или обработки детали возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих размеров или обратное их сочетание. Однако практически такое сочетание маловероятно, так как отклонение размеров в основном группируется около середины поля допуска.
Метод неполной взаимозаменяемости допускает приемлемый процент изделий, у которых замыкающее звено выйдет за поле допуска, но при этом существенно увеличивается допуск составляющих звеньев. Метод исходит из предположения, что сочетания действительных размеров составляющих звеньев, входящих в размерную цепь, носят случайный характер, и большая часть значений звеньев группируется около координаты середины поля допуска. Для такого метода применяется вероятностный способ расчета.
Слайд 4При анализе размерных цепей обычно решают два класса задач:
Обратная задача - задача,
При анализе размерных цепей обычно решают два класса задач:
Обратная задача - задача,

Прямая задача - задача, при которой заданы параметры замыкающего звена (номинальное значение, допустимые отклонения и т.д.) и требуется определить параметры составляющих звеньев (проектная задача).
Прямая и обратная задача могут решаться двумя методами: расчетом на «максимум – минимум» и вероятностным расчетом (так как размеры деталей в партии – случайные величины в пределах допуска).
Расчет на «максимум – минимум» проводится для малозвенных цепей с повышенной точностью.
При расчете размерных цепей с числом составляющих звеньев более трех целесообразно принять в основу достижения точности метод неполной взаимозаменяемости с использованием вероятностного расчета.
При использований метода неполной взаимозаменяемостн требуемая точность обеспечивается у заранее обусловленной части объектов. Расчет производится с учетом фактического распределения истинных размеров внутри полей допусков и вероятности их различных сочетаний при сборке.
Слайд 13Метод неполной взаимозаменяемости исходит из предложения, что сочетание действительных размеров составляющих звеньев
Метод неполной взаимозаменяемости исходит из предложения, что сочетание действительных размеров составляющих звеньев

Замыкающее звено размерной цепи принимается за случайную величину, являющуюся суммой независимых случайных составляющих звеньев размерной цепи.
При расчете по вероятностному методу поле допуска замыкающего звена рассчитывается по формуле:
tΔ - коэффициент риска (аргумент функции Лапласа), выбирается из таблицы в зависимости от принятого процента брака Р.
λ - коэффициент относительного рассеяния составляющих звеньев, зависит от закона распределения размера составляющего звена.
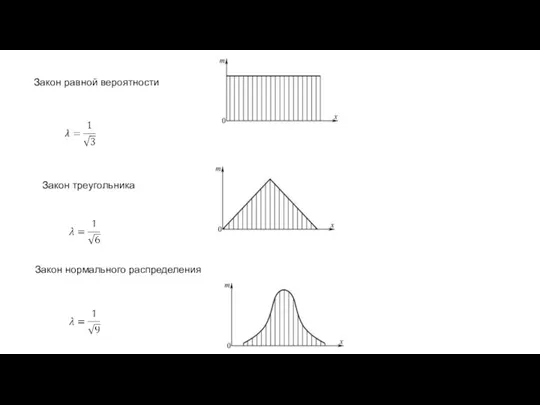
Слайд 14Закон равной вероятности
Закон треугольника
Закон равной вероятности
Закон треугольника
Слайд 15
λ - коэффициент относительного рассеяния, зависит от закона распределения размера.
Координата середины
λ - коэффициент относительного рассеяния, зависит от закона распределения размера.
Координата середины

Слайд 16Уравнение номинальных размеров цепи:
АΔ=А1-А2-А3=190-150-40=0 мм
Проверяем возможность обеспечения точности замыкающего звена
Уравнение номинальных размеров цепи:
АΔ=А1-А2-А3=190-150-40=0 мм
Проверяем возможность обеспечения точности замыкающего звена

TΔ=T1+T2+T3=0,20+0,10+0,06=0,36 м
Так как расчетное значение TΔ больше заданного (0,36>0.2), то полная взаимозаменяемость при заданных допусках составляющих звеньев не обеспечивается.
Порядок выполнения расчетов размерных цепей
На основе анализа и расчета размерных цепей установить наиболее целесообразный метод сборки.
Проверяем возможность сборки по методу полной взаимозаменяемости, рассчитывая размерную цепь на максимум – минимум.
Слайд 18Прямая (проектная) задача расчета размерных цепей
Рассчитать допуски на размеры составляющих звеньев
Прямая (проектная) задача расчета размерных цепей
Рассчитать допуски на размеры составляющих звеньев

Решение этой задачи неоднозначное, можно решать одним из способов. Способ равных допусков применяют, когда все размеры цепи входят в один интервал, в примере размеры из разных интервалов.
Слайд 204 задание
Расчет размерных цепей
1. Рассчитать заданную размерную цепь по методу полной взаимозаменяемости
4 задание
Расчет размерных цепей
1. Рассчитать заданную размерную цепь по методу полной взаимозаменяемости

3. Решить обратную задачу вероятностным методом (размеры составляющих звеньев и замыкающего звена имеют нормальный закон распределения).







 НАЙДИ
НАЙДИ Правила приема в Томский государственный университет систем управления и радиоэлектроники (ТУСУР)
Правила приема в Томский государственный университет систем управления и радиоэлектроники (ТУСУР) Продукция
Продукция Эрик Ван Эгераат
Эрик Ван Эгераат Презентация на тему Грузия
Презентация на тему Грузия Шоколад «за и против»
Шоколад «за и против» ХВС 5 класс
ХВС 5 класс Тема любви в творчестве Куприна и Бунина…
Тема любви в творчестве Куприна и Бунина… Русские ювелирные украшения XVII-XX веков
Русские ювелирные украшения XVII-XX веков Тема: «Логика как наука»
Тема: «Логика как наука» Как человек изменил землю (5 класс)
Как человек изменил землю (5 класс) Мраморная вуаль в скульптуре
Мраморная вуаль в скульптуре C наступающим праздником! И пусть Новый Год войдет в дом с такими же яркими лучами...
C наступающим праздником! И пусть Новый Год войдет в дом с такими же яркими лучами... Презентация на тему празднованию 70-летия Великой Победы над фашистской Германией
Презентация на тему празднованию 70-летия Великой Победы над фашистской Германией Местные повестки 21 в гимназииLokaltagesordnung 21 im GymnasiumStaatsgymnasium, Kostjukovitschi
Местные повестки 21 в гимназииLokaltagesordnung 21 im GymnasiumStaatsgymnasium, Kostjukovitschi Дробові вирази (1)
Дробові вирази (1) Лес - наше богатство!
Лес - наше богатство! Математический вечер
Математический вечер Кожаные куртки
Кожаные куртки Информация и знания
Информация и знания Конституционный Суд РФ
Конституционный Суд РФ "Вместе выше радуги"
"Вместе выше радуги" Что такое «КАЛЕВАЛА»?
Что такое «КАЛЕВАЛА»? Из опыта применения методики здоровьесберегающего обучения на уроках географии в рамках национальной образовательной инициатив
Из опыта применения методики здоровьесберегающего обучения на уроках географии в рамках национальной образовательной инициатив Презентация на тему Наибольший общий делитель. Взаимно простые числа
Презентация на тему Наибольший общий делитель. Взаимно простые числа  Смысловые группы наречий
Смысловые группы наречий Диагностика наследственных заболеваний
Диагностика наследственных заболеваний Филологический анализ текста
Филологический анализ текста