Содержание
- 2. Гипотеза Применяли ли древние математики терему Пифагора при решении задач? В каких задачах древности используется теорема
- 3. Мы провели исследование Мы провели исследовательскую работу, привлекая информационные технологии, в поиске исторических задач на тему
- 4. Алгоритм решения задач по теореме Пифагора Внимательно прочти задачу, разберись с условием. По условию сделай чертеж.
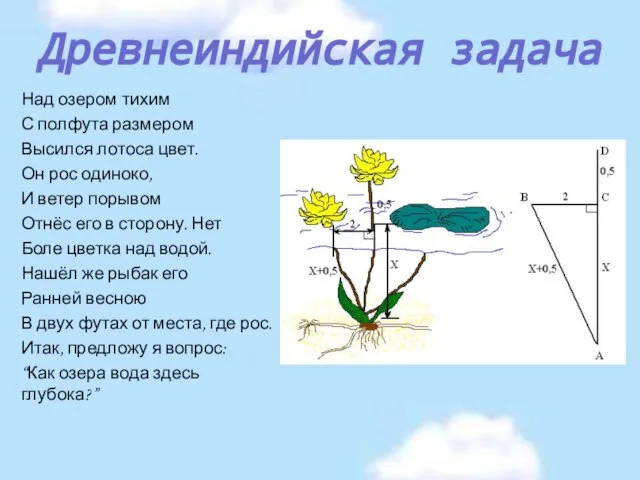
- 5. Над озером тихим С полфута размером Высился лотоса цвет. Он рос одиноко, И ветер порывом Отнёс
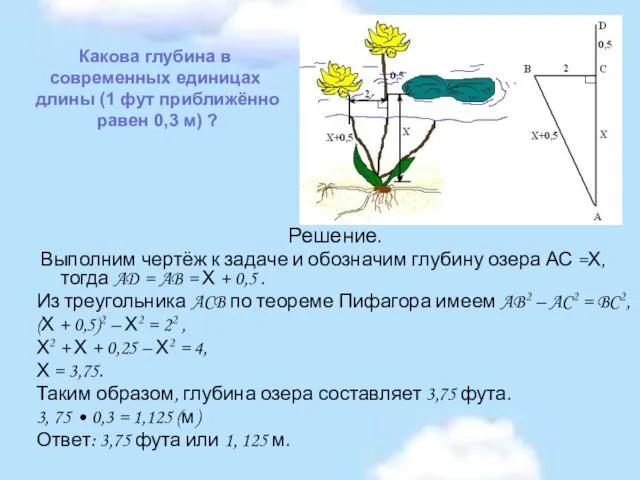
- 6. Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ? Решение. Выполним чертёж
- 7. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И
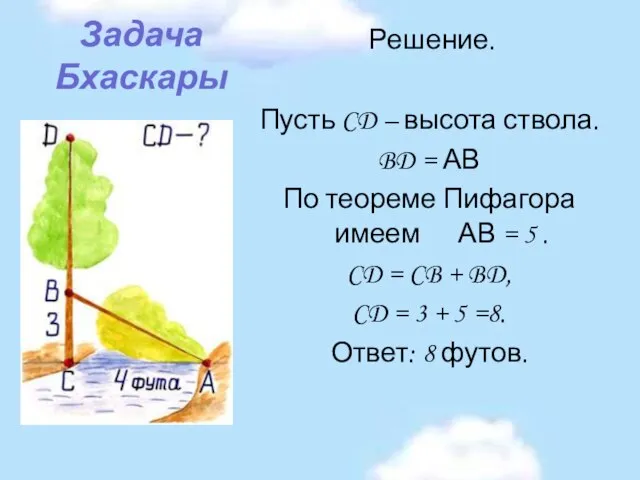
- 8. Задача Бхаскары Решение. Пусть CD – высота ствола. BD = АВ По теореме Пифагора имеем АВ
- 9. На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой –
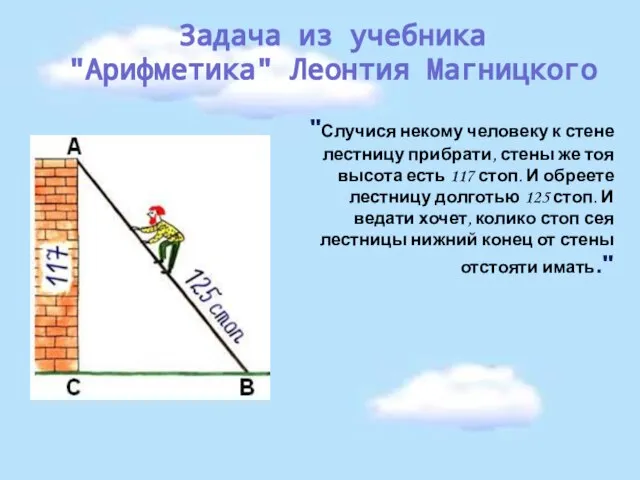
- 10. "Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете
- 11. "Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который
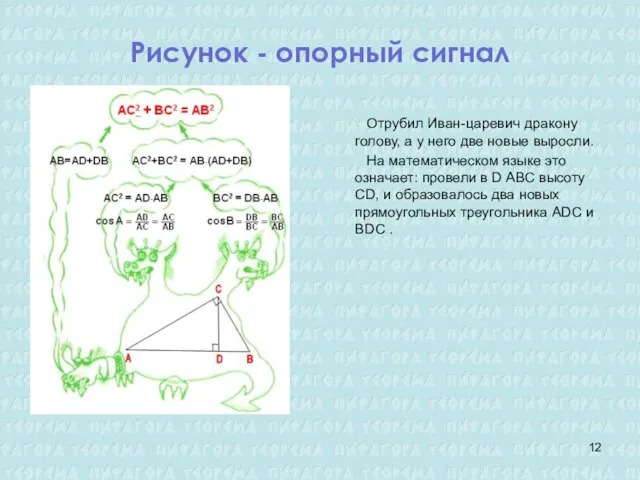
- 12. Рисунок - опорный сигнал Отрубил Иван-царевич дракону голову, а у него две новые выросли. На математическом
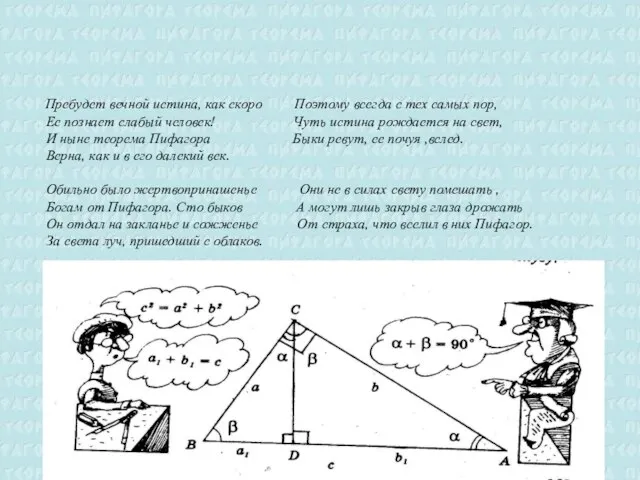
- 13. Теорема Пифагора – одна из главных теорем геометрии, потому что с её помощью можно решить множество
- 16. Скачать презентацию







 Курляндский В.В. СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОГРАФИЧЕСКИХ ШИРОТ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ,
Курляндский В.В. СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОГРАФИЧЕСКИХ ШИРОТ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ,  Внимание подросток!
Внимание подросток! презентация лого Горбатиков (1) (1)
презентация лого Горбатиков (1) (1) Экологическая игра « Поле чудес»
Экологическая игра « Поле чудес» ВИДЫ ПРОГРАММДЛЯ МОЛОДЫХ СПЕЦИАЛИСТОВ, РЕАЛИЗУЕМЫЕ В СОВРЕМЕННЫХ КОМПАНИЯХ
ВИДЫ ПРОГРАММДЛЯ МОЛОДЫХ СПЕЦИАЛИСТОВ, РЕАЛИЗУЕМЫЕ В СОВРЕМЕННЫХ КОМПАНИЯХ Совершенствование управления конкурентоспособностью предприятия
Совершенствование управления конкурентоспособностью предприятия Introduction
Introduction Гидроизоляция блочного фундамента (включая демонтаж)
Гидроизоляция блочного фундамента (включая демонтаж) Правила и нормы поведения в обществе
Правила и нормы поведения в обществе Презентация на тему Фредерик Шопен
Презентация на тему Фредерик Шопен Компания DominiSoft www.dominisoft.ru Компания “БУКА” www.buka.ru www.bukasoft.ru
Компания DominiSoft www.dominisoft.ru Компания “БУКА” www.buka.ru www.bukasoft.ru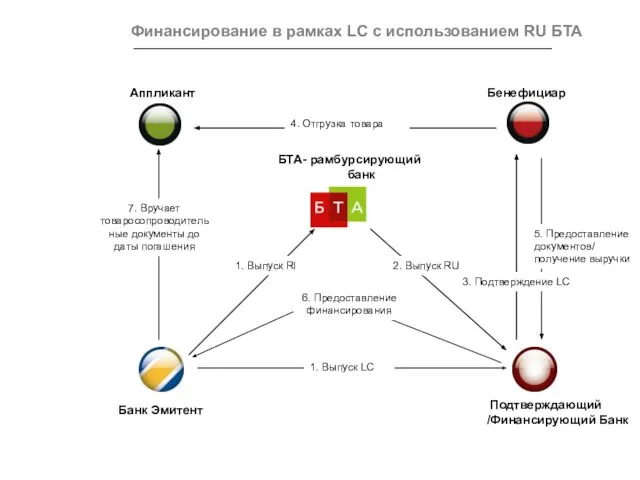 Финансирование в рамках LC с использованием RU БТА
Финансирование в рамках LC с использованием RU БТА Презентация на тему Методы исследования
Презентация на тему Методы исследования Организация совместной работы музыкального руководителя и специалистов ДОУ
Организация совместной работы музыкального руководителя и специалистов ДОУ Ручная уборка территорий
Ручная уборка территорий Публичное и частное право
Публичное и частное право Комплексные разработки
Комплексные разработки Конфликт & согласие. Особенности конфликтных ситуаций
Конфликт & согласие. Особенности конфликтных ситуаций DEFINITION OF LAW
DEFINITION OF LAW  Организационное стимулирование. Условия для внедрения мотивации персонала
Организационное стимулирование. Условия для внедрения мотивации персонала Царство Животны. Тип Моллюски. Классы - Брюхоногие Двустворчатые Головоногие
Царство Животны. Тип Моллюски. Классы - Брюхоногие Двустворчатые Головоногие Развитие учения об отдельных видах следов. Тема №4
Развитие учения об отдельных видах следов. Тема №4 Односоставные предложения
Односоставные предложения The system of state bodies of lebanon
The system of state bodies of lebanon Экологическое страхование и оценка рисков
Экологическое страхование и оценка рисков Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Современное антикоррозионное покрытие
Современное антикоррозионное покрытие МЕТРОПОЛИТЕН
МЕТРОПОЛИТЕН