Защита сумасбродных проектов

Законы случайного
Всей нашей жизнью правят законы вероятности.
Кто знает, что ждет нас завтра- выигрыш в лотерее или несчастный случай?
Точно предсказать будущее невозможно.
Обладая всей нужной информацией, можно просчитать степень вероятности того или иного события.

Лист Мебиуса
Лист Мёбиуса - топологический объект, простейшая односторонняя поверхность с краем.
Попасть из одной точки этой поверхности в любую другую можно, не пересекая края.
Лист Мёбиуса иногда называют прародителем символа бесконечности.
Лента Мёбиуса обладает любопытными свойствами.

Лист Мебиуса

Чтобы получить ленту Мёбиуса, мы поворачиваем полоску бумаги на пол оборота.А интересно что у вас получится, если вы склеите ленту, сделав полный оборот , и получившееся кольцо разрежете пополам вдоль?
Попробуйте прорезать в полосе щель и продеть сквозь нее один конец полосы. (как показано на рисунке) А теперь попробуйте продолжить разрез вдоль всей ленты. Что у вас получилось, если не секрет?
Опыты
Склейте два кольца- одно простое и лист Мёбиуса. Разрежьте каждое из них пополам вдоль. Что у Вас получилось?

Проблема четырех красок
В математике великое множество нерешенных задач.
В 1976г. с помощью компьютеров математиками В. Хикеном и К. Аппелем была разрешена знаменитая проблема четырех красок.
Доказали. Что любую географическую карту можно окрасить в четыре цвета так, что страны , имеющие общую границу, будут окрашены в разные цвета.

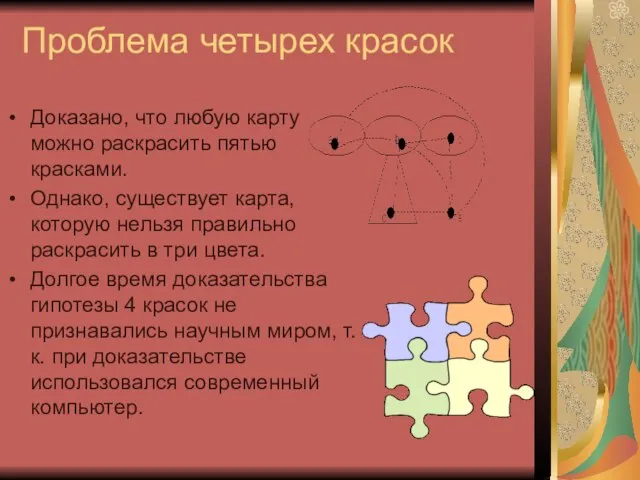
Проблема четырех красок
Доказано, что любую карту можно раскрасить пятью красками.
Однако, существует карта, которую нельзя правильно раскрасить в три цвета.
Долгое время доказательства гипотезы 4 красок не признавались научным миром, т. к. при доказательстве использовался современный компьютер.

Треугольник Рело
Рассмотрим правильный треугольник .На каждой стороне построим дугу окружности, радиусом равным длине стороны.
Эта кривая и носит имя "треугольник Рело".
В житейском смысле постоянная ширина кривой означает, что если сделать катки с таким профилем, то книжка будет катиться по ним, не шелохнувшись

Треугольник Рело
эта геометрическая фигура имеет интересные приложения в механике

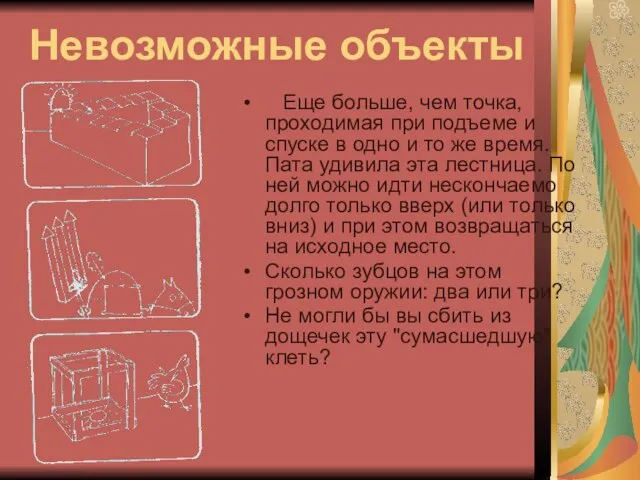
Невозможные объекты
Еще больше, чем точка, проходимая при подъеме и спуске в одно и то же время. Пата удивила эта лестница. По ней можно идти нескончаемо долго только вверх (или только вниз) и при этом возвращаться на исходное место.
Сколько зубцов на этом грозном оружии: два или три?
Не могли бы вы сбить из дощечек эту "сумасшедшую" клеть?

Несуществующие объекты
"Если бы вы только знали, какие видения посещают меня в ночной тьме... Иногда моя неспособность сделать их зримыми буквально сводит меня с ума. По сравнению с этими мыслями каждая отдельная гравюра или рисунок - это полная неудача, только мельчайшая частица необъятного целого".

НЕВОЗМОЖНАЯ РЕАЛЬНОСТЬ

Математические фокусы
Веселый счет.
1000,
40,
1000,
30,
1000,
20,
1000,
10.
?

Математичиский фокус Дэвида Копперфильда
Фокусы такого типа называются фокусами с предопределенным выбором.
Узнав секрет фокуса, вы можете модернизировать его по собственному усмотрению.

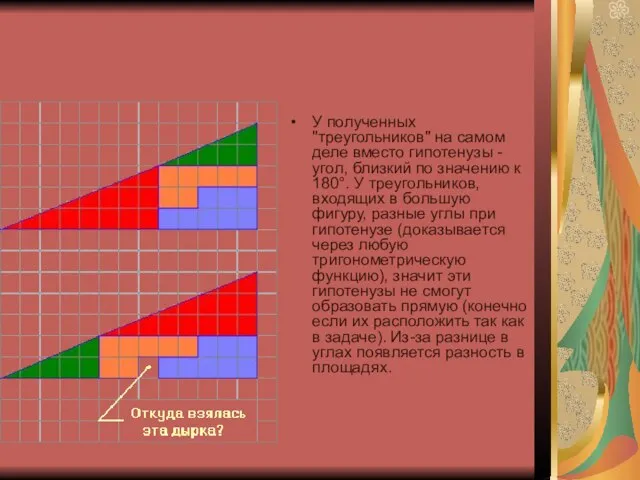
У полученных "треугольников" на самом деле вместо гипотенузы - угол, близкий по значению к 180°. У треугольников, входящих в большую фигуру, разные углы при гипотенузе (доказывается через любую тригонометрическую функцию), значит эти гипотенузы не смогут образовать прямую (конечно если их расположить так как в задаче). Из-за разнице в углах появляется разность в площадях.

Задачи- шутки
Тут затеи и задачи,
Игры, шутки, всё для вас!
Пожелаю вам удачи.
За работу, в добрый час!

1.Сколько кошек сидит на стуле, если известно, что сумма чисел их хвостов и лап есть однозначное число? При этом по крайней мере одна кошка находится на стуле наверняка
2.Однажды Винни-Пух целый день ходил в гости к Кролику. Сообрази, где Винни-Пух заночевал, если известно, что расстояние между своим домом и норой Кролика медвежонок преодолел нечётное число раз.
3.Что вырвалось из груди ученика, когда учитель заставил его сто раз написать букву "Н"?
4.У одноголового змея один хвост. Сколько хвостов у трёхголового змея? А у девятиголового? А у стоголового?
5.Какое число получится, если перемножить число горбов у двугорбого верблюда, хоботов у слона, шей у вертишейки, панцирей у черепахи, клювов у дятла, крыльев у воробья, глаз у зайца, хвостов у головастика, гребешков у петуха, лап у медведя, бивней у мамонта, копыт у лошади, ног у сороконожки, щупалец у осьминога, зубов у крокодила, иголок у ежа и рогов у осла?
6.За неделю гусыня снесла число яиц большее, чем 6, но меньшее, чем 8. Сколько утят вылупилось из этих яиц?
7.Спрячь руки за спину и ответь: сколько у тебя пальцев?