Содержание
- 2. Изучить историю возникновения тригонометрии и понять, как зарождались математические понятия, связанные с ней Узнать, в каких
- 3. «Великая книга природы может быть прочтена только теми, кто знает язык, на котором она написана, и
- 4. Какие житейские ситуации повлияли на возникновение тригонометрических функций?
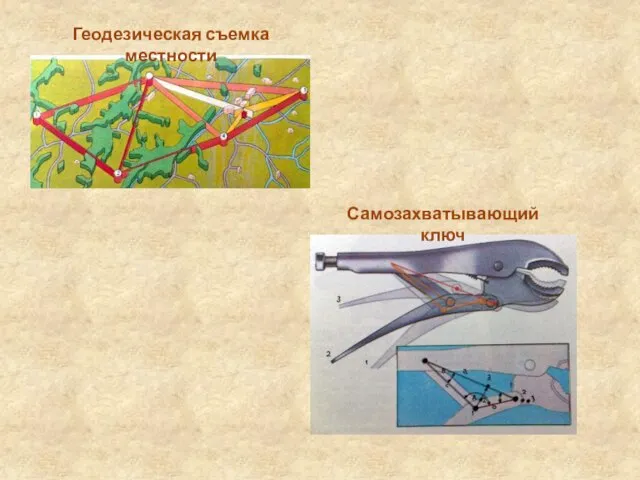
- 5. Геодезическая съемка местности Самозахватывающий ключ
- 6. Квадрант Пучок радиоволн
- 7. Современные инженеры и техники, создающие различные машины и механизмы, в которых происходит преобразование круговых движений в
- 8. Представим себе нить в форме окружности. Разрежем её и растянем за концы. Тонкая нить С Длина
- 9. Верхушка головы - где 1,7м рост человека. Ноги прошли путь , где R радиус земного шара.
- 10. Задача 2. Вечером автобус на повороте радиусом закругления R = 100 м освещает дорогу светом, расходящимся
- 11. Модель 2. Радианное измерение дуг и углов Существуют различные способы измерения дуг и углов. Механики чаще
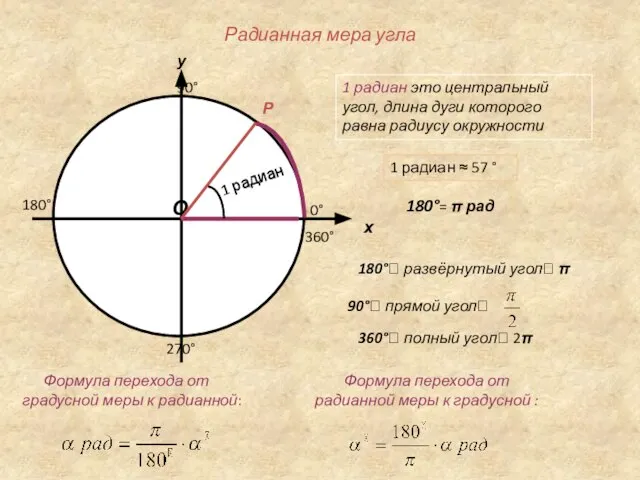
- 12. Радианная мера угла у О Р х 1 радиан это центральный угол, длина дуги которого равна
- 13. Задача 2. Маховик трактора имеет в диаметре 0,5 м и делает 1980 оборотов в минуту. а)
- 14. Модель 3. Координатная окружность Периодический характер имеют многие световые, звуковые, электромагнитные явления, а также целый ряд
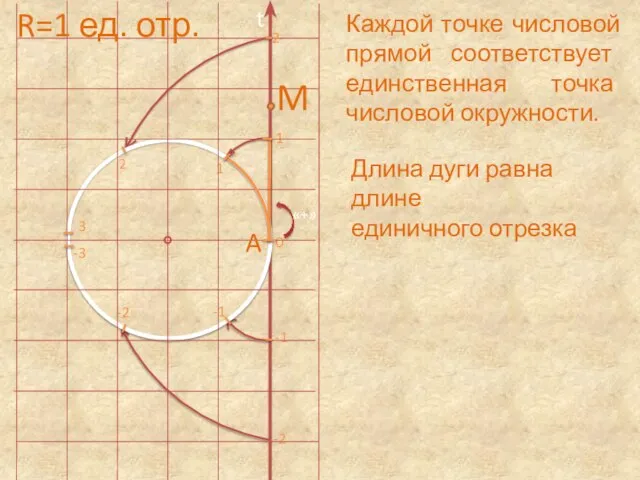
- 15. 0 1 2 2 1 -1 -2 -2 3 -1 -3 t Каждой точке числовой прямой
- 16. Задача. Колесо автомобиля вращается с угловой скоростью π рад/с. Найти число оборотов: а) за 25с б)
- 17. Колебания - один из самых распространенных процессов в природе и технике. Даже наше каждодневное хождение на
- 18. Задача. Для двух шкивов, соединенных ременной передачей вычислите углы α при прямой передаче и β при
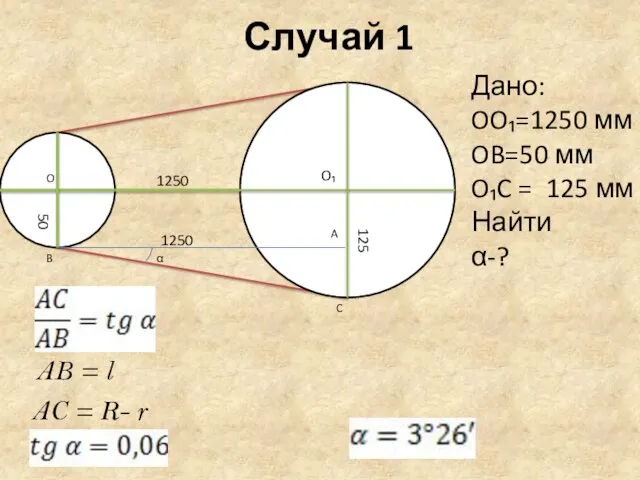
- 19. Случай 1 1250 1250 125 50 A C B O O₁ α Дано: OO₁=1250 мм OB=50
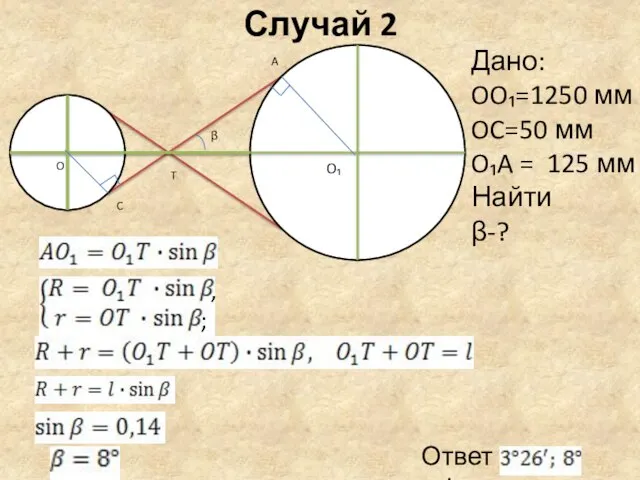
- 20. Ответ: Случай 2 O₁ O T C A β Дано: OO₁=1250 мм OC=50 мм O₁A =
- 21. Простые гармонические колебания описываются с помощью функций синус и косинус: А – амплитуда, ω - частота,
- 22. Существует легенда о том, что еще в древнем Китае монахи день за днем вели наблюдения за
- 23. Проанализировав эту информацию, можно построить следующую модель: где t – время, Tr – периоды, r –
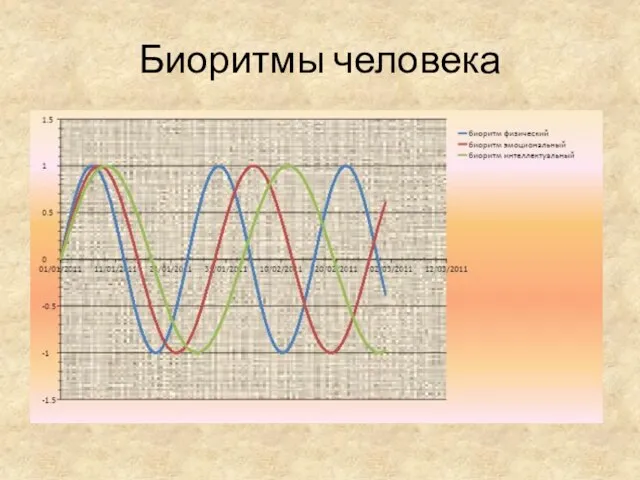
- 25. Биоритмы человека
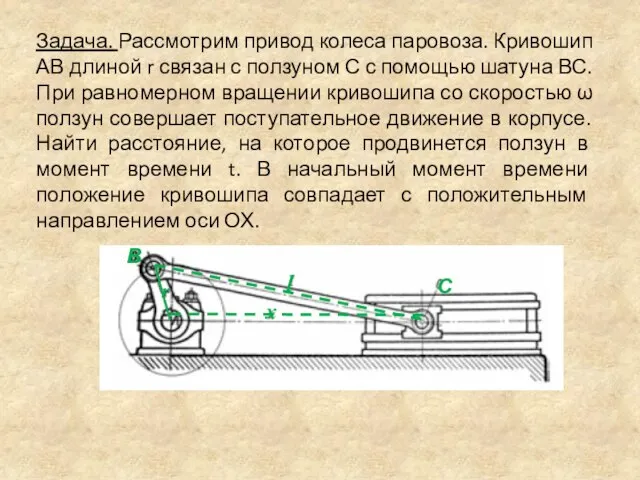
- 26. Задача. Рассмотрим привод колеса паровоза. Кривошип АВ длиной r связан с ползуном С с помощью шатуна
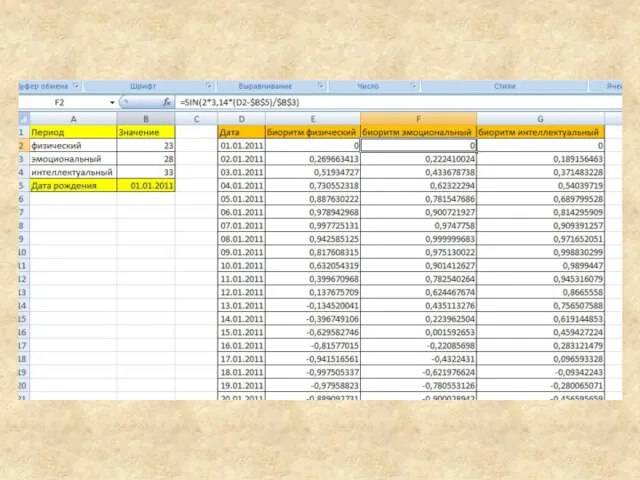
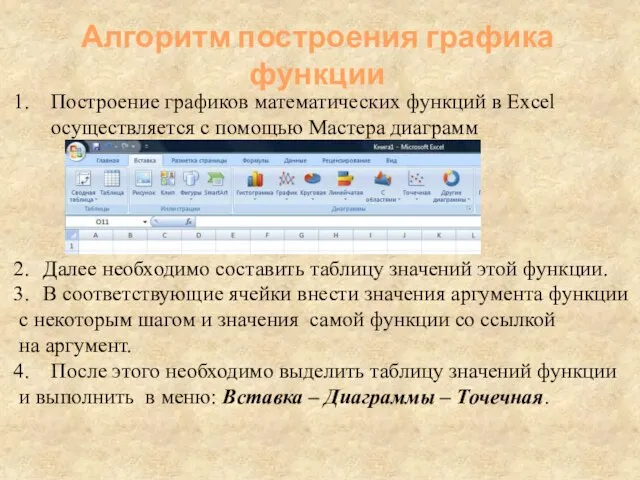
- 27. Построение графиков математических функций в Excel осуществляется с помощью Мастера диаграмм Далее необходимо составить таблицу значений
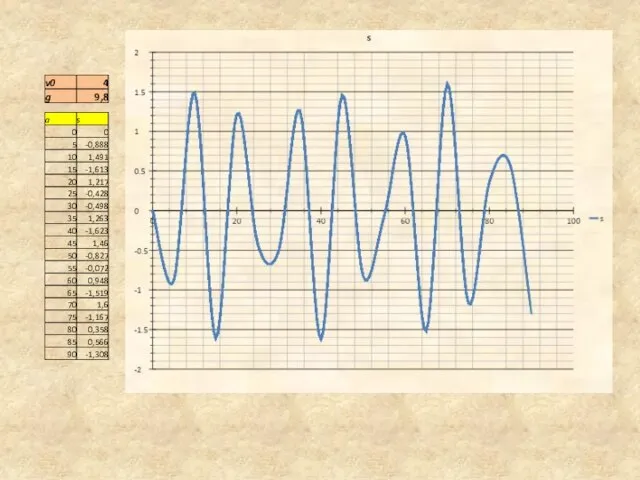
- 28. Графики тригонометрических функций
- 30. Тригонометрические уравнения и неравенства
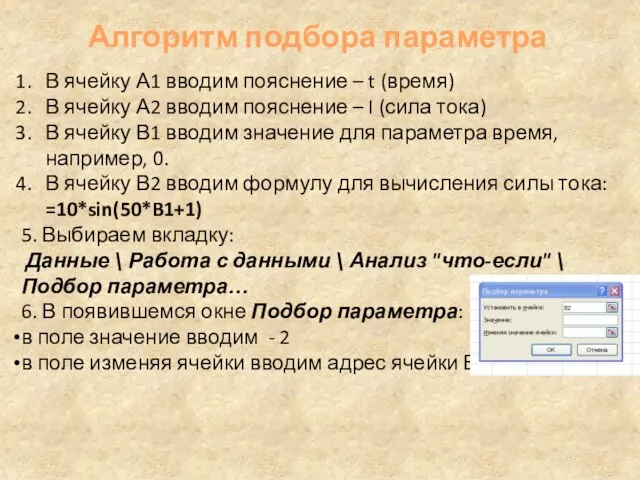
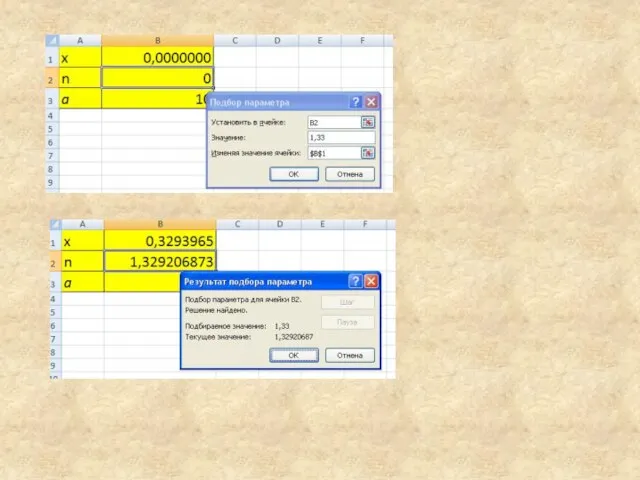
- 31. Алгоритм подбора параметра В ячейку А1 вводим пояснение – t (время) В ячейку А2 вводим пояснение
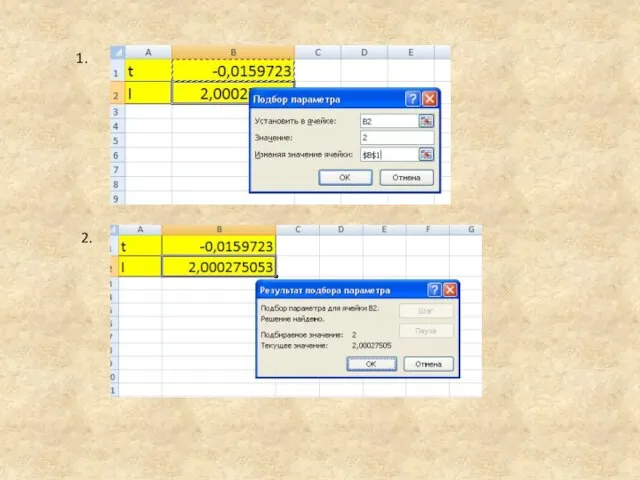
- 32. 1. 2.
- 33. Задача. Как направить луч на границу двух сред, чтобы угол падения луча превышал угол преломления на
- 36. Скачать презентацию




















 Мой друг – спорт. Верю – не верю
Мой друг – спорт. Верю – не верю Клаус Шваб Четвертая промышленная революция
Клаус Шваб Четвертая промышленная революция Потребности и расходы. Управление семейным бюджетом
Потребности и расходы. Управление семейным бюджетом Презентация на тему Музыкальные инструменты на Руси
Презентация на тему Музыкальные инструменты на Руси Презентация на тему Что общего у разных растений
Презентация на тему Что общего у разных растений  Права на чужие вещи
Права на чужие вещи  Привлекательная инвестиция. Производство электроэнергии и тепла в Вологодской области, Россия
Привлекательная инвестиция. Производство электроэнергии и тепла в Вологодской области, Россия Презентация на тему Сравнительное наблюдение за прорастанием семян
Презентация на тему Сравнительное наблюдение за прорастанием семян Так в чем же польза катания на коньках?
Так в чем же польза катания на коньках? Презентация на тему Магнитные свойства вещества
Презентация на тему Магнитные свойства вещества Organizatsia
Organizatsia ТЕМА №5
ТЕМА №5 Презентация на тему Внутреннее строение млекопитающих
Презентация на тему Внутреннее строение млекопитающих Past Continuos Tense
Past Continuos Tense Лес и его обитатели
Лес и его обитатели бух учет шамов
бух учет шамов Векторная графика
Векторная графика Растение в интерьере жилого дома
Растение в интерьере жилого дома Поморские небылицы
Поморские небылицы Презентация на тему Биогеоценоз и биоценоз
Презентация на тему Биогеоценоз и биоценоз Станция обнаружения целей (СОЦ). Блок череспериодной компенсации и индикатор кругового обзора. Эксплуатация ЧПК и ИКО
Станция обнаружения целей (СОЦ). Блок череспериодной компенсации и индикатор кругового обзора. Эксплуатация ЧПК и ИКО Монастыри России
Монастыри России Презентация на тему Бурундуки
Презентация на тему Бурундуки Презентация по технике безопасности
Презентация по технике безопасности Старинные занимательные математические задачи
Старинные занимательные математические задачи Воздействие на документ. Изменения свойств бумаги. Люминесценция. Воздействие на тонер
Воздействие на документ. Изменения свойств бумаги. Люминесценция. Воздействие на тонер Своя игра 2
Своя игра 2 вставь пропущенную букву
вставь пропущенную букву