Слайд 2
§1 Классификация типов знаний

Слайд 3 Для определения понятия «знание» существует множество вариантов вариантов. Рассмотрим некоторые из вариантов

определения:
Определение 1. Знание – это результат полученный познанием.
Определение 2. Знание – это система суждений с принципами и единой организацией, основанная на объективной закономерности.
Определение 3. Знание – это формализованная информация на которую используют и на которую ссылаются в процессе логического вывода.
Слайд 4 Традиционно выделяют восемь типов знаний:
1. Базовые знания – они связаны с объективным

восприятием окружающего мира и обычно обозначают реальные объекты этого мира, знание такого типа изначально считается достоверным и не требует доказательств.
2. Утверждения и определения – это знания основанные на базовых объектах, также рассматривается как достоверное.
3. Концепции – перегруппировка базовых объектов, концепции могут быть различными и каждая из них строится по своему собственному правилу.
Слайд 5 4. Отношения – позволяет установить свойства базовых объектов, определить отношение между базовыми

объектами и концепциями, также определять свойства. Отношение не является абсолютно достоверным, поэтому можно утверждать о их правдоподобности и связывать достоверность отношение к конкретной ситуацией.
5. Теоремы и правила перезаписи – это знание которое определяет правила перехода от одних знаний к другим. И позволяет управлять стратегией логического вывода.
6. Алгоритмы решения – эти знания предназначены для решения конкретных задач. Особенностью их является то, что эти знания всегда строго упорядочены, и теряют всякий смысл вне контекста алгоритма.
Слайд 6 7. Стратегии и эвристики – это врожденные или приобретенные знания, которые позволяют

найти эффективное решение в некоторых конкретных ситуациях. Информация этого типа, обычно используется в порядке обратном приобретенному, при этом знания этого типа не обладают общностью и абсолютной достоверностью. Т.е. они могут быть истинны или ложны, в зависимости от конкретной ситуации.
8. Метазнания – знания о знаниях. Они представляют собой информацию о том, как работать со знаниями, как их представить. Как использовать в процессе вывода. Как проверить достоверность.
Слайд 8
Определение. Формальная система представляет собой совокупность чисто абстрактных объектов, не связанных с

внешним миром, в которой представлены правила оперирования множеством символов только в синтаксической трактовке без учета смыслового содержания.
Слайд 9 Формирование строгой формальной теории осуществляется в следующем порядке:
1. Задается конечное множество символов,

которые образуют алфавит формальной системы.
2. Устанавливаются процедуры построения формул формальной системы.
Слайд 10 3. Устанавливается множество аксиом, т.е. формул, истинность которых не требует доказательства. Обычно

к ним относят те утверждения, которые полагаются очевидными по самой природе рассматриваемых понятий.
4. Устанавливается конечное множество правил вывода, которые позволяют получать новые формулы из некоторого множества известных формул. В общем случае эти правила могут быть представлены в следующем виде что означает: из множества истинных формул указанных в левой части выражения, следует истинность формул правой части выражения.
Слайд 11
Определение. Интерпретация представляет собой распространение исходных положений какой-либо формальной системы на реальный

мир. Интерпретация придает смысл каждому символу формальной системы и устанавливает взаимно однозначное соответствие между символами формальной системы и реальными объектами. Теоремы формальной системы, будучи интерпретированы, становятся после этого утверждениями в обычном смысле слова, и в этом случае уже можно делать выводы об их истинности или ложности.










 Презентация на тему Основные инфекционные заболевания и их профилактика
Презентация на тему Основные инфекционные заболевания и их профилактика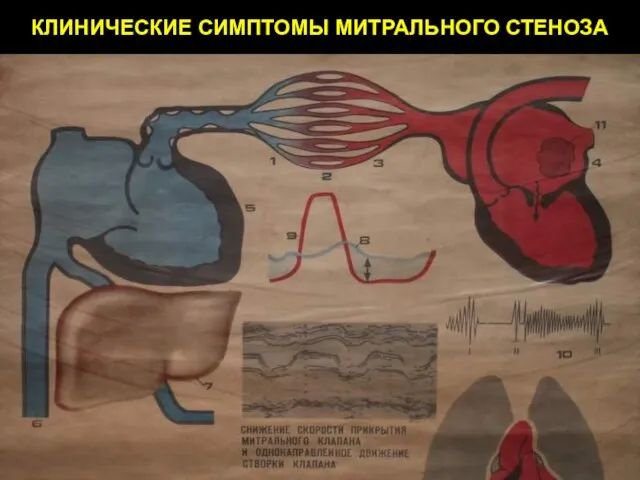 Митральные пороки
Митральные пороки  Влияние компьютерных игр на здоровье младших школьников и определение компьютерной зависимости
Влияние компьютерных игр на здоровье младших школьников и определение компьютерной зависимости Презентация на тему Пальчиковая гимнастика
Презентация на тему Пальчиковая гимнастика  “Мастерская для инноваций”
“Мастерская для инноваций” В каких странах говорят на английском языке?
В каких странах говорят на английском языке? В ожидании Рождества. Фотоальбом
В ожидании Рождества. Фотоальбом В.Б. Тарасов МГТУ им. Н.Э.Баумана, Кафедра «Компьютерные системы автоматизации производства» e-mail:
В.Б. Тарасов МГТУ им. Н.Э.Баумана, Кафедра «Компьютерные системы автоматизации производства» e-mail:  Административная ответственность
Административная ответственность МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ ВЕРБАЛЬНЫХ И НЕВЕРБАЛЬНЫХ ЕДИНИЦ В ДИАЛОГЕ II Б. ДЕЙКТИЧЕСКИЕ ЖЕСТЫ И РЕЧЕВЫЕ АКТЫ Крейдлин Г. Е. (РГГУ,
МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ ВЕРБАЛЬНЫХ И НЕВЕРБАЛЬНЫХ ЕДИНИЦ В ДИАЛОГЕ II Б. ДЕЙКТИЧЕСКИЕ ЖЕСТЫ И РЕЧЕВЫЕ АКТЫ Крейдлин Г. Е. (РГГУ,  Технология как часть общечеловеческой культуры
Технология как часть общечеловеческой культуры Коммуникационные технологии
Коммуникационные технологии  Атмосфера: значение, строение, изучение
Атмосфера: значение, строение, изучение Презентация на тему Вода в природе 3 класс
Презентация на тему Вода в природе 3 класс  Презентация на тему Фалес Милетский
Презентация на тему Фалес Милетский Реки
Реки Блинчики-Мск. Проект
Блинчики-Мск. Проект Презентация на тему Чтобы путь был счастливым (3 класс)
Презентация на тему Чтобы путь был счастливым (3 класс) Развитие социальной психологии
Развитие социальной психологии проект ккт
проект ккт Установка коннектора компрессора на новых корейских компрессорах!
Установка коннектора компрессора на новых корейских компрессорах! Я РАДА ПРИВЕТСТВОВАТЬ ВАС НА УРОКЕ ФИЗИКИ
Я РАДА ПРИВЕТСТВОВАТЬ ВАС НА УРОКЕ ФИЗИКИ общая характеристика растений
общая характеристика растений Новогодний хороводНам очень веселоВозьмёмся за руки.. - презентация
Новогодний хороводНам очень веселоВозьмёмся за руки.. - презентация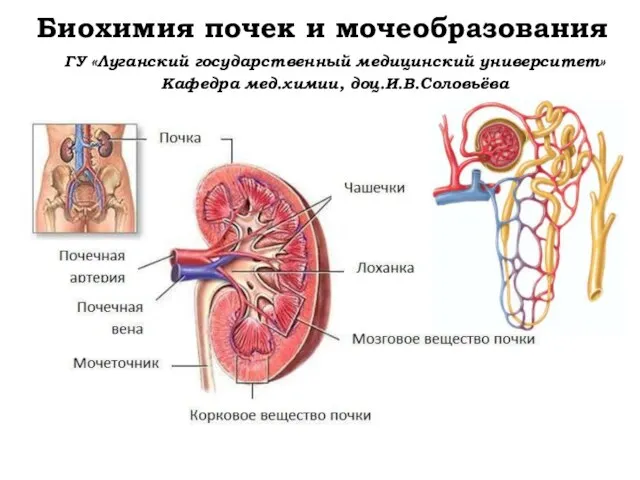 Биохимия почек и мочеобразования
Биохимия почек и мочеобразования Сертификация систем качества
Сертификация систем качества Презентация на тему Экологические факторы. Антропогенное воздействие на экосистемы
Презентация на тему Экологические факторы. Антропогенное воздействие на экосистемы Птичья азбука
Птичья азбука