Знания о системах счисления и двоичном представлении информации в памяти компьютера

Сколько единиц содержится в двоичной записи результата выражения:
(2·108)2010 – 42011 + 22012?
Свойство степени с основанием 2
Количество 0:
20=12 0
21=102 1
22=1002 2
2n=1000...0002 n
n
16 раздел

Приводим все числа к основанию 2
108=810= 2310
4 = 22
(2·108)2010 – 42011 + 22012= (2·23)2010 – (22)2011 + 22012, учитывая, что 2·23=24, получим:
Сколько единиц содержится в двоичной записи результата выражения:
(2·108)2010 – 42011 + 22012?

Применяем правило возведения степени в степень:
(24)2010 – (22)2011 + 22012= 28040 – 24022 + 22012
28040= 100000000 …02 (8040 нулей)
24022=100000000 …02 (4022 нуля)
22012=100000000 …02 (2012 нулей)
Сколько единиц содержится в двоичной записи результата выражения:
(2·108)2010 – 42011 + 22012?

Вычитаем из числа 28040 число 24022, но сначала рассмотрим пример:
Видим, что этот пример выполняет 25 – 22.
В результате 2 нуля и (5-2) единицы.
Найдите количество нулей и единиц в разности:
28040 – 24022
28040 – 24022 + 22012
1 0 0 0 0 02
- 1 0 02
1 1 1 0 02

28040 - 24022
4018 единицы в начале и 4022 нуля в конце!
Теперь прибавим к результату 22012.
Заметим, что в этом числе одна единица и остальные 2012 разрядов - нули.
В результате суммы в конечный результат добавляется ещё одна единица.
Следовательно, в двоичной записи выражения получится 4019 единиц.
Ответ: 4019

Ещё пример 16 задания:
Сколько единиц в двоичной записи числа
42016 – 22018 + 8800 – 80
Решение:
(22)2016 – 22018 + (23)800 – 26 – 24
24032 – 22018 + 22400 – 26 – 24
Перестроим слагаемые в порядке уменьшения степеней двойки:
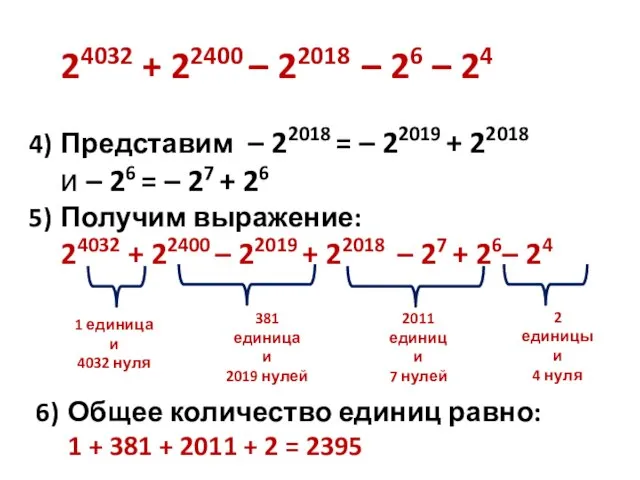
24032 + 22400 – 22018 – 26 – 24

24032 + 22400 – 22018 – 26 – 24
4) Представим – 22018 = – 22019 + 22018
и – 26 = – 27 + 26
5) Получим выражение:
24032 + 22400 – 22019 + 22018 – 27 + 26– 24
1 единица
и
4032 нуля
381 единица
и
2019 нулей
2011 единиц
и
7 нулей
2 единицы
и
4 нуля
6) Общее количество единиц равно:
1 + 381 + 2011 + 2 = 2395

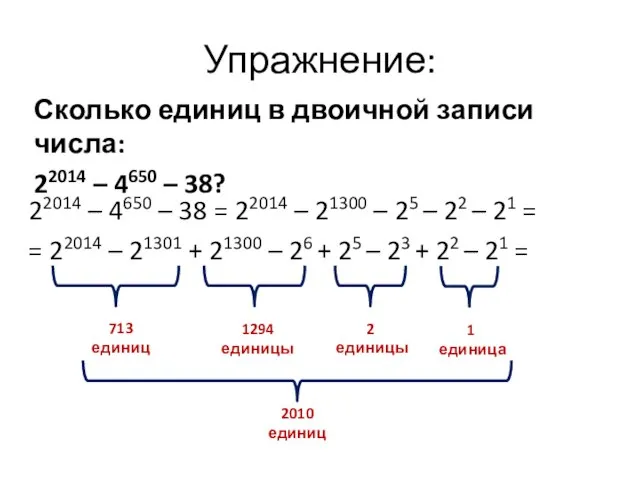
Упражнение:
Сколько единиц в двоичной записи числа:
22014 – 4650 – 38?
22014 – 4650 – 38 = 22014 – 21300 – 25 – 22 – 21 =
= 22014 – 21301 + 21300 – 26 + 25 – 23 + 22 – 21 =

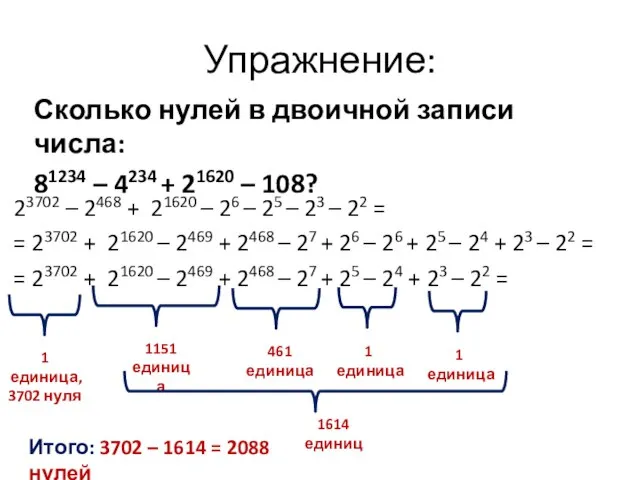
Упражнение:
Сколько нулей в двоичной записи числа:
81234 – 4234 + 21620 – 108?
23702 – 2468 + 21620 – 26 – 25 – 23 – 22 =
= 23702 + 21620 – 2469 + 2468 – 27 + 26 – 26 + 25 – 24 + 23 – 22 =
= 23702 + 21620 – 2469 + 2468 – 27 + 25 – 24 + 23 – 22 =
Итого: 3702 – 1614 = 2088 нулей

Значение арифметического выражения:
4∙254 – 54 + 14 записали в системе счисления с основанием 5. Какова сумма цифр содержащихся в этой записи? Ответ укажите в десятичной системе.
4*58= 4000000005 (8 нулей)
1*54= 100005 (4 нуля)
2*51= 205 4*50=45
400000005 4000000245
245 100005
4000000245 3444400245
+
-
Сумма цифр: 3+20+2= 25
Упражнение:

Упражнение:
Значение арифметического выражения:
922 + 366 – 18 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Решение:
1*344 + 1*366 – 2*32

Решение:
Сколько цифр «2» содержится в этой записи?
1*366= 100000000000000 …03 (66 нулей)
1*344= 100000000 …03 (44 нуля)
2*32= 2003
100000000000000 …03 100…00100…..0003
100000000 …03 2003
1 1 100…00022..21003
1*366 + 1*344 – 2*32
+
-

Упражнение:
Вычислите: 102212113 – 38389 + 3 27
Ответ запишите в десятичной системе счисления
Раздел 1
Девятеричная и троичная системы счисления являются родственными системами записи чисел. Составим таблицу:
Переведём троичное число в девятеричную систему:
102212113=38549
9
9
9
Вычислим разность:
=1*91 + 5+90=1410
Переведём в десятичную систему :
327=310. Последнее действие: 14 + 3 = 17.