Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Πιθανότητα Ενδεχομένων
Πολλές φορές η πληροφόρηση για την έκβαση ενός πειράματος δεν είναι μηδενική
Μερική πληροφόρηση για το αποτέλεσμα ενός πειράματος
Υπολογισμός πιθανότητας αποτελέσματος λαμβάνοντας υπόψιν τη μερική πληροφόρηση: Δεσμευμένη Πιθανότητα
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Δεσμευμένη Πιθανότητα
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

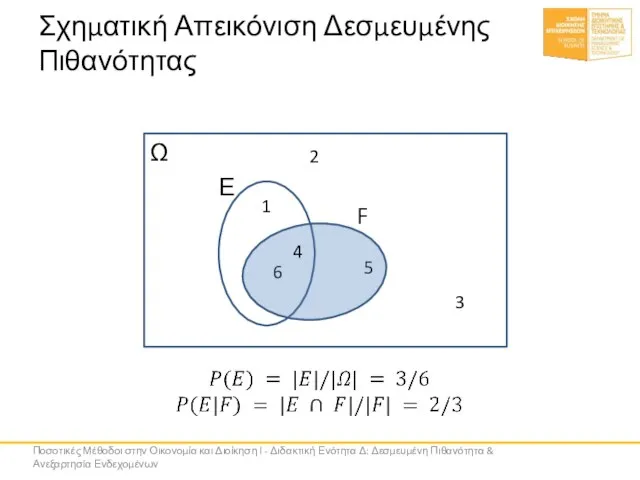
Σχηματική Απεικόνιση Δεσμευμένης Πιθανότητας
Ε
1
6
5
F
2
3
4
Ω
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Δεσμευμένη Πιθανότητα
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 1
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 1
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 2
Πρόβλημα
Τραβάμε διαδοχικά φύλλα από μία τράπουλα
α) Ποια η πιθανότητα να τραβήξουμε έναν άσσο
β) Ποια η πιθανότητα να τραβήξουμε έναν άσσο με δεδομένο πως το πρώτο φύλλο ήταν άσσος
γ) Ποια η πιθανότητα να τραβήξουμε έναν άσσο με δεδομένο πως το πρώτο φύλλο δεν ήταν άσσος
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 2
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 2
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 3
Πρόβλημα
Στρίψιμο δίκαιου νομίσματος (Κ/Γ) 2 φορές
α) Ποια η πιθανότητα να φέρουμε Κ και στις 2 ρίψεις (ΚΚ)?
β) Ποια η δεσμευμένη πιθανότητα να φέρουμε ΚΚ με δεδομένο πως στο 1ο στρίψιμο φέραμε Κ?
γ) Ποια η δεσμευμένη πιθανότητα να φέρουμε ΚΚ με δεδομένο πως σε ένα στρίψιμο φέραμε Κ?
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 3
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 4
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 4
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

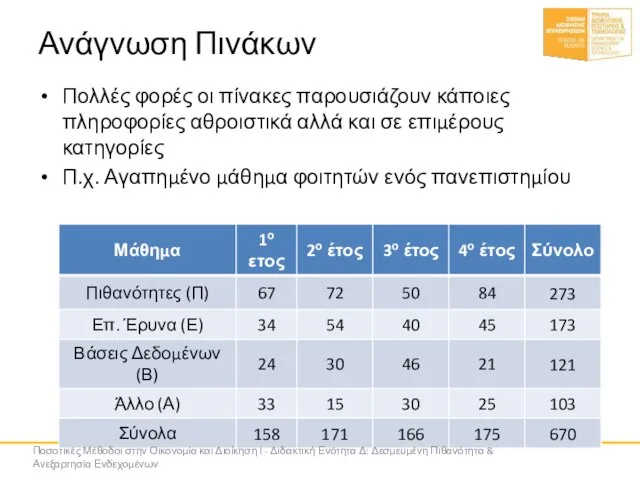
Ανάγνωση Πινάκων
Πολλές φορές οι πίνακες παρουσιάζουν κάποιες πληροφορίες αθροιστικά αλλά και σε επιμέρους κατηγορίες
Π.χ. Αγαπημένο μάθημα φοιτητών ενός πανεπιστημίου
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

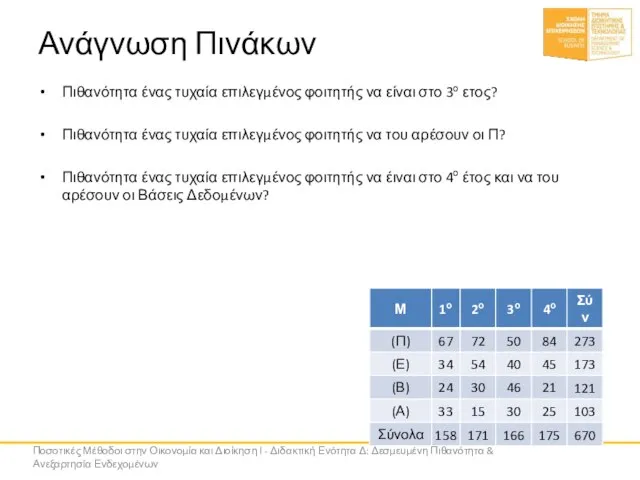
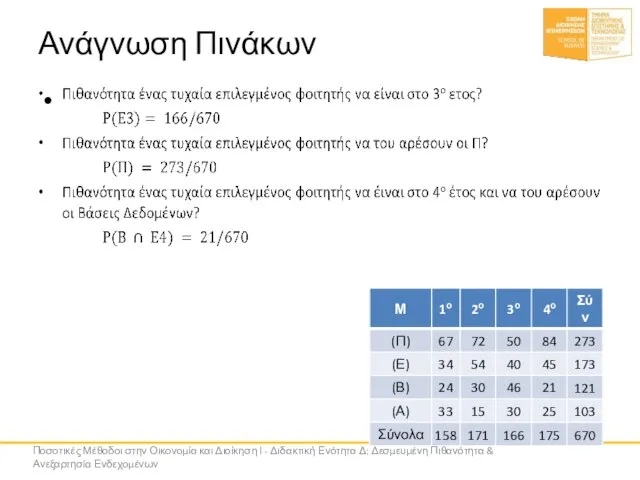
Ανάγνωση Πινάκων
Πιθανότητα ένας τυχαία επιλεγμένος φοιτητής να είναι στο 3ο ετος?
Πιθανότητα ένας τυχαία επιλεγμένος φοιτητής να του αρέσουν οι Π?
Πιθανότητα ένας τυχαία επιλεγμένος φοιτητής να έιναι στο 4ο έτος και να του αρέσουν οι Βάσεις Δεδομένων?
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ανάγνωση Πινάκων
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ανάγνωση Πινάκων
Πιθανότητα ένας τυχαία επιλεγμένος φοιτητής να του αρέσουν οι Π με δεδομένο ότι είναι στο 1ο έτος?
Πιθανότητα ένας τυχαία επιλεγμένος φοιτητής να είναι στο 2ο έτος με δεδομένο ότι το αγαπημένο του μάθημα είναι η Επιχ. Έρευνα?
Πιθανότητα ένας τυχαία επιλεγμένος φοιτητής να είναι στο 1ο ή στο 3ο έτος με δεδομένο ότι το αγαπημένο του μάθημα δεν είναι οι Π, οι ΒΔ κ η Ε?
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ανάγνωση Πινάκων
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 5
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 5
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 5
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 5
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Πολλαπλασιαστικός Κανόνας
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 6
Πρόβλημα
Θέλουμε να αγοράσουμε ένα βιβλίο εκ των Α και Β
Θεωρούμε πως το Α θα μας αρέσει κατά 70%
Θεωρουμε πως το Β θα μας αρέσει κατά 50%
Το Α είναι ακριβότερο, έτσι θα το αποφασίσουμε στρίβοντας ένα νόμισμα.
Ποια η πιθανότητα να αγοράσουμε και να μας αρέσει το Α?
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 6
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 7
Πρόβλημα
Μία τράπουλα με 52 φύλλα κόβεται τυχαία σε 4 στοίβες των 13 φύλλων
Ποια η πιθανότητα κάθε στοίβα να έχει έναν άσσο
Σημείωση: Το πρόβλημα το έχουμε ξαναδεί στην προηγούμενη ενότητα μετρώντας τα εμπλεκόμενα σύνολα.
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 7
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 7
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 8
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 8
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Θεώρημα Ολικής Πιθανότητας
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Θεώρημα Ολικής Πιθανότητας
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Τύπος του Bayes
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

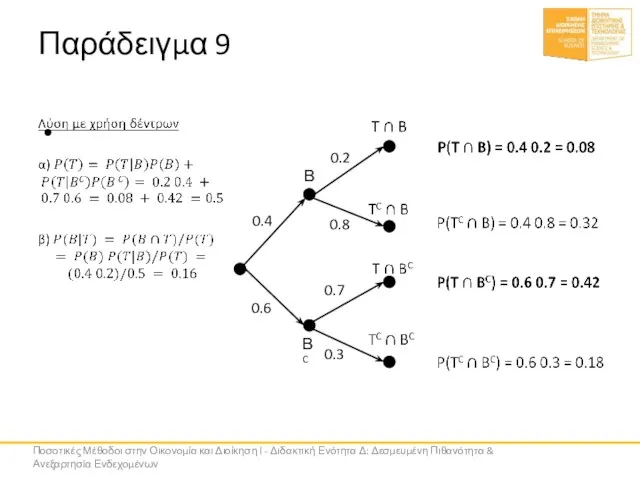
Παράδειγμα 9
Πρόβλημα
Αν βρέξει, ο Γιώργος βγαινει για τρέξιμο με πιθανότητα 20%
Αν δε βρέξει, βγαινει για τρέξιμο με πιθανότητα 70%
Στην πόλη του Γιώργου το 60% των ημερών δε βρέχει
Ποια η πιθανότητα ο Γιώργος να πάει για τρέξιμο μία τυχαία μέρα;
Αν μία μέρα γνωρίζουμε πως έτρεξε ποια η πιθανότητα αυτή τη μέρα να είχε βρέξει;
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 9
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 9
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 10
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

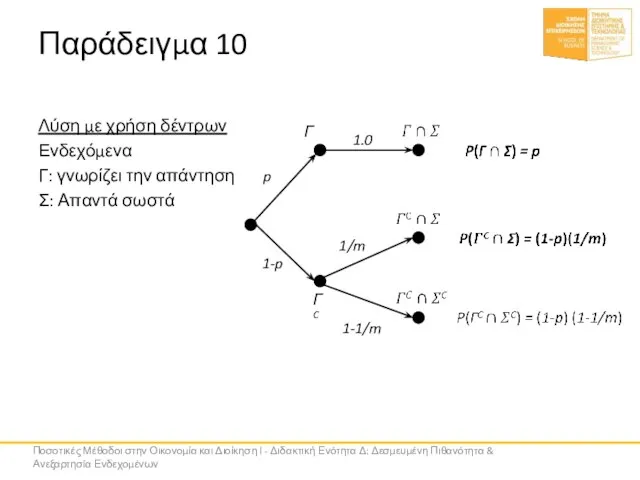
Παράδειγμα 10
Λύση με χρήση δέντρων
Ενδεχόμενα
Γ: γνωρίζει την απάντηση
Σ: Απαντά σωστά
Γ
ΓC
p
1-p
1.0
1/m
1-1/m
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 10
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 11
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 11
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

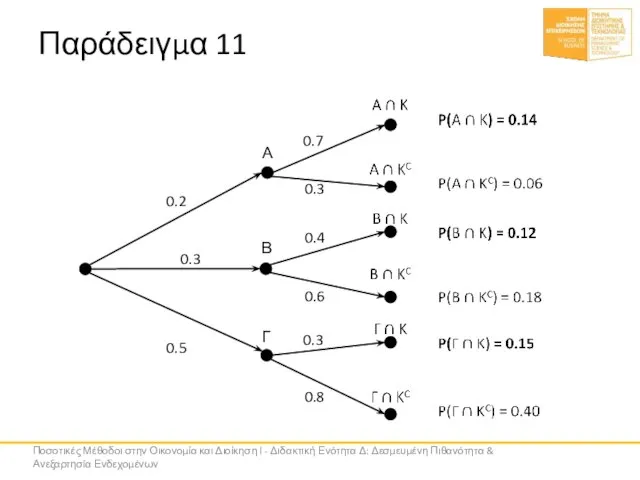
Α
Β
0.7
0.3
0.4
0.6
Γ
0.2
0.8
0.3
0.5
0.3
Παράδειγμα 11
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

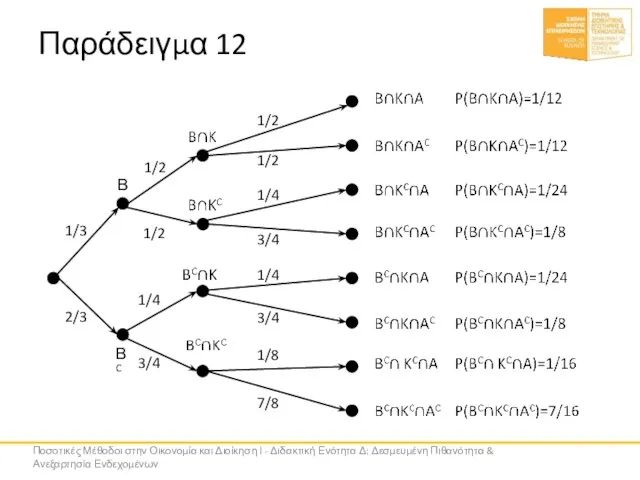
Παράδειγμα 12
Πρόβλημα
Σε μία πόλη βρέχει το 1/3 των ημερών
Όταν βρέχει, οι δρόμοι έχουν κίνηση με πιθανότητα 50%, ενώ η πιθανότητα κίνησης υποδιπλασιάζεται όταν δε βρέχει.
Όταν βρέχει και έχει κίνηση αργώ στην εργασία μου με πιθανότητα 50%
Αντίθετα, όταν δε βρέχει και δεν έχει κίνηση αργώ στη δουλειά μόνο 1 στις 8 φορές
Σε όλες τις άλλες περιπτώσεις αργώ κατά 25%
α) Ποια η πιθανότητα πως δε βρέχει και έχει αυξημένη κίνηση και φτάνω στη δουλειά στην ώρα μου?
β) Ποια η πιθανότητα να φτάσω αργά στη δουλειά μου?
γ) Με δεδομένο ότι άργησα, ποια η πιθανότητα να έβρεξε τη συγκεκριμένη μέρα?
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 12
Β
ΒC
1/3
2/3
1/2
1/2
1/4
3/4
1/2
1/8
1/4
1/4
3/4
3/4
7/8
1/2
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 12
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 12
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ανεξάρτησία Ενδεχομένων
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ανεξάρτησία Ενδεχομένων
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ανεξάρτησία Ενδεχομένων
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 13
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 13
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 14
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 15
Πρόβλημα
Ρίχνουμε δύο δίκαια εξάπλευρα ζάρια Α και Β
Ποια η πιθανότητα του αθροίσματος των ζαριών είναι να είναι 6 με δεδομένο πως το πρώτο ζάρι φέρνει 1;
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 15
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ανεξαρτησία Πολλαπλών Ενδεχομένων
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 16
Πρόβλημα
Ρίχνουμε ένα δίκαιο εξάπλευρο ζάρι τρεις φορές.
Οι ρίψεις είναι ανεξάρτητες
α) Ποια η πιθανότητα να φέρουμε και τις τρεις φορές έξι?
β) Ποια η πιθανότητα να μη φέρουμε καμία φορά έξι?
γ) Ποια η πιθανότητα να φέρουμε ακριβώς δύο φορές έξι?
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 16
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 17
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 17
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 17
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 17
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Δεσμευμένη Ανεξαρτησία
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Δεσμευμένη Ανεξαρτησία
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

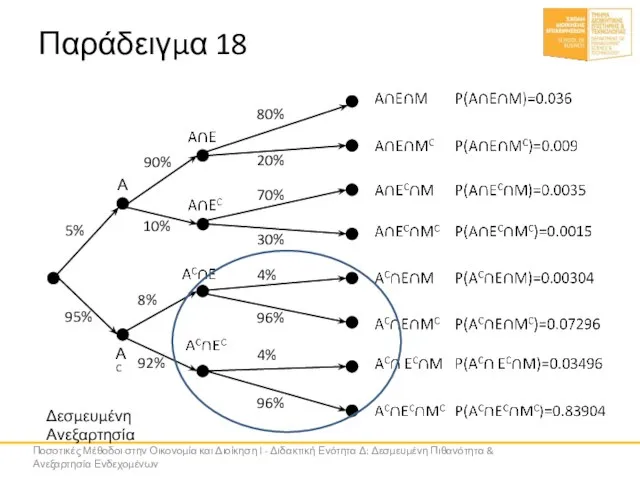
Παράδειγμα 18
Η Έλενα και η Μαρία δουλεύουν σε μία εταιρεία
Η Έλενα ζει στα ΒΠ και η Μαρία ζει στα ΝΠ
Εργάζονται σε μία εταιρία στο κέντρο της πόλης.
Μέχρι το Νοέμβριο θεωρούσαμε πως το ενδεχόμενο η Ε να αργοπορήσει στην εργασία της είναι ανεξάρτητο από το ενδεχόμενο η Μ να αργοπορήσει στην εργασία της.
Το Νοέμβριο είχαμε απεργιακές κινητοποιήσεις στα ΜΜΜ, και καταλήξαμε στα εξής
Όταν δεν έχουμε απεργίες, η Ε έχει πιθανότητα 8% να αργήσει στην εργασία της, ενώ η Μ έχει πιθανότητα 4% να αργήσει. Τα ενδεχόμενα αργοπορίας είναι ανεξάρτητα
Όταν έχουμε απεργίες, η Ε αργεί με πιθανότητα 90% και όταν η Ε αργεί, η Μ αργεί με πιθανότητα 80%. Αν η Ε φθάσει στην ώρα της, η Μ αργοπορεί με πιθανότητα 70%.
Κάθε μέρα έχει 5% πιθανότητα για απεργιακές κινητοποιήσεις στα ΜΜΜ
Ποια η πιθανότητα να αργήσει η Μ μία τυχαία μέρα;
Αν άργησε η Ε, ποια η πιθανότητα να αργήσει η Μ;
Αν άργησε η Μ, ποια η πιθανότητα να έχουμε απεργία;
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 18
Α
ΑC
5%
95%
90%
10%
8%
92%
80%
4%
4%
70%
30%
96%
96%
20%
Δεσμευμένη Ανεξαρτησία
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 18
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 19
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 20
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

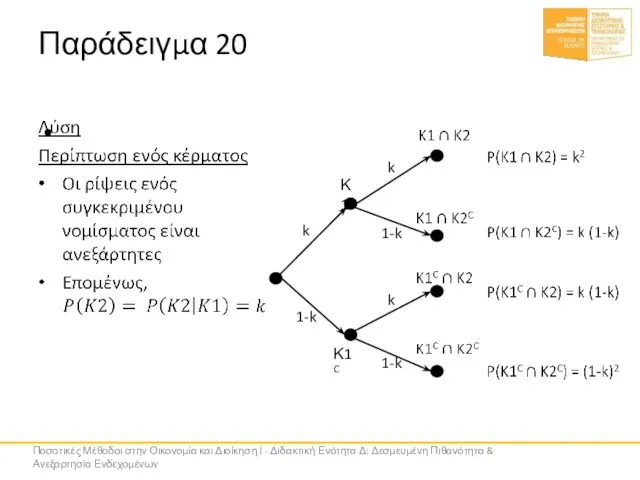
Παράδειγμα 20
Κ1
Κ1C
k
1-k
k
1-k
k
1-k
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

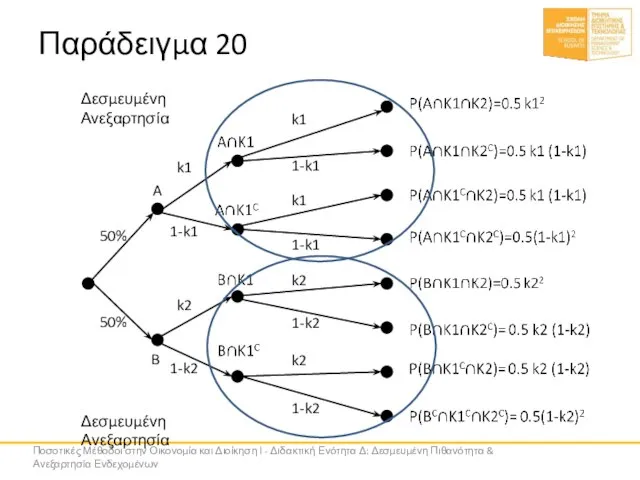
Παράδειγμα 20
A
B
50%
50%
k1
1-k1
k2
1-k2
k1
k2
k2
k1
1-k1
1-k2
1-k2
1-k1
Δεσμευμένη Ανεξαρτησία
Δεσμευμένη Ανεξαρτησία
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 20
Περίπτωση δύο κερμάτων
Ποια η πιθανότητα του Κ2 αν ξέρουμε πως το Κ1 συνέβη;
Στην απουσία γνώσης ποιο κέρμα στρίψαμε, το αποτέλεσμα της 1ης ρίψης επηρεάζει τις πιθανότητες της δεύτερης ρίψης.
Αυτό δε γίνεται γιατί η 1η ρίψη επηρεάζει τη «μηχανική» της 2ης ρίψης
Το αποτέλεσμα της 1ης ρίψης μας δίνει πληροφόρηση για το ποιο κέρμα έχει επιλεγεί τυχαία από το κουτί (π.χ. αν k2 = 0 -το κέρμα Β δεν φέρνει ποτέ Κορώνα- και εμείς είδαμε Κορώνα στην πρώτη ρίψη, πλέον ξέρουμε πως έχουμε επιλέξει το κέρμα Α).
Με δεδομένη τη μερική πληροφόρηση για το ποιο κέρμα επιλέχθηκε μπορούμε να προσεγγίσουμε με μεγαλύτερη ακρίβεια το αποτέλεσμα της 2ης ρίψης.
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 20
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 21
Πρόβλημα
Σε ένα κουτί έχουμε δύο κέρματα.
Κέρμα Α: Δίκαιο (50% Κ, 50% Γ)
Κέρμα Β: Άδικο (90% Κ, 10% Γ)
Επιλέγουμε ένα κέρμα και το δίνουμε σε ένα φίλο, ο οποίος το στρίβει 10 φορές και μας λέει πόσες κορώνες μέτρησε.
Αν μέτρησε 9 κορώνες, ποια η πιθανότητα να πήραμε το κέρμα Α?
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων

Παράδειγμα 21
Ποσοτικές Μέθοδοι στην Οικονομία και Διοίκηση Ι - Διδακτική Ενότητα Δ: Δεσμευμένη Πιθανότητα & Ανεξαρτησία Ενδεχομένων