Слайд 2ЭТАПЫ ФОРМАЛИЗАЦИИ
Формализация экономической науки осуществлялась в несколько этапов, но при этом ни

один из них нельзя считать полностью законченным — ведь экономика во многом продолжает оставаться качественной наукой. На первом из них произошло отделение формальной стороны экономического знания от содержательной стороны. Затем появились первые общеупотребительные понятия, обеспечивавшие коммуникацию («труд», «капитал», «процент», «рента» и т.п.).
Слайд 3 ЭТАП МАТЕМАТИЗАЦИИ
С внедрением математических методов понятия стали заменяться символами, а логические

связи между понятиями стали интерпретироваться на языке математических отношений — сравнения, измерения и счета: наступил этап математизации экономического знания.
Слайд 4ОПРЕДЕЛЕНИЕ МАТЕМАТИЗАЦИИ
Математизация экономической науки - это процесс внедрения в нее математических методов,

одна из разновидностей формализации [1, 10], понимаемая в самом широком аспекте как отделение формы предмета от содержания
Слайд 5Математизация экономического знания развивалась, как минимум, в трех направлениях:
первое направление —

эконометрическое (см. ниже). Задача его состояла во внедрении в экономику принципов статистического измерения и сбора данных, в численном выражении исследуемой реальности и в нахождении меры и границ этого выражения;
второе направление — построение различных математических моделей экономической реальности. Можно сказать, что для математического метода это стратегическое направление прорыва.
третье направление связано с внедрением в экономическую практику модели математического эксперимента.
Слайд 6НАПРАВЛЕНИЯ МАТЕМАТИЗАЦИИ
наконец, четвертое направление — это неметрическая математизация экономического знания, основанная на

переносе в экономическую теорию и практику принципов качественной математики.
Слайд 7ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ
Первое в истории применение математического метода в экономических исследованиях мы

находим у Уильяма Петти. В 70-е гг. XVII в. им была написана книга "Политическая арифметика", которую можно считать родоначальницей статистики и эконометрики. У. Петти объясняет свой подход так: "...вместо того, чтобы употреблять только слова в сравнительной и превосходной степени и умозрительные аргументы, я вступил на путь выражения своих мнений на языке чисел, весов и мер... используя только аргументы, идущие от чувственного опыта, и рассматривая только причины, имеющие видимые основания в природе" [6, 156].
Он требовал точного наблюдения и подсчета экономических явлений. В "Трактате о налогах и сборах" есть характерная фраза, которую можно считать девизом всей теории Петти: "Первое, что необходимо сделать, - это подсчитать...". Он ввел в политэкономию метод абстракции, когда, отвлекаясь от внешней стороны экономических явлений, от их эмпирического описания, мысль углубляется в их внутренние причинно-следственные зависимости, т.е. познает экономические законы, управляющие производством богатства.
Слайд 8ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ
Франсуа Кенэ, французский экономист и статистик XVIII в., впервые в

своей "Экономической таблице" предпринял попытку расчета "годовых доходов и авансов" страны, подобно расчетам ВНП и ЧНП в современном макроэкономическом анализе. Использование математики в работах этих экономистов можно отнести к первому этапу математизации экономической науки.
Слайд 9ЭТАПЫ МАТЕМАТИЗАЦИИ
Второй этап связан с возникновением и развитием маржиналистской математической школы. Предшественник

маржинализма французский экономист Антуан Огюстен Курно в своей работе "Исследование математических принципов теории богатства" впервые стал использовать математические приемы для выведения экономических законов, и в частности сформулировал на строгом математическом языке закон совокупного спроса, теории монополистического ценообразования, конкурентного механизма и издержек. Курно впервые ввел в научный оборот термин "экономическое равновесие".
Выдающимися представителями маржиналистской школы являются Л. Вальрас, К. Викселль, У. Джевонс, В. Парето, Ф. Эджоурт. Они считали, что только с помощью математики можно объяснить экономические явления, а экономическая наука должна занять достойное место в одном ряду с естественными науками.
Слайд 10ЭТАПЫ МАТЕМАТИЗАЦИИ
Представителями математической школы в русской политической экономии второй половины XIX -

начала XX в. были В.К. Дмитриев, Ю.И. Жуковский, Е.Е. Слуцкий, Н.А. Столяров, М.И. Туган-Барановский, А.И. Чупров и др. Основными достижениями этой школы являются: уравнение устойчивости потребительского бюджета Слуцкого, математическое исчисление полезных затрат труда с учетом межотраслевых связей Дмитриева и его же математический анализ концепции предельной полезности, математические модели Столярова и Туган-Барановского, синтезирующие маржиналистскую и трудовую теории стоимости. Многие идеи математического направления в русской политической экономии были впоследствии восприняты и развиты советской экономико-математической школой.
Слайд 11ЭТАПЫ МАТЕМАТИЗАЦИИ
Третий этап математизации начался со второй половины XX в. Если прежде

основным математическим аппаратом были производные и уравнения, то на данной стадии стали главенствовать теория множеств, векторная алгебра, исследование операций. Получили известность и признание работы Е. Домара, В. Леонтьева, М. Моришмы, X. Никайдо, Дж. фон Неймана, П. Самуэльсона, Р. Солоу, Я. Тинбергена, Р. Фриша, Р. Харрода, Дж. Хикса, К. Эрроу и других зарубежных ученых.
Слайд 12СОВЕТСКАЯ МАТЕМАТИЧЕСКАЯ ШКОЛА
Видными представителями советской экономико-математической школы, сформировавшейся к 1950 - 1960-м

гг. XX в., являлись А.Г. Аганбегян, К.А. Багриновский, А.Г. Гранберг, Л.В. Канторович, B.С. Немчинов, В.В. Новожилов, Н.Я. Петраков, Я.С. Понтрягин, Н.П. Федоренко, С.С. Шаталин и др.
Слайд 13Математическая формализация
Математическая формализация экономической науки осуществляется следующем порядке: 1) отделение формальной стороны

экономического знания от содержательной; 2) появление первых общеупотребительных понятий (труд, процент и т.п.), обеспечивающих коммуникацию; 3) математизация, т.е. замена понятий символами, интерпретация логических связей между понятиями на языке математики.
Слайд 14последствиям математизации экономической науки
К положительным последствиям математизации экономической науки могут быть отнесены:
-

точный и ясный язык научного общения, обеспечивающий коммуникацию поколений научного сообщества, что облегчает накопление и приращение знаний;
- возможность конструирования, оперирования идеализированными моделями действительности, что позволяет выделить главное, более точно описать существующие закономерности, строго определить структуру тех или иных явлений;
- возможность увидеть черты общности у разнородных явлений, т.е. применять одну и ту же модель для анализа различных явлений, меняя лишь обозначения символов;
- возможность проверки гипотез, постановки новых проблем и поиска решений;
- возможность выявить и уточнить содержание, систематизировать накопленные знания научной теории;
- синтез смежных наук.
Слайд 15последствиям математизации экономической науки
Если систематизировать отрицательные стороны математической формализации в экономической науке,

то они сводятся к следующим положениям:
- коммуникация ученых за пределами неоклассической парадигмы затруднена;
- имеет место преувеличение значения формы в ущерб содержанию экономических аргументов;
- происходят отрыв от действительности, реальных экономических проблем и потеря экономического содержания; основная задача экономической науки - понимание реальных экономических процессов и разработка мер экономической политики - остается на заднем плане или вовсе отсутствует;
- из экономического анализа исключаются наблюдаемые феномены, которые не подлежат формализации;
- формализм не приносит нового знания, а лишь позволяет интерпретировать самые простые из существующих идей, причем эта интерпретация востребована лишь узким кругом специалистов.














 Параметрические методы ценообразования Подготовила:Клеутина С., группа МЭ-092
Параметрические методы ценообразования Подготовила:Клеутина С., группа МЭ-092 Бизнес-план кофейни
Бизнес-план кофейни Методы государственного регулирования экономики
Методы государственного регулирования экономики Ординалистская, порядковая теория полезности. Лекция 7
Ординалистская, порядковая теория полезности. Лекция 7 Справочные материалы к концепции социально-экономического развития РФ до 2020 года
Справочные материалы к концепции социально-экономического развития РФ до 2020 года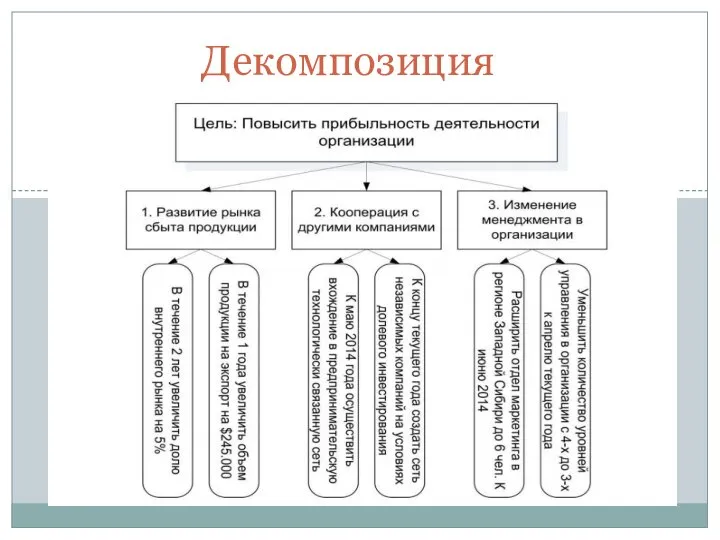 Декомпозиция. Диагностика
Декомпозиция. Диагностика Ўзбекистон Республикаси давлат мустақиллигининг ўттиз йиллик байрамини филиалда
Ўзбекистон Республикаси давлат мустақиллигининг ўттиз йиллик байрамини филиалда Платежный баланс
Платежный баланс Общероссийский конкурс Мой бизнес- моя Россия. Возрождение отечественной сельскохозяйственной продукции
Общероссийский конкурс Мой бизнес- моя Россия. Возрождение отечественной сельскохозяйственной продукции КПК Надежное будущее
КПК Надежное будущее Окупаемость инвестиций ROI
Окупаемость инвестиций ROI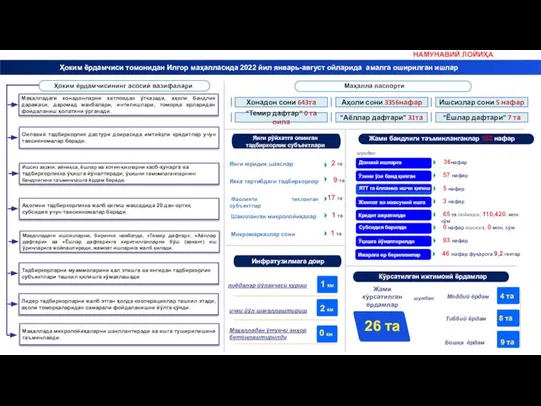 Намуна слайд ИЛГОР МФЙ 26 09 2022 й
Намуна слайд ИЛГОР МФЙ 26 09 2022 й Интегративный подход в экономике
Интегративный подход в экономике Рыночное равновесие
Рыночное равновесие Спрос и предложение
Спрос и предложение Экономическая система России
Экономическая система России Регіональний розвиток господарства США
Регіональний розвиток господарства США Валютный курс: виды и методы воздействия Выполнили: белоглазова ю., бондарева е.
Валютный курс: виды и методы воздействия Выполнили: белоглазова ю., бондарева е. Типы экономических систем (лекция 4)
Типы экономических систем (лекция 4) Рыночная система хозяйствования (экономика). Теория и практика. Лекция 1
Рыночная система хозяйствования (экономика). Теория и практика. Лекция 1 Классификация стран Зарубежной Азии
Классификация стран Зарубежной Азии Факторы производства, подготовкаа к ЕГЭ
Факторы производства, подготовкаа к ЕГЭ Трудовые ресурсы и их влияние на эффективность деятельность предприятия
Трудовые ресурсы и их влияние на эффективность деятельность предприятия Глобальные проблемы – проблема севера-юга
Глобальные проблемы – проблема севера-юга Международная торговля
Международная торговля Предложение денег Подготовила:Клеутина Светлана Группа МЭ-092
Предложение денег Подготовила:Клеутина Светлана Группа МЭ-092 Модель человека в экономике
Модель человека в экономике Задания на определение экономической грамотности в области конструирования и дизайна одежды
Задания на определение экономической грамотности в области конструирования и дизайна одежды