Содержание
- 2. 01 02 03 Способы построения индексов. Агрегатные индексы Понятие индексов ВОПРОСЫ 04 05
- 3. Индекс - представляет собой относительную величину, получаемую в результате сопоставления уровней сложных социально-экономических показателей во времени,
- 4. Индексируемая величина величина, изменение которой изучается в данном конкретном случае с помощью индекса
- 5. Способы построения индексов.
- 6. Каждая индексируемая величина имеет свое символическое обозначение: Количество единиц данного вида продукции - q Цена единицы
- 7. Индивидуальные индексы характеризуют изменение только одного элемента совокупности или
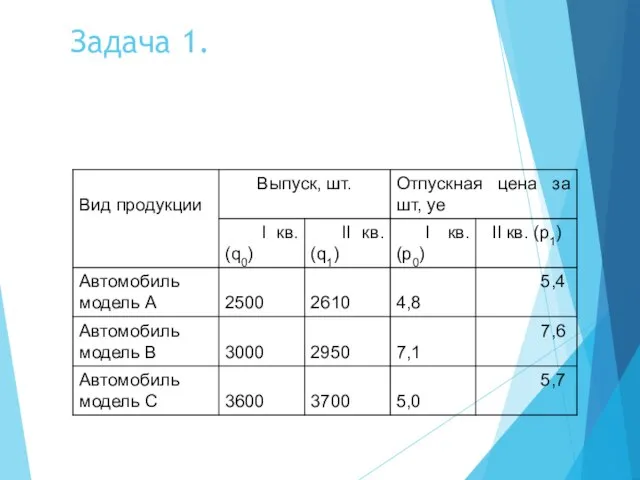
- 8. Задача 1.
- 9. Задача 1. Определить: изменение (в %) выпуска каждого вида продукции Производство автомобиля А в отчетном году
- 10. Задача 1. Производство автомобиля С в отчетном году выросло на 2,8% по сравнению с прошлым годом.
- 11. Задача № 1 Определить изменение цен ( в %) по каждому виду продукции Автомобиль модели А
- 12. Задача 1 Автомобиль модели В или 107,0% т.е. цена возросла на 7%
- 13. Задача 1 Автомобиль модели С или 114,0%, т.е. увеличение цены на 14,0%
- 14. Сводный индекс отражает изменение по всей совокупности элементов сложного явления Если индексы охватывают не все элементы
- 15. Индекс стоимости продукции (товарооборота).
- 16. показывает абсолютное изменение общей стоимости продукции за счет изменения количества продукции и цен.
- 17. Задача 1. Определить изменение товарооборота в целом по предприятию. Общая стоимость произведенной продукции увеличилась на 12,3%
- 18. Агрегатные индексы Индексы количественных показателей. Индексы качественных показателей
- 19. Внешняя отличительная особенность агрегатного индекса В числителе и в знаменателе меняется индексируемая величина. Значения другой, являющейся
- 20. Индекс физического объема товарооборота. Если мы хотим узнать как на стоимость проданной продукции повлияло изменение количества
- 21. Индекс Э. Ласпейреса
- 22. эта разность показывает абсолютное изменение общей стоимости продукции за счет изменения количества продукции
- 23. Индекс Г. Пааше
- 24. Сравнение индекса Ласпейреса и индекса Пааше Индекс Ласпейреса: В качестве коэффициента соизмерения используются цены базисного периода
- 25. Задача 1. Определить изменение выпуска продукции в целом по предприятию. Изменение количества произведенных автомобилей привело к
- 26. Индексы качественных показателей: Агрегатный индекс цен Индексируемой величиной в данном случае является цена (р), количество продукции
- 27. Индекс Пааше
- 28. Абсолютное изменение всей стоимости продукции за счет изменения цен.
- 29. Индекс Ласпейреса
- 30. Сравнение индекса цен Пааше и Ласпейреса Индекс Пааше В качестве веса используется количество товара отчетного периода
- 31. Задача1. Определить среднее изменение цен по всему ассортименту продукции. Среднее изменение цен по всему ассортименту продукции
- 32. Цепные и базисные индексы. Произведение цепных индивидуальных индексов равно последнему базисному: Базисный агрегатный индекс может быть
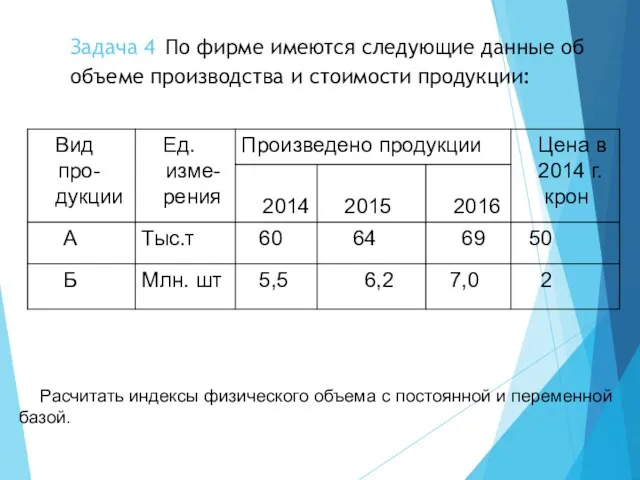
- 33. Задача 4 По фирме имеются следующие данные об объеме производства и стоимости продукции: Расчитать индексы физического
- 34. Задача 4 Расчитаем цепные индексы:
- 35. Задача № 4. Расчитаем базисные индексы
- 36. Произведение цепных индексов равно базисному 1,114*1,119 = 1,2465
- 37. Вывод: на предприятии в 2015 году по сравнению с 2014 годом наблюдается рост производства за счет
- 38. Цепные индивидуальные индексы
- 39. Базисные индивидуальные индексы
- 40. Связь индивидуальных цепных и базисных индексов.
- 41. Расчеты с помощью индексных систем недостающих индесов. или Iр * Iq = Ipq
- 42. Задача № 8. Как изменились цены, если физический объем товарооборота увеличился на 12%, а товарооборот вырос
- 43. Расчет средних арифметических индексов. Агрегатный индекс физического объема имеет вид Если из условия известна стоимость произведенной
- 44. тогда средний арифметический индекс физического объема приобретает вид:
- 45. Средний гармонический индекс цен если в качестве исходных данных имеем и изменение цен, т.е. Тогда заменяя
- 46. Получим средний гармонический индекс цен
- 47. Индексы структурных сдвигов Индекс переменного состава представляет собой соотношение средних уровней изучаемого явления, относящихся к разным
- 48. На изменение признака влияет два фактора: изменения значений осредняемого признака (x) у отдельных единиц совокупности; структурных
- 49. Индекс постоянного (фиксированного) состава отражает изолированное действие первого фактора Индекс постоянного состава может быть рассчитан и
- 50. Индекс структурных сдвигов характеризует влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака:
- 51. Связь индексов переменного, постоянного состава и структурных сдвигов Индексы переменного, постоянного состава и структурных сдвигов увязываются
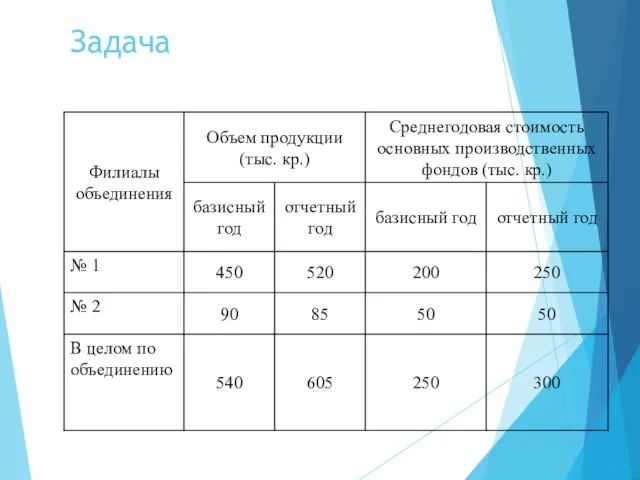
- 52. Задача
- 53. Необходимо определить: уровни фондоотдачи в отдельных филиалах объединения в отчетном и базисном периодах; средний уровень фондоотдачи
- 54. Фондоотдача обобщающий показатель, характеризующий уровень использования производственных фондов. Отдача основных производственных фондов рассчитывается путем деления объема
- 55. Где f - уровень фондоотдачи Q - объем выпускаемой продукции F - среднегодовая стоимость фондов.
- 56. Вычислим фондоотдачу для каждого филиала в отчетном и базисном периодах
- 57. Средний по объединению уровень фондоотдачи в базисном и отчетном периоде:
- 58. Динамика среднего по объединению уровня фондоотдачи: индекс переменного состава или 93,5%, т.е. фондоотдача снизилась на 6,5%
- 59. Выявим раздельное влияние каждого из факторов: уменьшение фондоотдачи в отдельных филиалах структурные изменения в распределении фондов
- 60. Таким образом, фондоотдача в среднем по филиалам объединения снизилась на 7,3%, что привело к аналогичному снижению
- 61. Проверим увязку индексов в систему
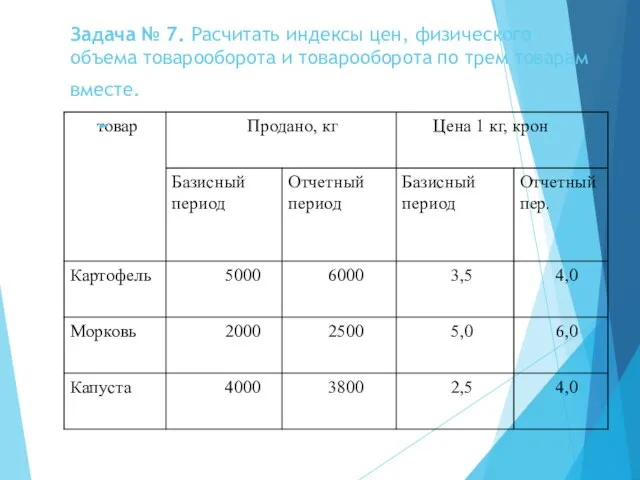
- 62. Задача № 7. Расчитать индексы цен, физического объема товарооборота и товарооборота по трем товарам вместе.
- 63. Задача № 7. Решение:
- 65. Скачать презентацию












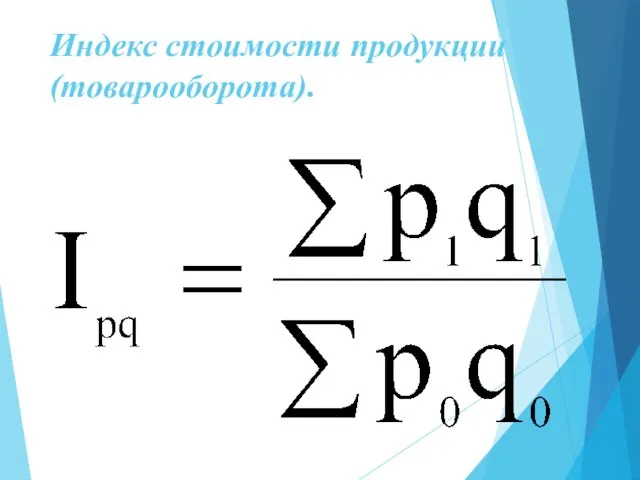







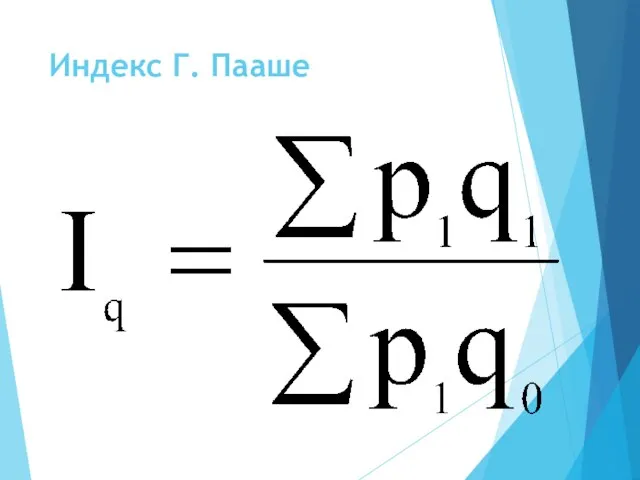



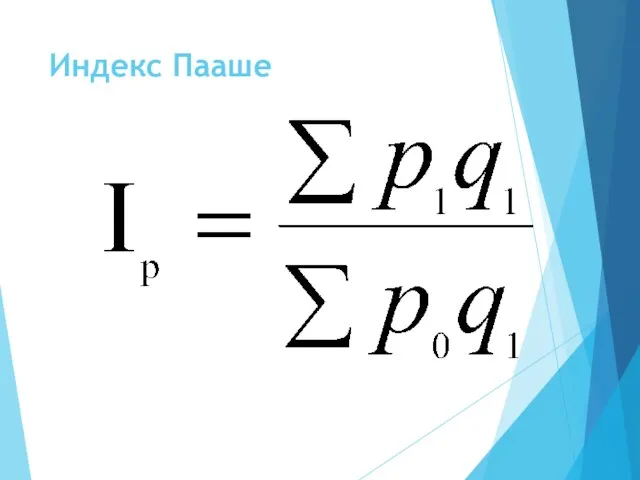

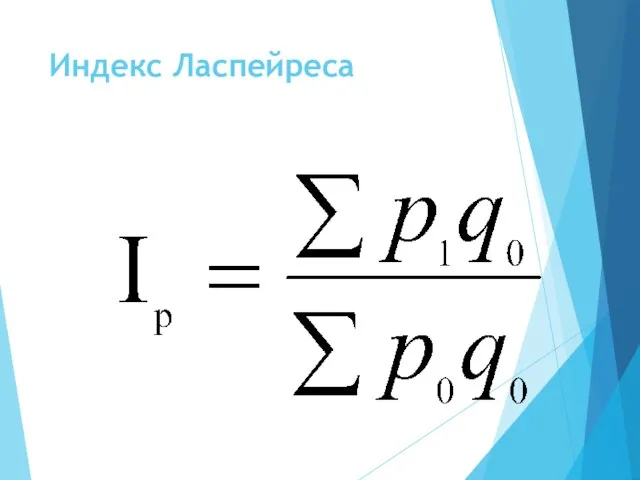































 Государственный долг, его влияние на макроэкономическую устойчивость и финансовую стабильность
Государственный долг, его влияние на макроэкономическую устойчивость и финансовую стабильность Основные фонды предприятия (часть 2)
Основные фонды предприятия (часть 2) Производство – основа экономики
Производство – основа экономики Практика по получению профессиональных умений и опыта аналитической и научно-исследовательской деятельности
Практика по получению профессиональных умений и опыта аналитической и научно-исследовательской деятельности Рынок молока Сибирского региона
Рынок молока Сибирского региона DEVELOPMENT PROSPECTS OF THE ALMATY METRO / Ppt-Presentation by Gleb K.Samoilov. – Almaty, 2016. – 47 p.
DEVELOPMENT PROSPECTS OF THE ALMATY METRO / Ppt-Presentation by Gleb K.Samoilov. – Almaty, 2016. – 47 p. Основы мировой экономики. Демография
Основы мировой экономики. Демография Мугалимдин эң мыкты деңгээлде өсүп-өнүгүшү билим берүүнүн сапатын
Мугалимдин эң мыкты деңгээлде өсүп-өнүгүшү билим берүүнүн сапатын Формы международных экономических отношений
Формы международных экономических отношений Хозяйственная специализация государств, обусловленная природно-географическими факторами
Хозяйственная специализация государств, обусловленная природно-географическими факторами Задачи определения нижних границ цен и многоступенчатого расчета маржинальной прибыли
Задачи определения нижних границ цен и многоступенчатого расчета маржинальной прибыли Валютно-финансовая система Германии
Валютно-финансовая система Германии Экономико-экологический риск в легкой промышленности
Экономико-экологический риск в легкой промышленности Оценка результатов рейтинга-2018 деловыми ассоциациями
Оценка результатов рейтинга-2018 деловыми ассоциациями Прогнозирование в электроэнергетике
Прогнозирование в электроэнергетике Czym jest ekonomia?
Czym jest ekonomia? Деловая переписка. Язык и стиль
Деловая переписка. Язык и стиль Что такое хозяйство страны
Что такое хозяйство страны КАЙЗЕН. Ключ к экономическому успеху
КАЙЗЕН. Ключ к экономическому успеху Тарифное регулирование в сфере теплоснабжения на 2015 -2017 годы
Тарифное регулирование в сфере теплоснабжения на 2015 -2017 годы Издержки, понятия, виды
Издержки, понятия, виды Китайско-Казахстанская Ассоциация предпринимателей продовольственной индустрии
Китайско-Казахстанская Ассоциация предпринимателей продовольственной индустрии Процесс производства и его факторы. Практическое занятие 2
Процесс производства и его факторы. Практическое занятие 2 Теория фирмы
Теория фирмы Вступление России в ВТО: плюсы и минусы
Вступление России в ВТО: плюсы и минусы Контрольные вопросы
Контрольные вопросы Автоматизированная банковская система Подготовили Студентки группы МЭ091 Рудакова Татьяна, Еросова Валерия
Автоматизированная банковская система Подготовили Студентки группы МЭ091 Рудакова Татьяна, Еросова Валерия Факторы, влияющие на рынок нанотехнологии в России
Факторы, влияющие на рынок нанотехнологии в России