Содержание
- 2. Потоки минимальной стоимости Пусть h некоторый поток в сети Gf . Определим по h поток в
- 3. Потоки минимальной стоимости Лемма 2. Для любых двух допустимых потоков f и g в сети G
- 4. Потоки минимальной стоимости Удельной стоимостью пути (или цикла) в сети будем называть сумму удельных стоимостей входящих
- 5. Потоки минимальной стоимости Следствие 1. Нулевой поток в сети G тогда и только тогда имеет минимальную
- 6. Потоки минимальной стоимости Теорема 1 показывает, что алгоритм Басакера - Гоуэна имеет смысл применять только к
- 7. ИСО γ=2, S=10. [-3] 2
- 8. ИСО γ=3, S=16.
- 9. Потоки минимальной стоимости Алгоритм Клейна Его сущность заключается в том, что вначале нужно найти какой-нибудь поток
- 10. Потоки минимальной стоимости Пример. Построить поток величиной 5 с минимальной стоимостью в следующей сети: c 3[
- 12. Скачать презентацию
Слайд 2Потоки минимальной стоимости
Пусть h некоторый поток в сети Gf . Определим по
Потоки минимальной стоимости
Пусть h некоторый поток в сети Gf . Определим по

h поток в сети G по формуле
. Для любой вершины выполняется равенство Поэтому
- поток. Здесь .
Лемма 1. Пусть f - допустимый поток в сети G = (V,E) , h – допустимый поток в сети Gf =(Vf ,Ef) и
- определённый выше поток в сети G . Тогда поток допустим в G , причём
Доказательство. В силу допустимости потока h в сети Gf получим
Поэтому , что означает допустимость потока . Из равенства
вытекает Наконец
■
Для потоков f , g в сети G определим новый поток h=gѲf в сети Gf :
1) если и g(e) > f(e), то h(e) = g(e) – f(e);
2) если ;
3) на всех остальных дугах сети Gf поток считаем равным 0.
Очевидно gѲf всегда неотрицательна. Поэтому, вообще говоря gѲf ≠ fѲg . Более того, функции gѲf и fѲg определены на разных сетях Gf и Gg .
Отметим, что для любых допустимых потоков f и g в сети G и для любой вершины v из V
выполняется равенство div (gѲf) (v) = div (g-f) (v) .
. Для любой вершины выполняется равенство Поэтому
- поток. Здесь .
Лемма 1. Пусть f - допустимый поток в сети G = (V,E) , h – допустимый поток в сети Gf =(Vf ,Ef) и
- определённый выше поток в сети G . Тогда поток допустим в G , причём
Доказательство. В силу допустимости потока h в сети Gf получим
Поэтому , что означает допустимость потока . Из равенства
вытекает Наконец
■
Для потоков f , g в сети G определим новый поток h=gѲf в сети Gf :
1) если и g(e) > f(e), то h(e) = g(e) – f(e);
2) если ;
3) на всех остальных дугах сети Gf поток считаем равным 0.
Очевидно gѲf всегда неотрицательна. Поэтому, вообще говоря gѲf ≠ fѲg . Более того, функции gѲf и fѲg определены на разных сетях Gf и Gg .
Отметим, что для любых допустимых потоков f и g в сети G и для любой вершины v из V
выполняется равенство div (gѲf) (v) = div (g-f) (v) .
Слайд 3Потоки минимальной стоимости
Лемма 2. Для любых двух допустимых потоков f и g
Потоки минимальной стоимости
Лемма 2. Для любых двух допустимых потоков f и g

в сети G = (V,E) поток h = gѲf в сети Gf =(Vf ,Ef) также допустим. Для него справедливы равенства v(h) = v(g) – v(f) и S(h) = S(g) – S(f) .
Доказательство. Рассмотрим произвольную дугу е ∈ Е. В силу допустимости потоков f, g, если g(e) > f(e), то h(e) = g(e) - f(e) ≤ с(е) - f(е), а если g(e) < f(e), тo h(ē) = f(e) - g(e) ≤ f(e). Отсюда видно, что поток h допустим. Из div (gѲf) (v) = div (g-f) (v) вытекает, что мощность потока h равна
γ(g - f) = γ(g) - γ(f). Далее, из определения h следует, что для любой дуги е ∈ Е выполняется равенство (g(e) - f(e))d(e) = h(e)df(e)+h(ē)df(ē) (в правой части которого одно из слагаемых нулевое или вообще отсутствует). Поэтому S(h)= h(e')df(e')= (g(e) - f(e))d(e) =
= S(g - f)=S(g) - S(f). ■
Доказательство. Рассмотрим произвольную дугу е ∈ Е. В силу допустимости потоков f, g, если g(e) > f(e), то h(e) = g(e) - f(e) ≤ с(е) - f(е), а если g(e) < f(e), тo h(ē) = f(e) - g(e) ≤ f(e). Отсюда видно, что поток h допустим. Из div (gѲf) (v) = div (g-f) (v) вытекает, что мощность потока h равна
γ(g - f) = γ(g) - γ(f). Далее, из определения h следует, что для любой дуги е ∈ Е выполняется равенство (g(e) - f(e))d(e) = h(e)df(e)+h(ē)df(ē) (в правой части которого одно из слагаемых нулевое или вообще отсутствует). Поэтому S(h)= h(e')df(e')= (g(e) - f(e))d(e) =
= S(g - f)=S(g) - S(f). ■
Слайд 4Потоки минимальной стоимости
Удельной стоимостью пути (или цикла) в сети будем называть сумму
Потоки минимальной стоимости
Удельной стоимостью пути (или цикла) в сети будем называть сумму

удельных стоимостей входящих в него дуг.
Теорема 1. (Критерий оптимальности потока фиксированной мощности). Пусть дана сеть G с заданными пропускными способностями и удельными стоимостями дуг, источником s и стоком t. Тогда допустимый поток f в сети G имеет минимальную стоимость среди всех допустимых потоков той же величины в том и только том случае, когда в графе Gf нет контуров с отрицательной удельной стоимостью.
Доказательство. Пусть f – поток величины m с минимальной стоимостью. Предположим, что в графе Gf есть контур с отрицательной удельной стоимостью. Обозначим через ρ минимальную пропускную способность дуг этого контура. Число ρ положительно. Пропустим по контуру поток h, который принимает значение ρ на всех дугах контура и нулевое значение на остальных дугах. Легко видеть, что этот поток допустим в сети Gf , имеет отрицательную стоимость, а его величина равна нулю. Ему соответствует поток в сети G. По лемме 1 поток f + допустим, имеет величину v(f), а его стоимость строго меньше S(f). Значит, стоимость потока f не минимальна.
С другой стороны, допустим, что поток f не оптимален. Тогда существует такой допустимый поток g в сети G, что γ(g) = γ(f), a S(g)
Теорема 1. (Критерий оптимальности потока фиксированной мощности). Пусть дана сеть G с заданными пропускными способностями и удельными стоимостями дуг, источником s и стоком t. Тогда допустимый поток f в сети G имеет минимальную стоимость среди всех допустимых потоков той же величины в том и только том случае, когда в графе Gf нет контуров с отрицательной удельной стоимостью.
Доказательство. Пусть f – поток величины m с минимальной стоимостью. Предположим, что в графе Gf есть контур с отрицательной удельной стоимостью. Обозначим через ρ минимальную пропускную способность дуг этого контура. Число ρ положительно. Пропустим по контуру поток h, который принимает значение ρ на всех дугах контура и нулевое значение на остальных дугах. Легко видеть, что этот поток допустим в сети Gf , имеет отрицательную стоимость, а его величина равна нулю. Ему соответствует поток в сети G. По лемме 1 поток f + допустим, имеет величину v(f), а его стоимость строго меньше S(f). Значит, стоимость потока f не минимальна.
С другой стороны, допустим, что поток f не оптимален. Тогда существует такой допустимый поток g в сети G, что γ(g) = γ(f), a S(g)
Слайд 5Потоки минимальной стоимости
Следствие 1. Нулевой поток в сети G тогда и только
Потоки минимальной стоимости
Следствие 1. Нулевой поток в сети G тогда и только

тогда имеет минимальную стоимость среди всех допустимых потоков нулевой величины, когда в G нет контура с отрицательной удельной стоимостью.
Следствие 2. Допустимый поток f в сети G имеет минимальную стоимость среди всех допустимых потоков той же величины в том и только том случае, когда не существует потока h вдоль неориентированного цикла в сети G, который удовлетворял бы следующим двум условиям: а) поток f + h допустим и б) S(h) < 0.
Алгоритм Басакера − Гоуэна
На каждом его шаге находится наиболее дешевый ориентированный путь из s в t в графе модифицированных стоимостей Gf. По леммам 1, 2 этому пути соответствует увеличивающая цепь минимальной удельной стоимости в сети G. Затем по этой цепи пропускается максимальный поток, который можно добавить к имеющемуся потоку f .
Шаг 0. В сети G пропускаем нулевой поток f. Его величина и стоимость равны нулю.
Шаг 1. Строим граф модифицированных стоимостей Gf.
Шаг 2. Если в Gf нет ни одного ориентированного пути из s в t, то мощность потока f не может быть увеличена, и задача не имеет решения. В противном случае среди всех путей из s в t в графе Gf находим путь с минимальной удельной стоимостью. Обозначим его Pf.
Шаг 3. В исходной сети G определяем неориентированную цепь Р, соответствующую пути Pf. Для всех дуг е из цепи Р вычисляем числа ρ(е): на прямых дугах ρ(е) = с(е) - f(e), а на обратных дугах ρ(е) = f(е). Затем находим ρ = min{ρ(e), m - v(f)| е∈ P}. На прямых дугах цепи Р увеличиваем поток f на ρ, а на обратных дугах уменьшаем поток f на ρ. При этом величина потока увеличивается на ρ.
Шаг 4. Если величина нового потока меньше т, то переходим к шагу 1. Если же она равна т, то в сети построен оптимальный поток мощности т.
Следствие 2. Допустимый поток f в сети G имеет минимальную стоимость среди всех допустимых потоков той же величины в том и только том случае, когда не существует потока h вдоль неориентированного цикла в сети G, который удовлетворял бы следующим двум условиям: а) поток f + h допустим и б) S(h) < 0.
Алгоритм Басакера − Гоуэна
На каждом его шаге находится наиболее дешевый ориентированный путь из s в t в графе модифицированных стоимостей Gf. По леммам 1, 2 этому пути соответствует увеличивающая цепь минимальной удельной стоимости в сети G. Затем по этой цепи пропускается максимальный поток, который можно добавить к имеющемуся потоку f .
Шаг 0. В сети G пропускаем нулевой поток f. Его величина и стоимость равны нулю.
Шаг 1. Строим граф модифицированных стоимостей Gf.
Шаг 2. Если в Gf нет ни одного ориентированного пути из s в t, то мощность потока f не может быть увеличена, и задача не имеет решения. В противном случае среди всех путей из s в t в графе Gf находим путь с минимальной удельной стоимостью. Обозначим его Pf.
Шаг 3. В исходной сети G определяем неориентированную цепь Р, соответствующую пути Pf. Для всех дуг е из цепи Р вычисляем числа ρ(е): на прямых дугах ρ(е) = с(е) - f(e), а на обратных дугах ρ(е) = f(е). Затем находим ρ = min{ρ(e), m - v(f)| е∈ P}. На прямых дугах цепи Р увеличиваем поток f на ρ, а на обратных дугах уменьшаем поток f на ρ. При этом величина потока увеличивается на ρ.
Шаг 4. Если величина нового потока меньше т, то переходим к шагу 1. Если же она равна т, то в сети построен оптимальный поток мощности т.
Слайд 6Потоки минимальной стоимости
Теорема 1 показывает, что алгоритм Басакера - Гоуэна имеет смысл
Потоки минимальной стоимости
Теорема 1 показывает, что алгоритм Басакера - Гоуэна имеет смысл
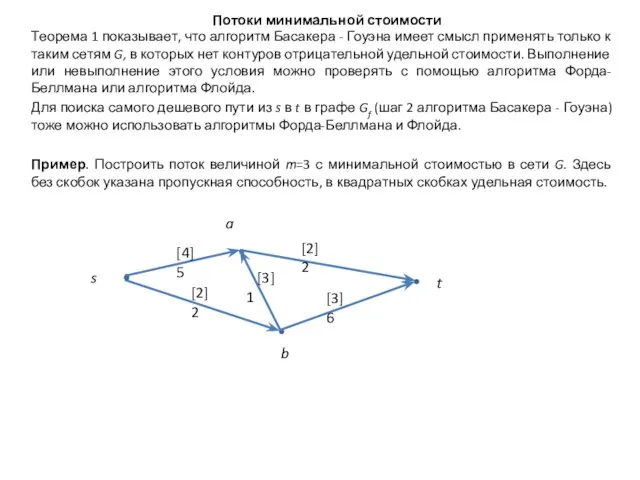
применять только к таким сетям G, в которых нет контуров отрицательной удельной стоимости. Выполнение или невыполнение этого условия можно проверять с помощью алгоритма Форда-Беллмана или алгоритма Флойда.
Для поиска самого дешевого пути из s в t в графе Gf (шаг 2 алгоритма Басакера - Гоуэна) тоже можно использовать алгоритмы Форда-Беллмана и Флойда.
Пример. Построить поток величиной m=3 с минимальной стоимостью в сети G. Здесь без скобок указана пропускная способность, в квадратных скобках удельная стоимость.
Для поиска самого дешевого пути из s в t в графе Gf (шаг 2 алгоритма Басакера - Гоуэна) тоже можно использовать алгоритмы Форда-Беллмана и Флойда.
Пример. Построить поток величиной m=3 с минимальной стоимостью в сети G. Здесь без скобок указана пропускная способность, в квадратных скобках удельная стоимость.
Слайд 7ИСО
γ=2, S=10.
[-3]
2
ИСО
γ=2, S=10.
[-3]
2
![ИСО γ=2, S=10. [-3] 2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/885252/slide-6.jpg)
Слайд 8ИСО
γ=3, S=16.
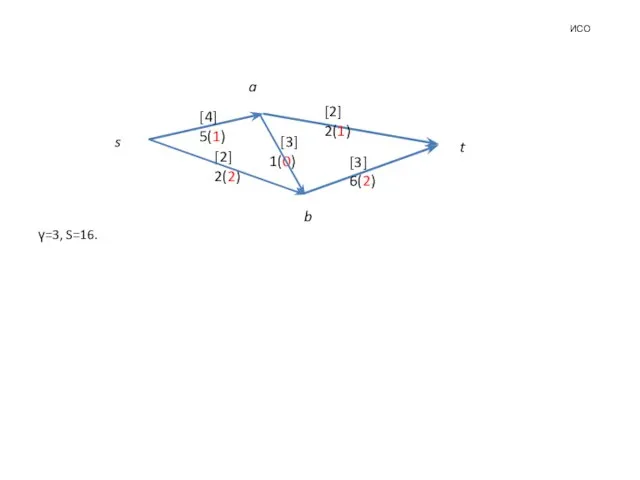
ИСО
γ=3, S=16.
Слайд 9Потоки минимальной стоимости
Алгоритм Клейна
Его сущность заключается в том, что вначале нужно найти
Потоки минимальной стоимости
Алгоритм Клейна
Его сущность заключается в том, что вначале нужно найти

какой-нибудь поток f величины т, а затем последовательно уменьшать его стоимость, перестраивая вдоль имеющихся циклов с отрицательной удельной стоимостью. При этих перестройках величина потока f будет сохраняться. В тот момент, когда циклы с отрицательной удельной стоимостью исчезнут, поток f станет оптимальным.
Шаг 0. Находим любой допустимый поток f величины γ (f) = т .
Это можно сделать с помощью алгоритма Форда-Фалкерсона (в котором вычисления нужно проводить до тех пор, пока поток не достигнет величины т). Если в сети не существует допустимого потока величины т, то задача не имеет решения.
Шаг 1. Строим граф модифицированных стоимостей Gf . Если в нем нет контуров с отрицательной удельной стоимостью, то задача решена: построенный поток f имеет минимальную стоимость среди потоков величины т. В противном случае находим в графе Gf контур Рf с отрицательной удельной стоимостью (например, с помощью алгоритма Флойда).
Шаг 2. В исходной сети G определяем неориентированный цикл Р, соответствующий контуру Рf. Все дуги е∈Р разбиваются на два класса: прямые, для которых е∈Рf, и обратные, для которых ē∈Pf - (где ē - дуга, противоположная е). Вычисляем ρ = min{p(e)| е∈ P}, где ρ (е ) = с (е) - f (е ) на прямых дугах и ρ (е ) = f (е) на обратных дугах.
Шаг 3. На прямых дугах цикла Р увеличиваем поток f на ρ, а на обратных дугах цикла Р уменьшаем поток f на ρ. Переходим к шагу 1.
Шаг 0. Находим любой допустимый поток f величины γ (f) = т .
Это можно сделать с помощью алгоритма Форда-Фалкерсона (в котором вычисления нужно проводить до тех пор, пока поток не достигнет величины т). Если в сети не существует допустимого потока величины т, то задача не имеет решения.
Шаг 1. Строим граф модифицированных стоимостей Gf . Если в нем нет контуров с отрицательной удельной стоимостью, то задача решена: построенный поток f имеет минимальную стоимость среди потоков величины т. В противном случае находим в графе Gf контур Рf с отрицательной удельной стоимостью (например, с помощью алгоритма Флойда).
Шаг 2. В исходной сети G определяем неориентированный цикл Р, соответствующий контуру Рf. Все дуги е∈Р разбиваются на два класса: прямые, для которых е∈Рf, и обратные, для которых ē∈Pf - (где ē - дуга, противоположная е). Вычисляем ρ = min{p(e)| е∈ P}, где ρ (е ) = с (е) - f (е ) на прямых дугах и ρ (е ) = f (е) на обратных дугах.
Шаг 3. На прямых дугах цикла Р увеличиваем поток f на ρ, а на обратных дугах цикла Р уменьшаем поток f на ρ. Переходим к шагу 1.
Слайд 10Потоки минимальной стоимости
Пример. Построить поток величиной 5 с минимальной стоимостью в следующей
Потоки минимальной стоимости
Пример. Построить поток величиной 5 с минимальной стоимостью в следующей
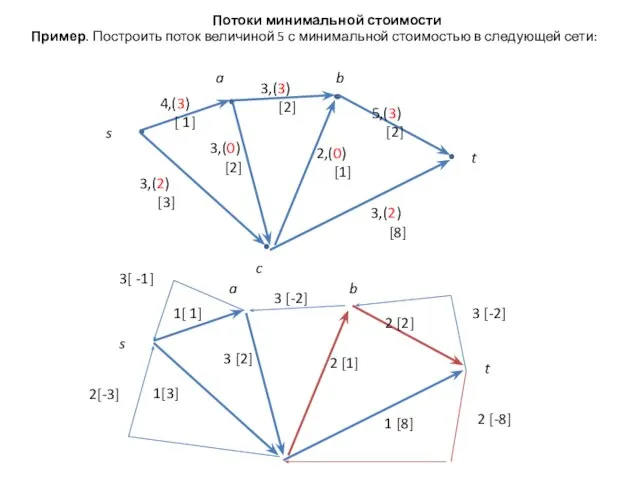
сети:
c
3[ -1]
2[-3]
2 [-8]
3 [-2]
- Предыдущая
ГИС_Введение_Лекция 6 (1)Следующая -
Уральский экономический район Экономика. 11 фм. класс
Экономика. 11 фм. класс Характеристика экономики Архангельской области 2016-2017 гг
Характеристика экономики Архангельской области 2016-2017 гг Совершенствование и развитие теории экономической науки и менеджмента
Совершенствование и развитие теории экономической науки и менеджмента Кривая производственных возможностей
Кривая производственных возможностей Экономические аспекты инфокоммуникаций
Экономические аспекты инфокоммуникаций Современный глобальный кредитный кризис
Современный глобальный кредитный кризис Окупаемость инвестиций ROI
Окупаемость инвестиций ROI Современный этап мирового развития. Урок 99-100. Глобализация и её последствия
Современный этап мирового развития. Урок 99-100. Глобализация и её последствия World environmental organizations
World environmental organizations Экономика_организации_Ресурсы_организации
Экономика_организации_Ресурсы_организации Падающая звезда
Падающая звезда Трудовые ресурсы
Трудовые ресурсы Identification de marché et analyse swot
Identification de marché et analyse swot Государственное регулирование в НГК
Государственное регулирование в НГК Инфляция
Инфляция Доходы предприятий
Доходы предприятий Рынок как форма
Рынок как форма Факторы производства
Факторы производства Розрахунок штату РТД
Розрахунок штату РТД Экономика. Рынок. Кредиты
Экономика. Рынок. Кредиты Энергосбережение при грануляции шлаков
Энергосбережение при грануляции шлаков Экономический кризис (экономические и промышленно-финансовые потрясения)
Экономический кризис (экономические и промышленно-финансовые потрясения) Безработица
Безработица Expert, analytical and control activities in the area of federal budget expenditures
Expert, analytical and control activities in the area of federal budget expenditures Экономика приусадебного участка
Экономика приусадебного участка Концепция установления прожиточного минимума и минимального размера оплаты труда
Концепция установления прожиточного минимума и минимального размера оплаты труда Потребности. Ограниченность ресурсов
Потребности. Ограниченность ресурсов Прожиточный минимум, потребительская корзина
Прожиточный минимум, потребительская корзина