Приложение определенного интеграла в экономике

1
Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией f(t) = 3/(3t +1) + 4.

РЕШЕНИЕ
Если f(t) характеризует производительность труда рабочего в зависимости от (времени) t, то объем продукции, за времени от t1 до t2 будет выражаться формулой:
В нашем случае:
=
= ln10/7 + 4
V
=ln10
+ 12
– ln7
– 8

2
Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией f(t) = 2t + 5.

РЕШЕНИЕ
Имеем:
V
+ 5t)
= 9
+15
=24
=
=
- 0 - 0

Задачи на определение излишка потребителя.

3
Известно, что спрос на некоторый товар задается функцией p=4–q2, где q–количество товара (в шт.), p– цена единицы товара (в руб.), а равновесие на рынке данного товара достигается при p*=q*=1. Определите величину потребительского излишка.

РЕШЕНИЕ

4

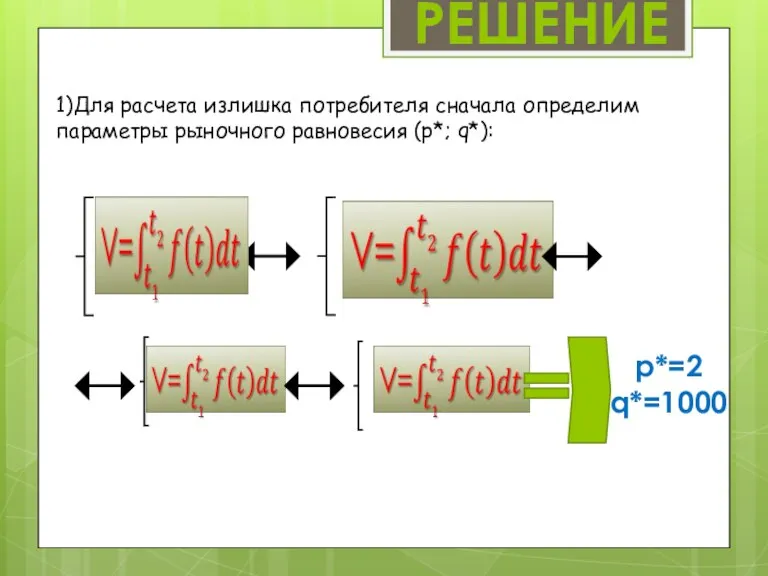
РЕШЕНИЕ
1)Для расчета излишка потребителя сначала определим параметры рыночного равновесия (p*; q*):
p*=2
q*=1000

2)Формула для вычисления потребительского излишка:
f(q)-обратная

5

РЕШЕНИЕ
1)Выигрыш потребителя это потребительский излишек. Для того, чтобы найти его, определим равновесные значения количества товара и его цены:

2)Посчитаем потребительский излишек:

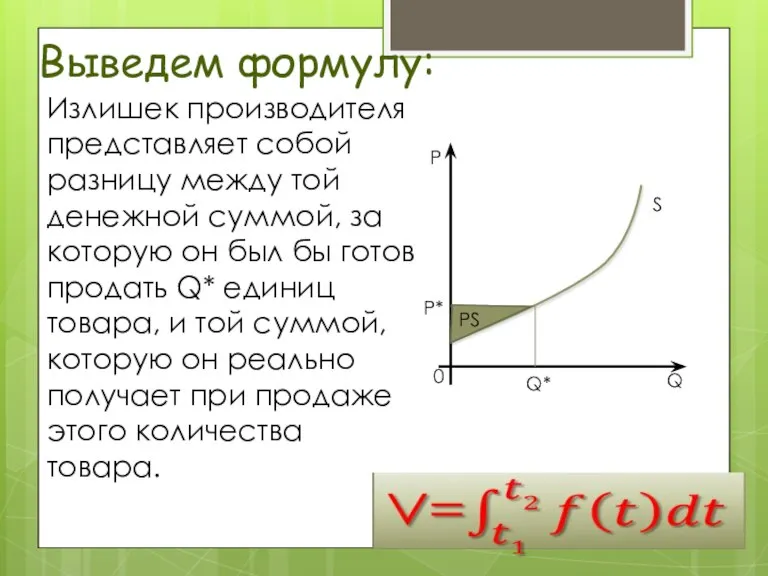
Излишек производителя представляет собой разницу между той денежной суммой, за которую он был бы готов продать Q* единиц товара, и той суммой, которую он реально получает при продаже этого количества товара.
Выведем формулу:
P
S
Q
Q*
P*
0
PS

6
Известно, что кривая предложения некоторого товара имеет вид p = 4q3 + 2, а равновесие на рынке данного товара достигается при объеме продаж Q* = 3. Определите добавочную выгоду производителя при продаже такого количества продукции.

РЕШЕНИЕ
1)Найдем равновесное значение цены:
=110
2) Подставим полученное значение в формулу:

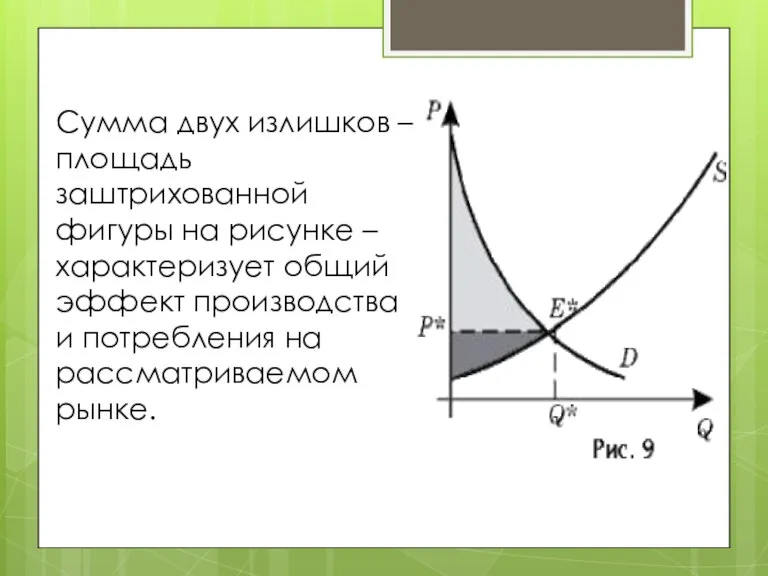
Cумма двух излишков – площадь заштрихованной фигуры на рисунке – характеризует общий эффект производства и потребления на рассматриваемом рынке.

7

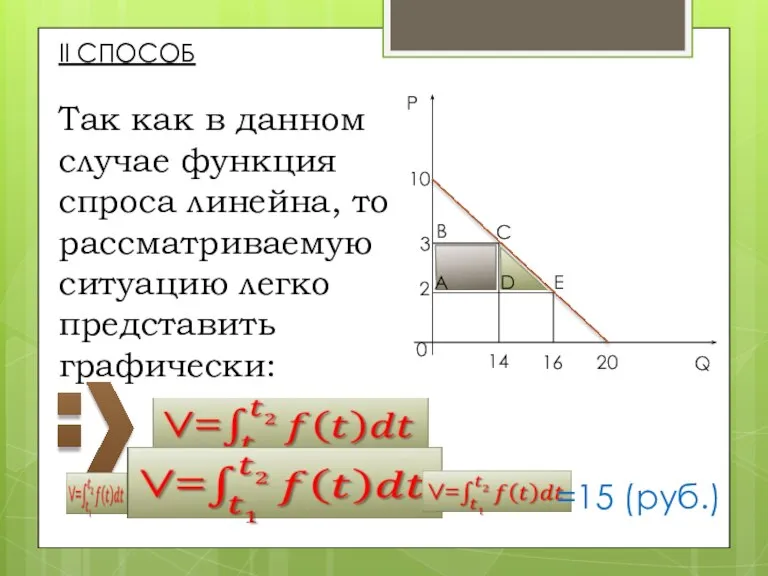
РЕШЕНИЕ
I СПОСОБ
Для определения потребительских потерь при увеличении равновесной цены товара с 2 руб. до 3 руб. посмотрим, как при этом меняется объем продаж:

=15 (руб.)

II СПОСОБ
Так как в данном случае функция спроса линейна, то рассматриваемую ситуацию легко представить графически:
C
14
16
20
Q
E
D
A
B
3
2
0
10
P
=15 (руб.)

8
Найти объем продукции, произведенной за 4 года, если функция Кобба - Дугласа имеет вид: z(t) = (1 + t)∙ e3t.

РЕШЕНИЕ

9

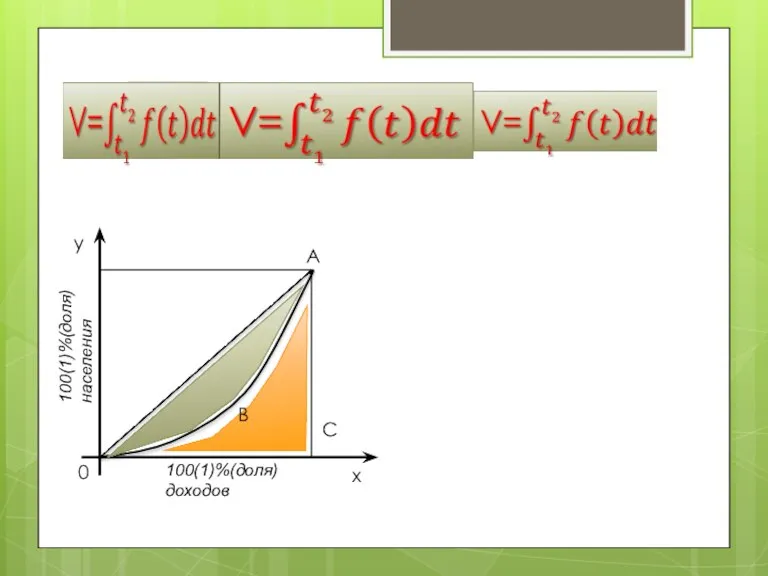
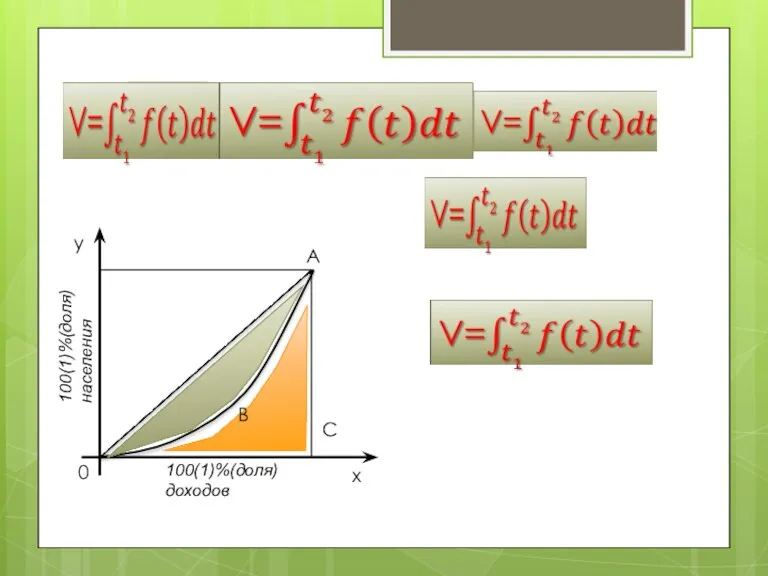
РЕШЕНИЕ
Для анализа социально - экономического строения общества используется так называемая «кривая Джинни» (или «кривая Лоренца») распределения богатства в обществе.
При равномерном распределении доходов кривая Джинни выражается в прямую - биссектрису ОА, поэтому площадь фигуры ОАВ между биссектрисой ОА и кривой Джинни, отнесенная к площади треугольника ОАС (коэффициент Джинни), характеризует степень неравенства в распределении доходов населения.

A
x
C
B
0
y
100(1)%(доля) доходов
100(1)%(доля) населения

A
x
C
B
0
y
100(1)%(доля) доходов
100(1)%(доля) населения

10
Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10млрд. руб. и намечается ежегодно увеличивать капиталовложения на 1млрд. руб.

РЕШЕНИЕ
Капиталовложения задаются функцией: f (х) = 10 + 1· t = 10+ t
Удельная процентная ставка i=0,08