Содержание
- 2. Задача классификации Задача классификации Области применения алгоритмов классификации Формальное математическое определение Несбалансированная классификация Критерии качества классификации:
- 3. Области применения алгоритмов классификации
- 4. Области применения алгоритмов классификации Регрессия - множество ответов бесконечно, так как они являются действительными числами или
- 5. Области применения алгоритмов классификации Оценка кредитоспособности заемщиков. Задачи медицинской диагностики Оптическое распознавание символов. Распознавание речи. Обнаружение
- 6. Формальное математическое определение
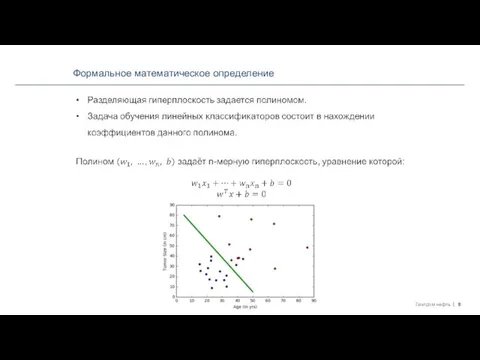
- 7. Формальное математическое определение Разделяющая гиперплоскость – это гиперплоскость, которая отделяет группы объектов, принадлежащим различным классам. Если
- 8. Формальное математическое определение
- 9. Формальное математическое определение
- 10. Несбалансированная классификация Imbalanced Data : один из классов представлен значительно бо́льшим количеством объектов, чем другой –
- 11. Несбалансированная классификация Задачи, в которых несбалансированность данных не просто общая проблема, а ожидаема в силу специфики
- 12. Несбалансированная классификация Обучение на несбалансированных данных осложняется расположением отдельных примеров выборок: Вкрапления Наложения s – чистые
- 13. Несбалансированная классификация Основные подходы к решению проблемы несбалансированных данных в классификации: Сэмплинг (sampling) Уменьшение большего класса
- 14. Несбалансированная классификация Уменьшение большего класса (Undersampling) Случайный или синтетический выбор прецедентов мажоритарного класса в обучающую выборку.
- 15. Несбалансированная классификация Уменьшение большего класса (Undersampling) Поиск связей Томека (Tomek Links) Этот способ хорошо удаляет записи,
- 16. Несбалансированная классификация Уменьшение большего класса (Undersampling) Правило сосредоточенного ближайшего соседа (Condensed Nearest Neighbor Rule) Этот метод
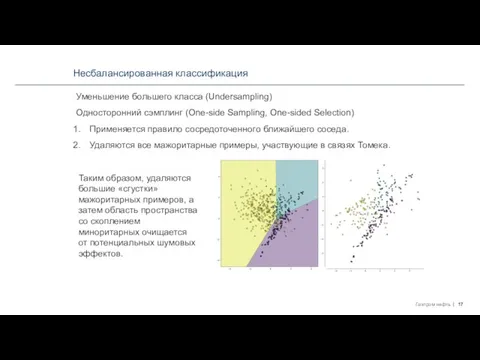
- 17. Несбалансированная классификация Уменьшение большего класса (Undersampling) Односторонний сэмплинг (One-side Sampling, One-sided Selection) Применяется правило сосредоточенного ближайшего
- 18. Несбалансированная классификация Уменьшение большего класса (Undersampling) Правило «очищающего» соседа (Neighborhood Cleaning Rule) Все примеры классифицируются по
- 19. Несбалансированная классификация Увеличение меньшего класса (Oversampling) Добавление прецедентов миноритарного класса позволяет сохранить всю имеющуюся информацию. Недостаток
- 20. Несбалансированная классификация Увеличение меньшего класса (Oversampling) Алгоритм SMOTE (Synthetic Minority Oversampling Technique) - генерация некоторого количества
- 21. Несбалансированная классификация Увеличение меньшего класса (Oversampling) Алгоритм ADASYN (Adaptive Synthetic Minority Oversampling) - использование функции плотности
- 22. Несбалансированная классификация Изменение порога решения (Changing Performance Metric) Многие алгоритмы классификации определяют степень достоверности предсказания. При
- 23. Критерии качества классификации Определим ROC-кривую (receiver operating characteristic, рабочая характеристика приёмника) Ось абсцисс: доля неправильных положительных
- 24. Критерии качества классификации Точность и полнота (Precision and Recall) для случая бинарной классификации TP - правильные
- 25. Критерии качества классификации
- 27. Скачать презентацию






















 Модели экономического роста. Экономика
Модели экономического роста. Экономика Типы экономических систем. Рынок
Типы экономических систем. Рынок Золото в экономике
Золото в экономике Занимательный урок экономики География в купюрах России
Занимательный урок экономики География в купюрах России Международные валютно-финансовые отношения. Характеристики финансовой системы. Типы валютных курсов. (Тема 16)
Международные валютно-финансовые отношения. Характеристики финансовой системы. Типы валютных курсов. (Тема 16) Расчет экспортной, импортной и внешнеторговой квоты за период с 2000 по 2012 года на примере Новой Зеландии и ЮАР Подготовили: Сакович
Расчет экспортной, импортной и внешнеторговой квоты за период с 2000 по 2012 года на примере Новой Зеландии и ЮАР Подготовили: Сакович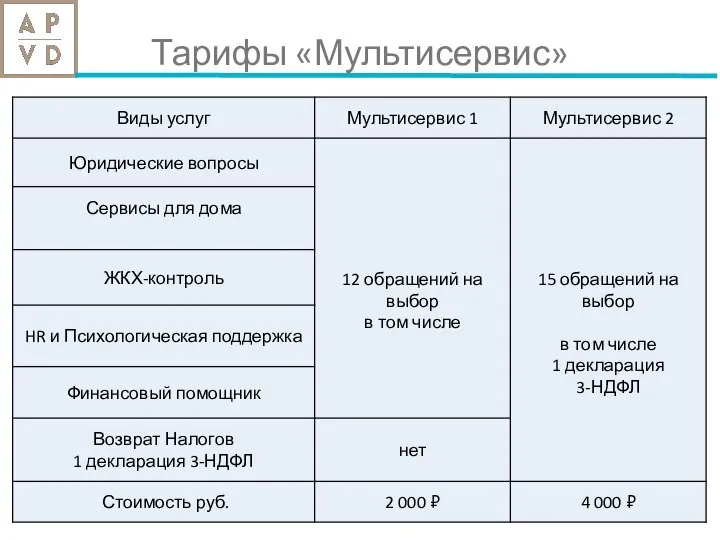 Тарифы Мультисервис
Тарифы Мультисервис Модели пространственного размещения
Модели пространственного размещения Характерные признаки государственных программ
Характерные признаки государственных программ Экономика Л-19 КР
Экономика Л-19 КР Формы организаций
Формы организаций Культурные факторы регионализации
Культурные факторы регионализации Экономическое развитие России: роль несырьевого сектора
Экономическое развитие России: роль несырьевого сектора International Humor Ambulance
International Humor Ambulance Экспорт порталини ишлаб чиқиш бўйича таклиф
Экспорт порталини ишлаб чиқиш бўйича таклиф Эволюция валютных систем Выполнила: Гафарова Сабира, группа Э091
Эволюция валютных систем Выполнила: Гафарова Сабира, группа Э091 Рыночный механизм
Рыночный механизм Славгородский таможенный пост, как место пересечения торговых путей из Казахстана в Сибирь
Славгородский таможенный пост, как место пересечения торговых путей из Казахстана в Сибирь Приложение определенного интеграла в экономике
Приложение определенного интеграла в экономике Функция с постоянной эластичностью замены между факторами
Функция с постоянной эластичностью замены между факторами Инвестиционные мегапроекты
Инвестиционные мегапроекты Основные фонды предприятия
Основные фонды предприятия Экономика: сессия синхронизации
Экономика: сессия синхронизации SWOT – анализ ОАО «Холод»
SWOT – анализ ОАО «Холод» Производственный и технологический процессы
Производственный и технологический процессы Оценочная деятельность в РФ
Оценочная деятельность в РФ Организация современного производства “АвтоВаз”
Организация современного производства “АвтоВаз”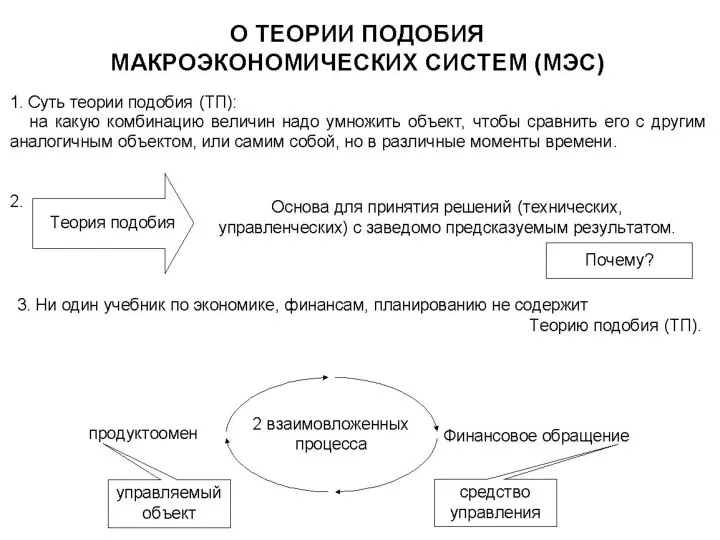 О теории подобия макроэкономических систем
О теории подобия макроэкономических систем