Содержание
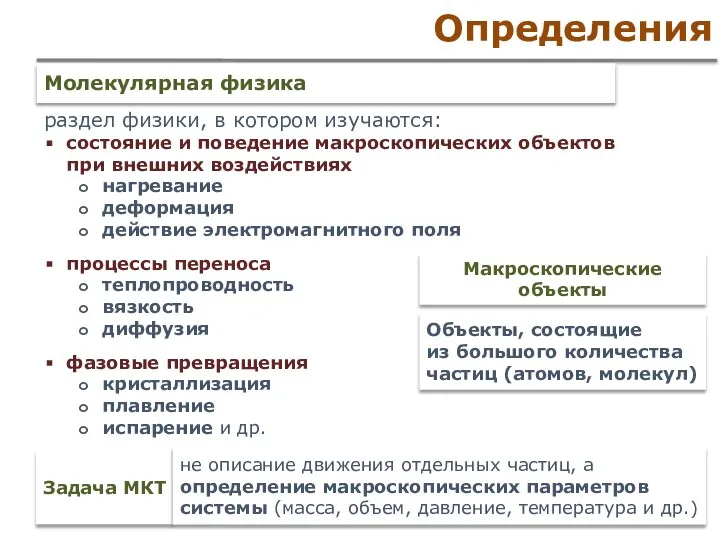
- 2. Определения раздел физики, в котором изучаются: состояние и поведение макроскопических объектов при внешних воздействиях нагревание деформация
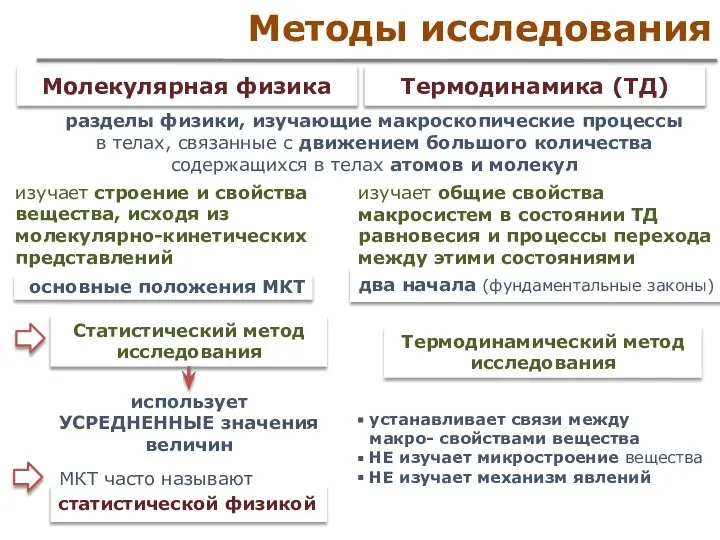
- 3. Методы исследования Термодинамический метод исследования Статистический метод исследования разделы физики, изучающие макроскопические процессы в телах, связанные
- 4. Атомно-молекулярное строение вещества Атомы и молекулы хаотически движутся Доказательство существования теплового хаотического движения молекул Физическое тело
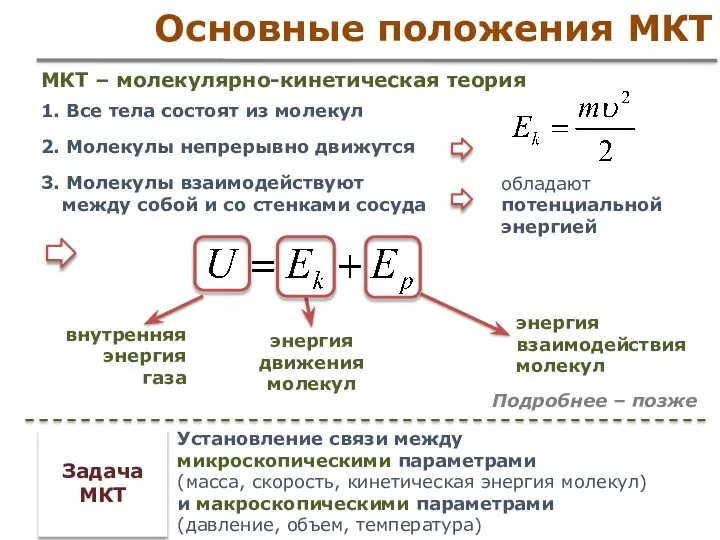
- 5. Основные положения МКТ 1. Все тела состоят из молекул 2. Молекулы непрерывно движутся 3. Молекулы взаимодействуют
- 6. Основные понятия Количество вещества число Авогадро При нормальных условиях (t=00С, P=105Па) моль любого газа занимает объем
- 7. Основные понятия Идеальный газ Размеры атомов (молекул) – пренебрежимо малы Силы межмолекулярного взаимодействия отсутствуют Взаимодействия –
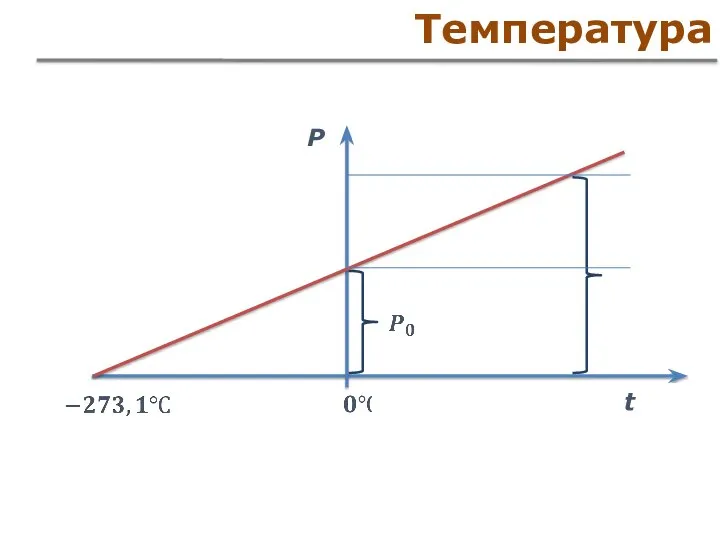
- 8. Основные параметры абсолютный нуль температуры – точка нулевого давления газа Реперные точки температура тройной точки воды:
- 9. Температура P t
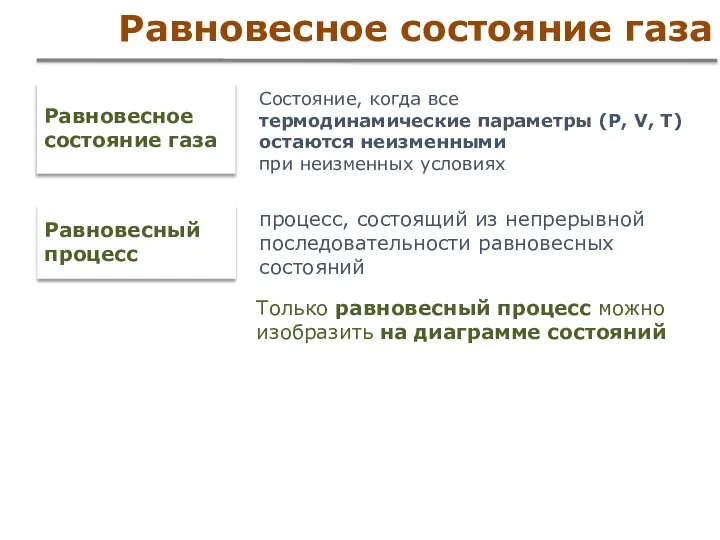
- 10. Равновесное состояние газа Равновесное состояние газа Состояние, когда все термодинамические параметры (Р, V, T) остаются неизменными
- 11. Законы, установленные опытным путем Закон Гей-Люссака (1802) Изобарный (изобарический) процесс Закон Шарля (1787) Изохорный (изохорический) процесс
- 12. Роберт Бойль и Эдм Мариотт Аббат, физик Robert Boyle 1627-1691, Англия 1620-1684, Франция Англо-ирландский натурфилософ, философ,
- 13. Жозеф Луи Гей-Люссак Французский физик и химик, ученик К.Л.Бертолле Открыл закон объемных отношений при реакциях между
- 14. Жак Александр Сезар Шарль Изобретатель наполняемого водородом, или другим газом легче воздуха, воздушного шара, получившего по
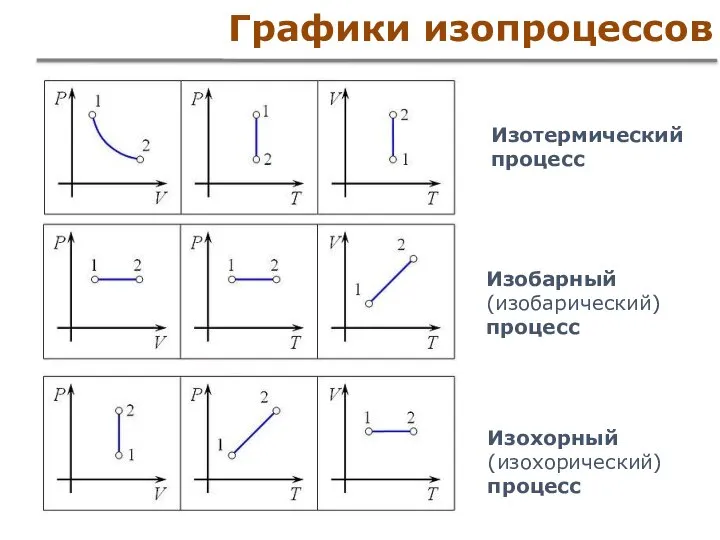
- 15. Графики изопроцессов Изобарный (изобарический) процесс Изохорный (изохорический) процесс Изотермический процесс
- 16. Уравнение состояния идеального газа при нормальных условиях: 1 моль газа занимает один и тот же объем
- 17. Дмитрий Иванович Менделеев Великий русский ученый-энциклопедист – сферы научных интересов: Химия Физика Физическая химия Метрология Экономика
- 18. Бенуа Поль Эмиль Клапейрон Французский физик и инженер Учился в парижской политехнической школе Был профессором в
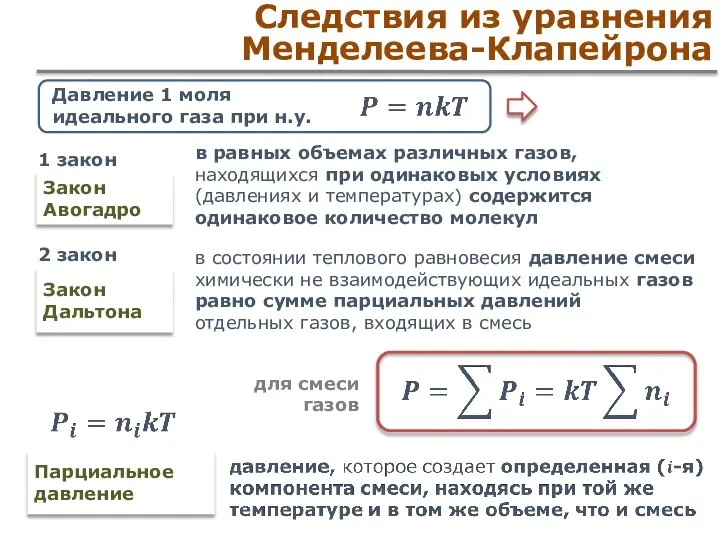
- 19. Следствия из уравнения Менделеева-Клапейрона Закон Авогадро в равных объемах различных газов, находящихся при одинаковых условиях (давлениях
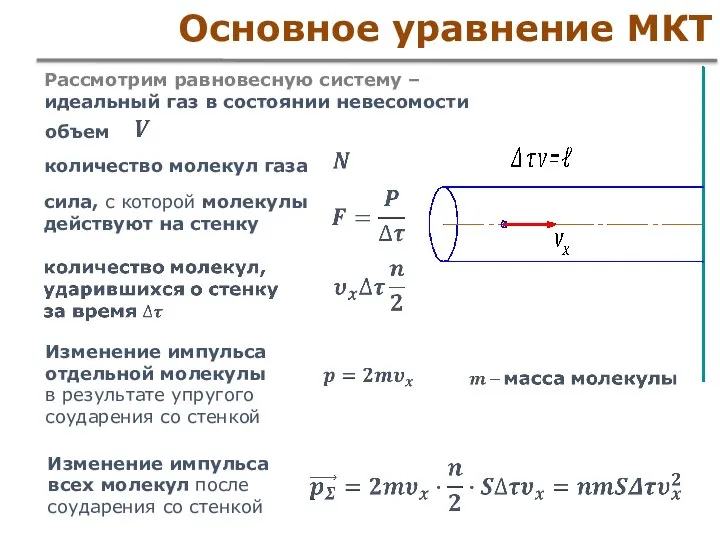
- 20. Основное уравнение МКТ Рассмотрим равновесную систему – идеальный газ в состоянии невесомости объем количество молекул газа
- 21. Основное уравнение МКТ Давление, оказываемое молекулами на стенку Направления движения каждой молекулы равноправны Скорости молекул различны
- 22. Основное уравнение МКТ Давление, оказываемое молекулами на стенку Направления движения каждой молекулы равноправны Скорости молекул различны
- 23. Взаимосвязь кинетической энергии и температуры средняя кинетическая энергия поступательного движения молекул идеального газа пропорциональна температуре Основное
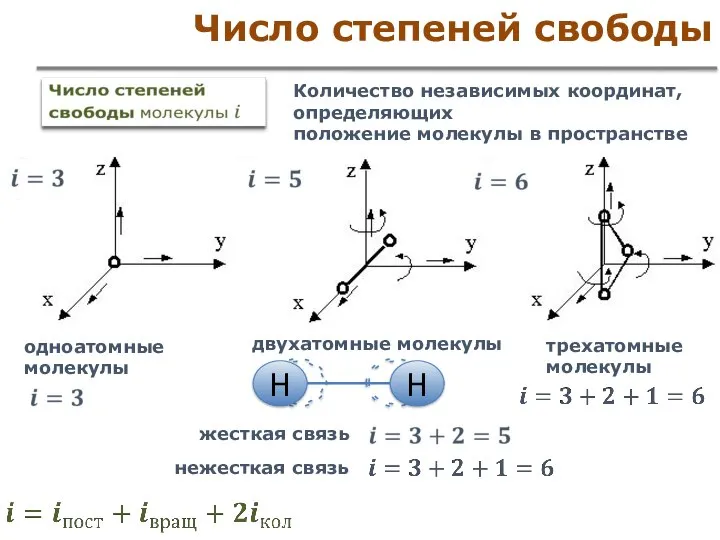
- 24. Число степеней свободы Количество независимых координат, определяющих положение молекулы в пространстве одноатомные молекулы двухатомные молекулы жесткая
- 25. Распределение тепловой энергии по степеням свободы молекул Число степеней свободы поступательного движения молекулы Средняя энергия поступательного
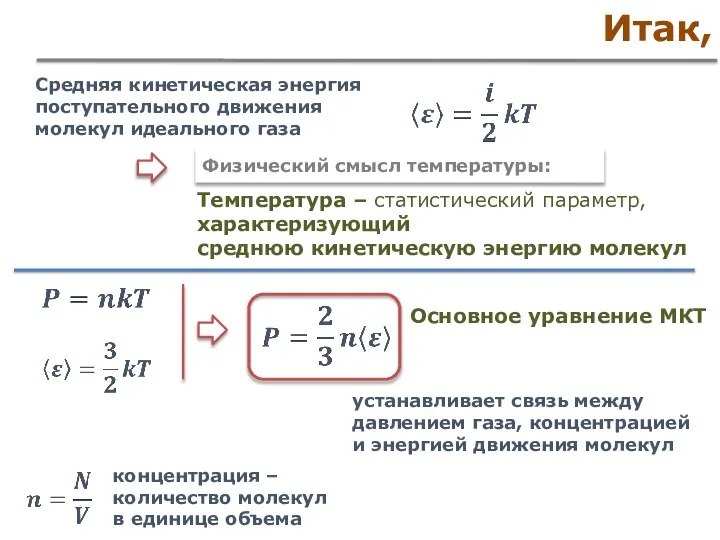
- 26. Итак, Средняя кинетическая энергия поступательного движения молекул идеального газа Физический смысл температуры: Температура – статистический параметр,
- 27. Элементы статистической физики: некоторые понятия Термодинамическая вероятность количество способов, которыми может быть реализовано данное состояние макросистемы
- 28. Элементы статистической физики Закон распределения молекул идеального газа по скоростям Статистическая функция распределения по скоростям Доска
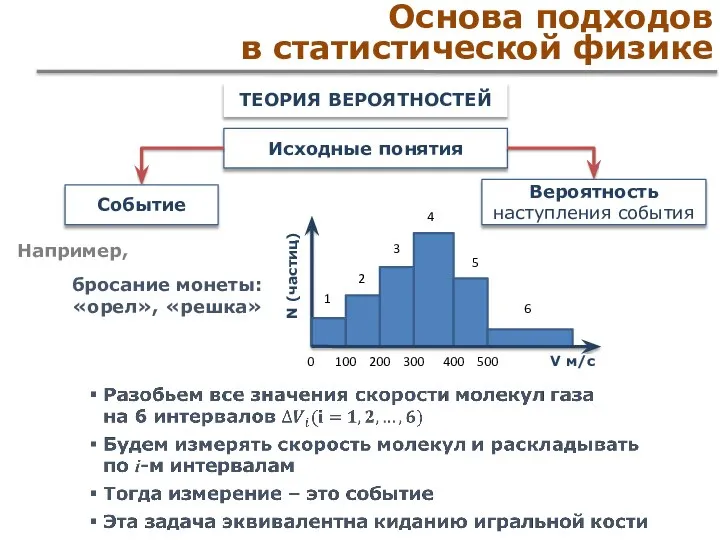
- 29. Основа подходов в статистической физике ТЕОРИЯ ВЕРОЯТНОСТЕЙ Исходные понятия Событие Вероятность наступления события Например, бросание монеты:
- 30. Основа подходов в статистической физике Событие случайное – условия его наступления неизвестны Вероятность повторения данного события
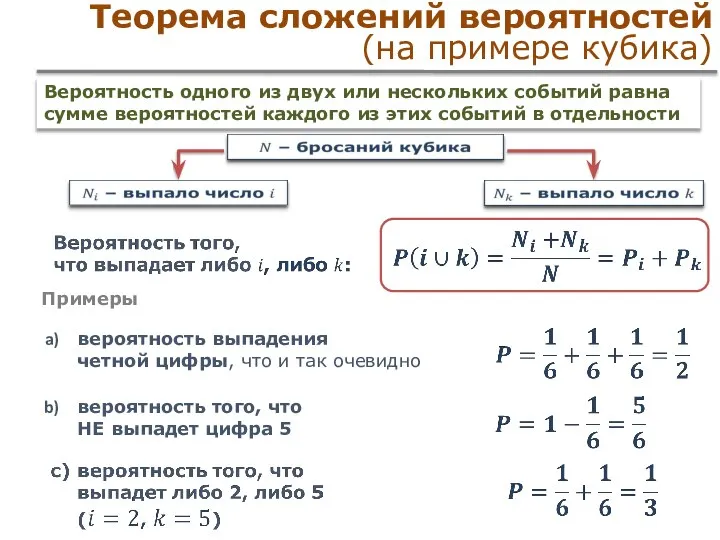
- 31. Теорема сложений вероятностей (на примере кубика) Примеры вероятность выпадения четной цифры, что и так очевидно вероятность
- 32. Теорема умножений вероятностей Вероятность совмещения двух или нескольких событий равна произведению вероятностей каждого из них в
- 33. Распределение вероятности события Характеристика случайной величины Функция распределения случайной величины Вероятность достоверного события:
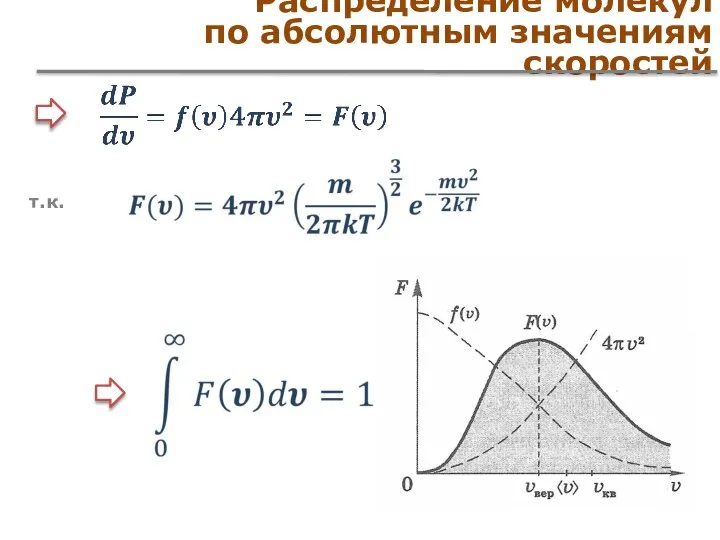
- 34. Распределение молекул по абсолютным значениям скоростей Фазовое пространство скоростей – фазовый объем – вероятность обнаружения молекулы
- 35. Распределение молекул по абсолютным значениям скоростей – функция распределения подробнее Для получения распределения запишем в общем
- 36. Распределение молекул по абсолютным значениям скоростей Вероятность того, что частица имеет проекцию скорости в интервале используя
- 37. Распределение молекул по абсолютным значениям скоростей – частицы, модуль скорости которых лежит в шаровом слое пространства
- 38. Распределение молекул по абсолютным значениям скоростей т.к.
- 39. Джеймс Клерк Максвелл 1831-1879 Англия, Шотландия Разработал основы кинетической теории газов Основоположник теории электромагнитного поля Автор
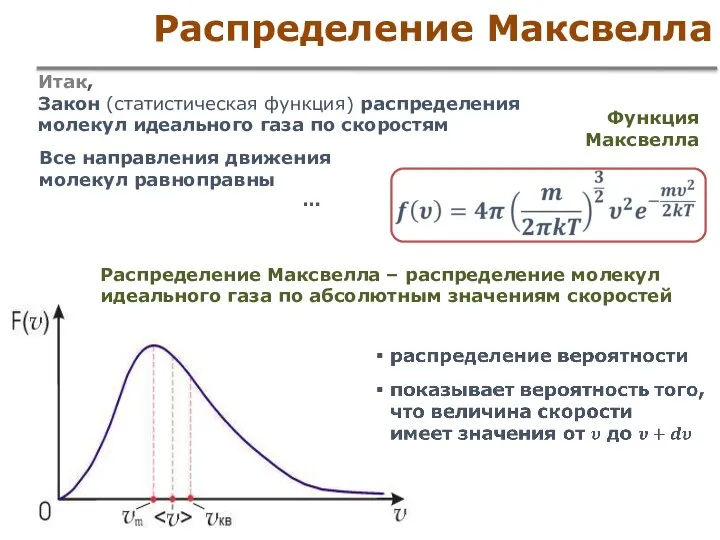
- 40. Распределение Максвелла Итак, Закон (статистическая функция) распределения молекул идеального газа по скоростям Распределение Максвелла – распределение
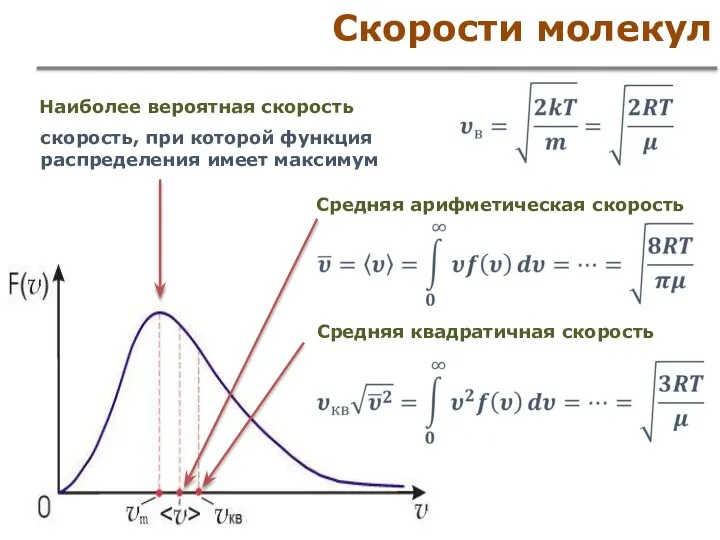
- 41. Скорости молекул Наиболее вероятная скорость скорость, при которой функция распределения имеет максимум Средняя арифметическая скорость Средняя
- 42. Средняя квадратичная скорость Средняя квадратичная скорость поступательного движения молекул идеального газа При 20°С Постоянная Больцмана Универсальная
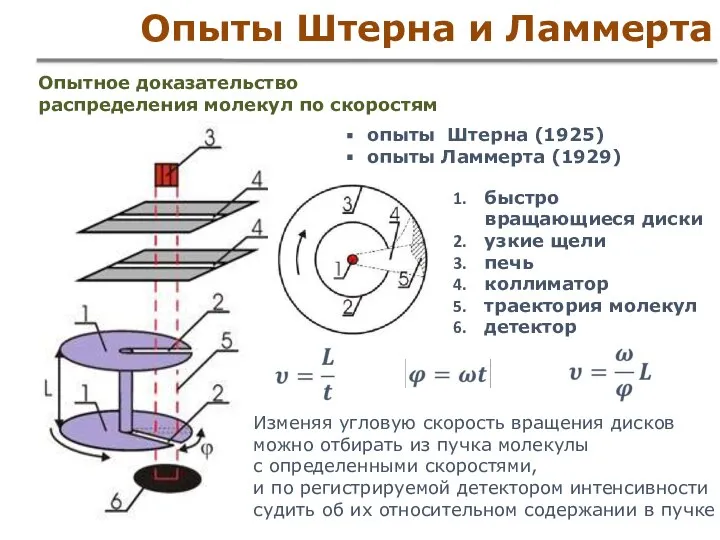
- 43. Опыты Штерна и Ламмерта Опытное доказательство распределения молекул по скоростям опыты Штерна (1925) опыты Ламмерта (1929)
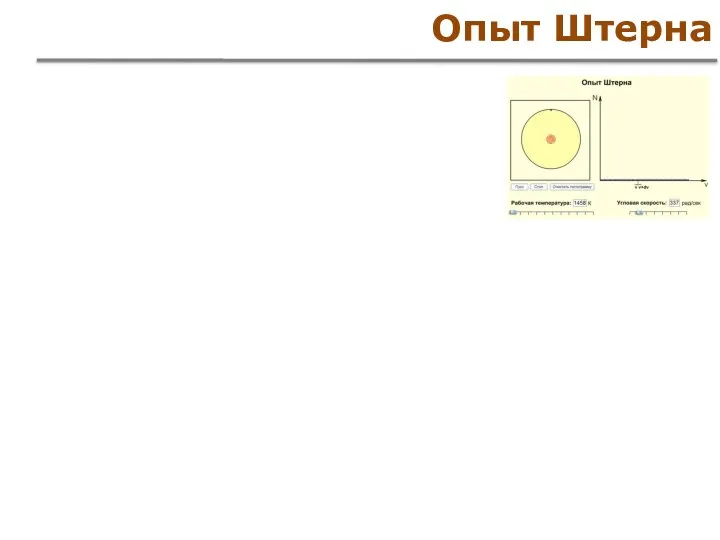
- 44. Опыт Штерна
- 45. Опыт Штерна
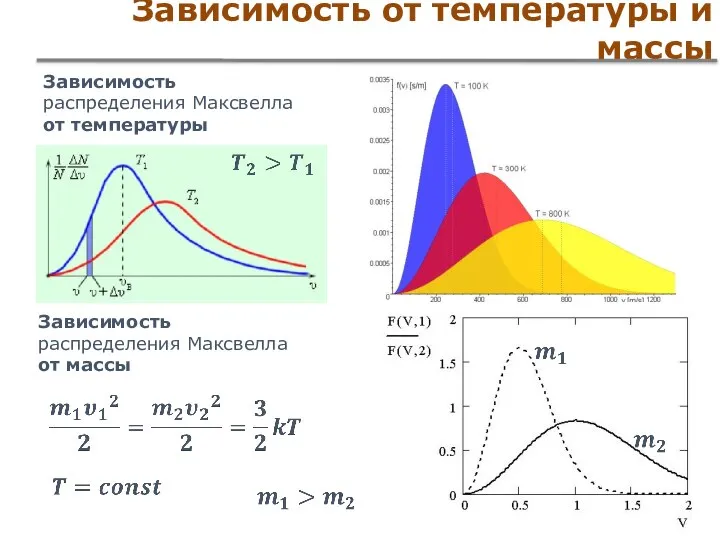
- 46. Зависимость от температуры и массы Зависимость распределения Максвелла от температуры Зависимость распределения Максвелла от массы
- 47. Барометрическая формула. Распределение Больцмана Молекулы атмосферного воздуха притягиваются к Земле Концентрация молекул убывает с увеличением высоты
- 48. Барометрическая формула Рассмотрим тонкий слой воздуха dh
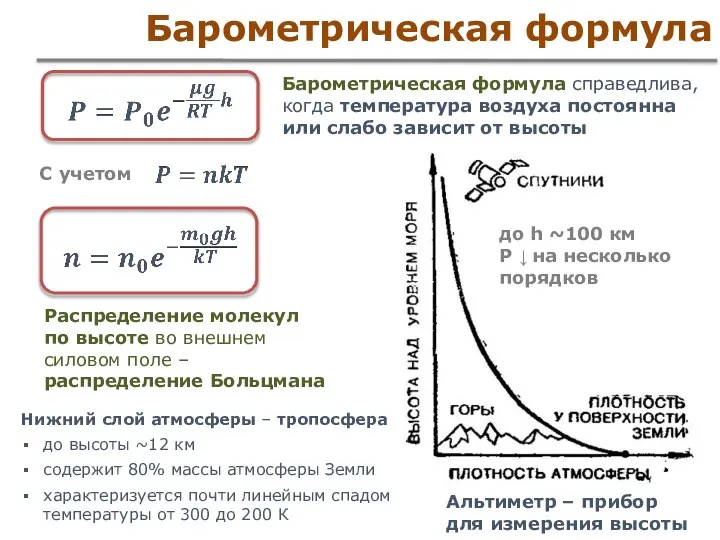
- 49. Барометрическая формула Барометрическая формула справедлива, когда температура воздуха постоянна или слабо зависит от высоты Нижний слой
- 50. Контрольные вопросы Термодинамическая температура газа изменилась на 10% На сколько процентов изменилась при этом средняя скорость
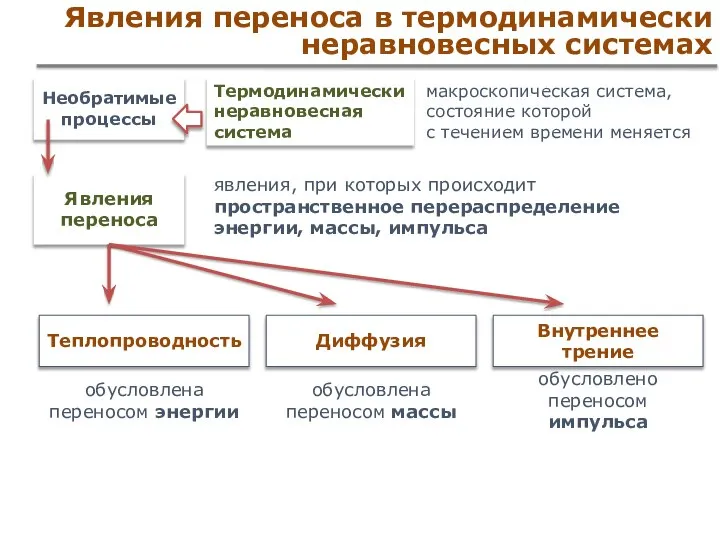
- 51. Явления переноса в термодинамически неравновесных системах Теплопроводность обусловлена переносом энергии Внутреннее трение обусловлено переносом импульса Диффузия
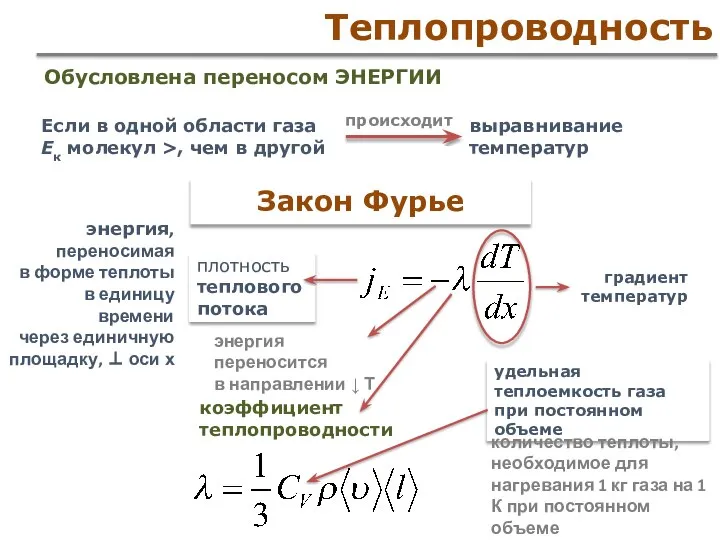
- 52. Теплопроводность Обусловлена переносом ЭНЕРГИИ Закон Фурье Если в одной области газа Ек молекул >, чем в
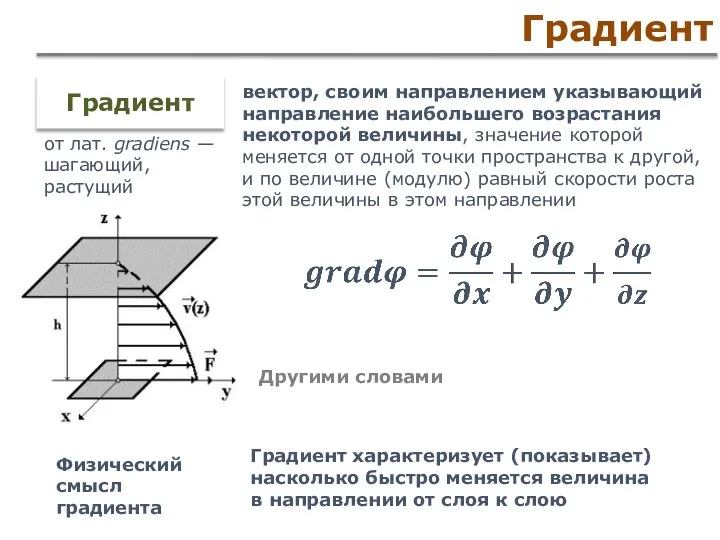
- 53. Градиент Градиент характеризует (показывает) насколько быстро меняется величина в направлении от слоя к слою Градиент от
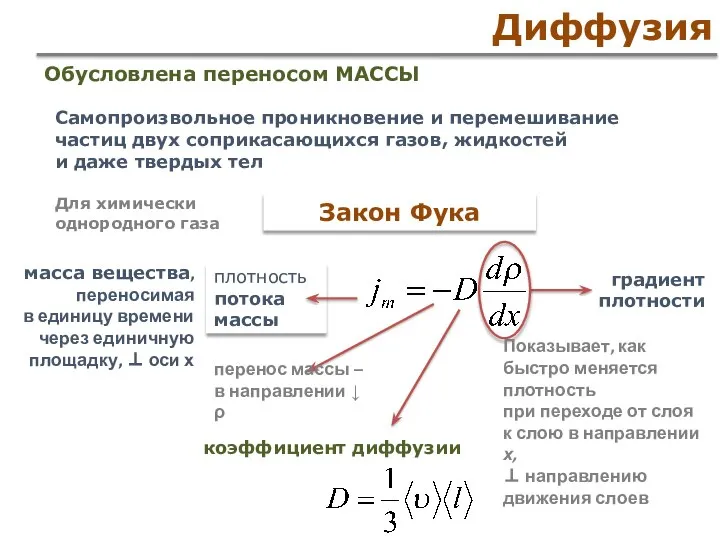
- 54. Диффузия Закон Фука Самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел
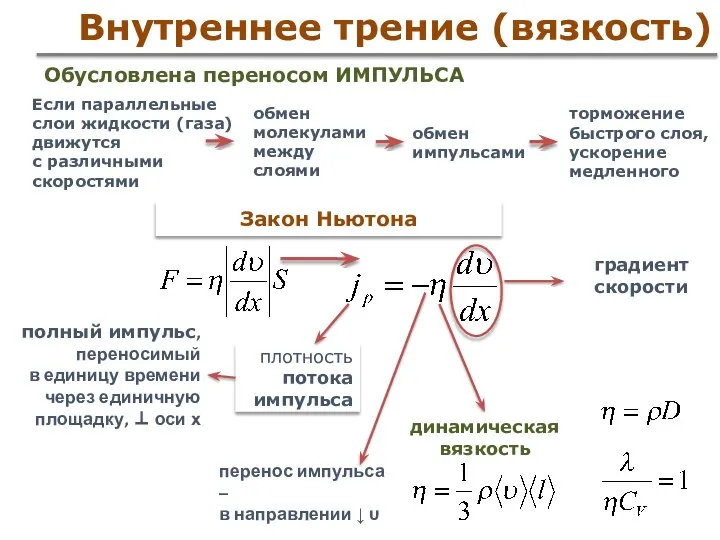
- 55. Внутреннее трение (вязкость) Закон Ньютона Если параллельные слои жидкости (газа) движутся с различными скоростями плотность потока
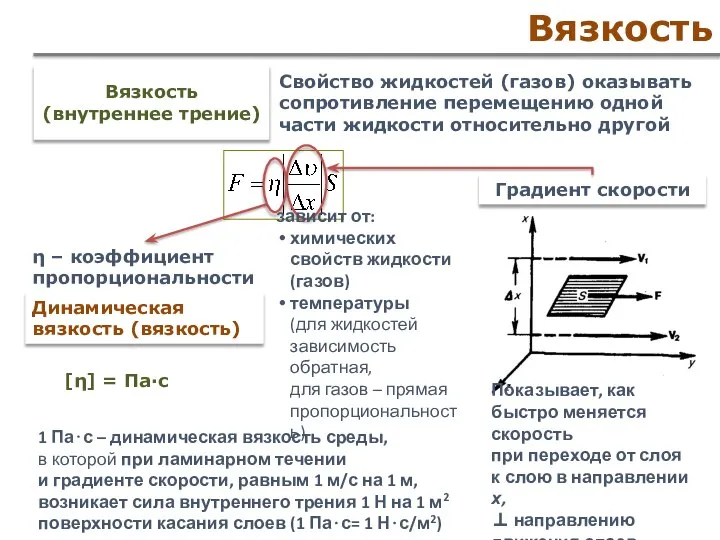
- 56. Вязкость Вязкость (внутреннее трение) Свойство жидкостей (газов) оказывать сопротивление перемещению одной части жидкости относительно другой Градиент
- 58. Скачать презентацию






























 Термодинамика
Термодинамика Модуль Юнга
Модуль Юнга Законы постоянного тока
Законы постоянного тока Расчет давления в жидкости
Расчет давления в жидкости Потери напряжения в элементах электрической цепи
Потери напряжения в элементах электрической цепи Динамика. Законы Ньютона
Динамика. Законы Ньютона Волновая оптика
Волновая оптика ГБОУ ЦО № 1631 Проектная работа «Чай из самовара» Выполнила: Антипова Я. Г., ученица 8 «А» класса Руководитель: Кор
ГБОУ ЦО № 1631 Проектная работа «Чай из самовара» Выполнила: Антипова Я. Г., ученица 8 «А» класса Руководитель: Кор Контрольная работа по теме МКТ
Контрольная работа по теме МКТ Циркуляция вод океана
Циркуляция вод океана Электрическая цепь. Электрическая схема. Условные обозначения
Электрическая цепь. Электрическая схема. Условные обозначения Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля I закон термодинамики
I закон термодинамики Исследование агрегатов и систем автомобилей
Исследование агрегатов и систем автомобилей Законы природы, проявления законов
Законы природы, проявления законов Винайдення фотографий
Винайдення фотографий Презентация на тему Этапы развития средств связи
Презентация на тему Этапы развития средств связи  151c81f567f6a33917e4696ac6d03f7b
151c81f567f6a33917e4696ac6d03f7b Паровые двигатели
Паровые двигатели Закон Ома для участка цепи
Закон Ома для участка цепи Полная работа системы
Полная работа системы Механическая работа
Механическая работа Вращение шестеренки
Вращение шестеренки Удивительное электричество
Удивительное электричество Презентация на тему Электрическая цепь
Презентация на тему Электрическая цепь  Катушки индуктивности
Катушки индуктивности Открытие явления электромагнитной индукции
Открытие явления электромагнитной индукции Газовые законы
Газовые законы