Движение тела, брошенного вертикально

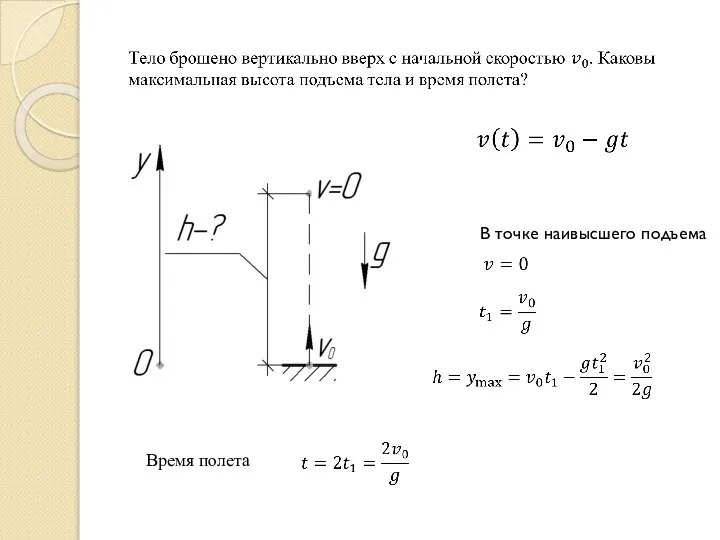
В точке наивысшего подъема
Время полета

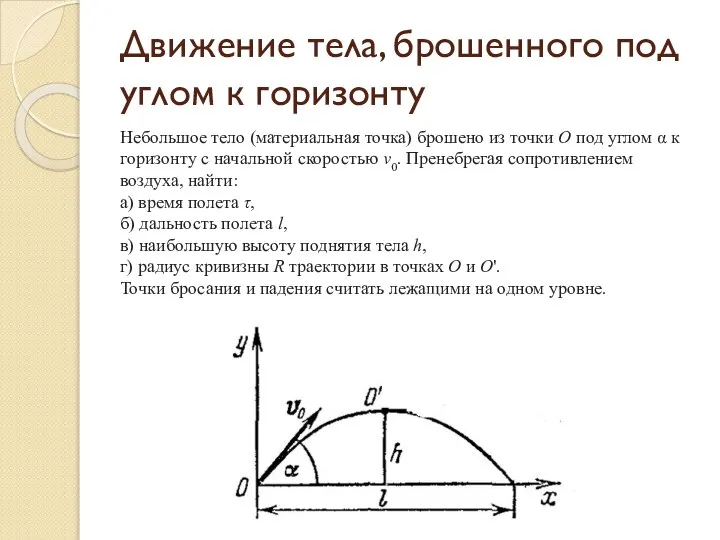
Движение тела, брошенного под углом к горизонту
Небольшое тело (материальная точка) брошено из точки О под углом α к горизонту с начальной скоростью v0. Пренебрегая сопротивлением воздуха, найти:
а) время полета τ,
б) дальность полета l,
в) наибольшую высоту поднятия тела h,
г) радиус кривизны R траектории в точках О и О'.
Точки бросания и падения считать лежащими на одном уровне.

Тело движется с постоянным ускорением:

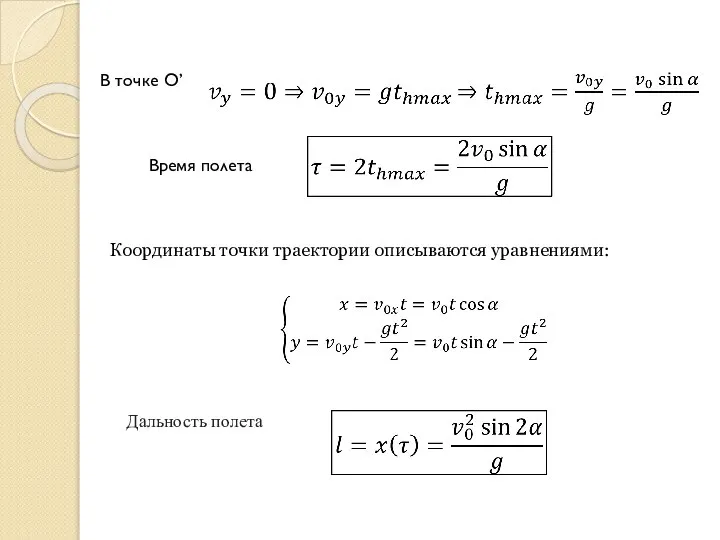
В точке О’
Координаты точки траектории описываются уравнениями:
Время полета
Дальность полета

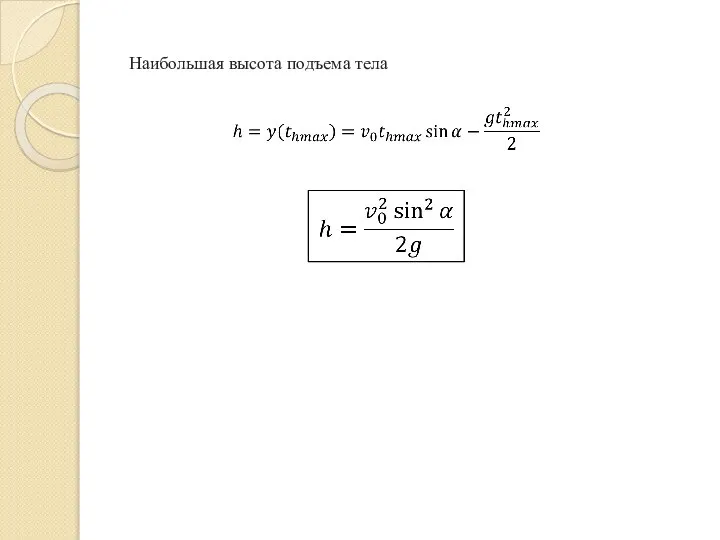
Наибольшая высота подъема тела

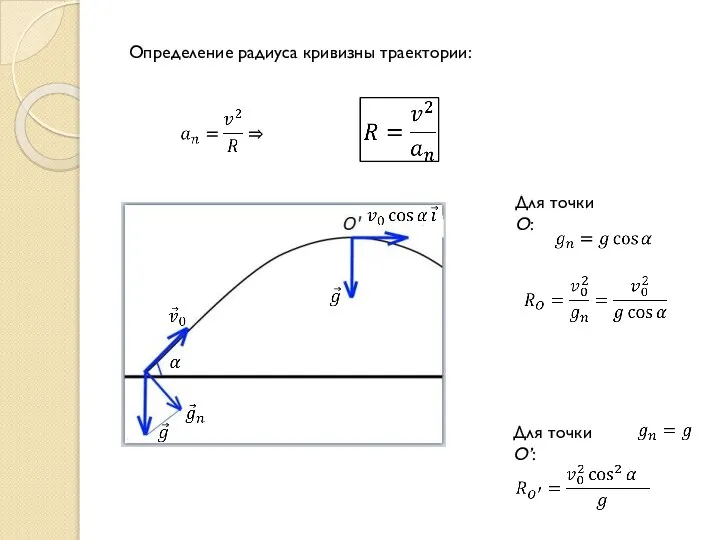
Определение радиуса кривизны траектории:
Для точки О:
Для точки О’:

Равномерное вращение
число оборотов в единицу времени или ЧАСТОТА ВРАЩЕНИЯ

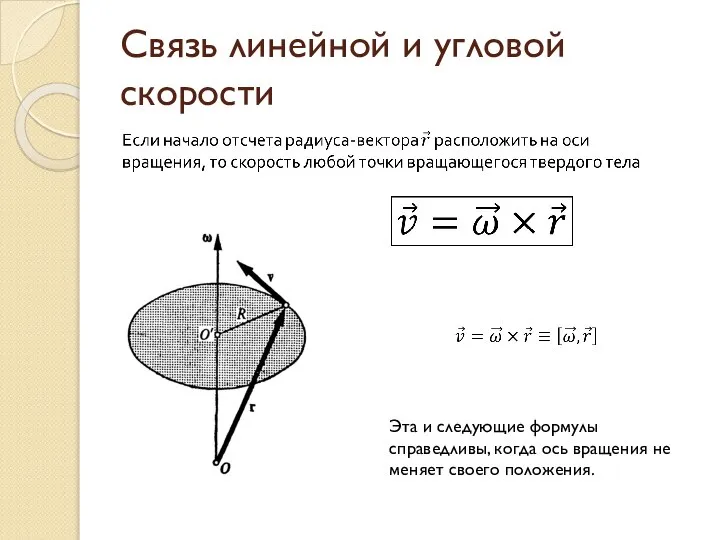
Связь линейной и угловой скорости
.

Связь линейной и угловой скорости
Эта и следующие формулы справедливы, когда ось вращения не меняет своего положения.

Связь углового и линейного ускорения

Угловое и линейное ускорение
Если расстояние точки твердого тела до оси вращения равно R, то

Аналогии поступательного и вращательного движений

Формулы кинематики

Динамика
(от греч. dynamis - сила) - раздел механики, посвящённый изучению движения материальных тел под действием приложенных к ним сил.

Классическая динамика
Движения любых материальных тел (кроме микрочастиц), происходящие со скоростями, не близкими к скорости света.

Динамика поступательного движения
Исаак Ньютон
(1642-1727)
Ньютон в 1687 г. опубликовал книгу «Математические основы натуральной философии».

Первый закон Ньютона
Закон инерции – это первый закон Ньютона: если тело предоставлено самому себе, то есть результирующая действующих на него сил равна нулю, то оно остается в состоянии покоя или равномерного прямолинейного движения.

Из первого закона Ньютона следует важный физический принцип: существование так называемой инерциальной системы отсчета.
ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЁТА - система отсчёта, в к-рой справедлив закон инерции: материальная точка, когда на неё не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.
Инерциальная система отсчёта

Инертность
ИНЕРТНОСТЬ (инерция) (от лат. iners, род. падеж inertis - бездеятельный) в механике - свойство материальных тел, проявляющееся в том, что тело сохраняет неизменным состояние своего движения или покоя по отношению к инерциальной системе отсчёта, когда внеш. воздействия на тело (силы) отсутствуют или взаимно уравновешиваются.
Масса – мера инертности тела (при поступательном движении).

Второй закон Ньютона

Основное уравнение движения
(основное уравнение динамики поступательного движения)
Второй закон Ньютона – это
основное уравнение движения.

Третий закон Ньютона

Прямая задача динамики