Содержание
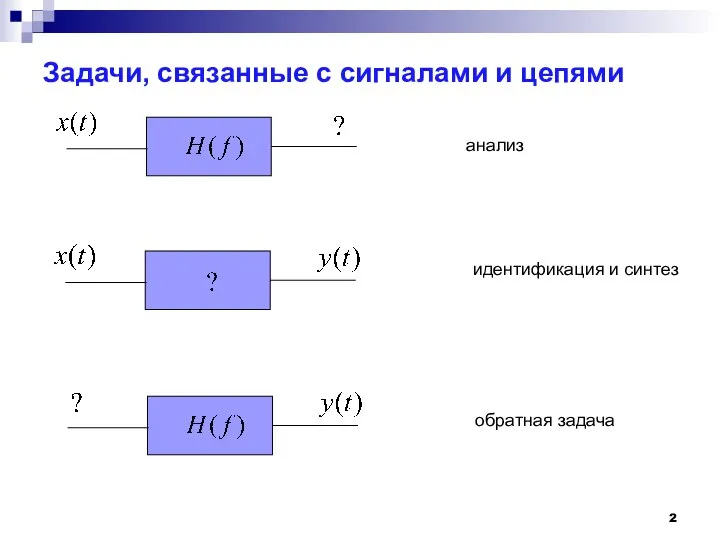
- 2. Задачи, связанные с сигналами и цепями анализ идентификация и синтез обратная задача
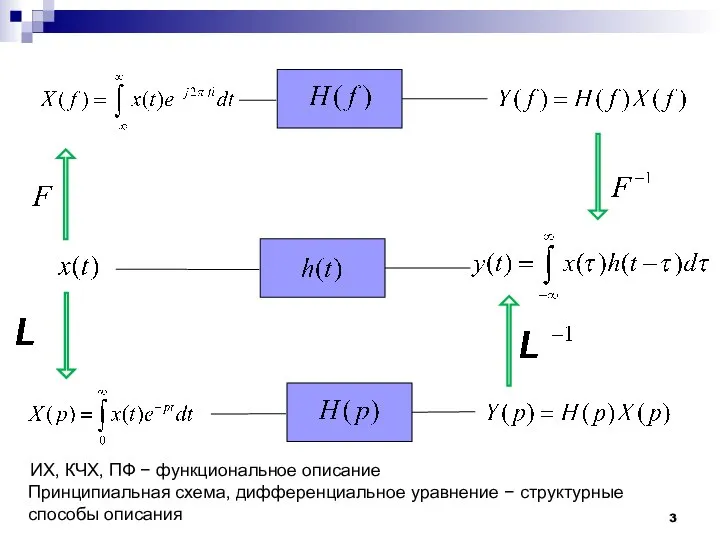
- 3. ИХ, КЧХ, ПФ − функциональное описание Принципиальная схема, дифференциальное уравнение − структурные способы описания
- 4. Точные методы анализа ЛИС-цепей: Временной метод (интеграл Дюамеля) Метод, основанный на решении дифференциального уравнения цепи Операторный
- 5. (ЛИС-цепи с распределенными параметрами описываются линейными дифференциальными уравнениями в частных производных с постоянными коэффициентами) Метод, основанный
- 6. Линейные ДУ с постоянными коэффициентами Если входной сигнал задан, то тем самым задана вся правая часть
- 7. Решение ЛДУ с ПК (пример см. в учебнике) Если все корни простые, то общее решение однородного
- 8. Связь спектрального метода с ДУ Пусть на вход ЛИС-цепи воздействует Тогда
- 9. Итак, КЧХ любой ЛИС-цепи имеет вид функции, дробно-рациональной относительно Пример неоднородное ДУ однородное ДУ
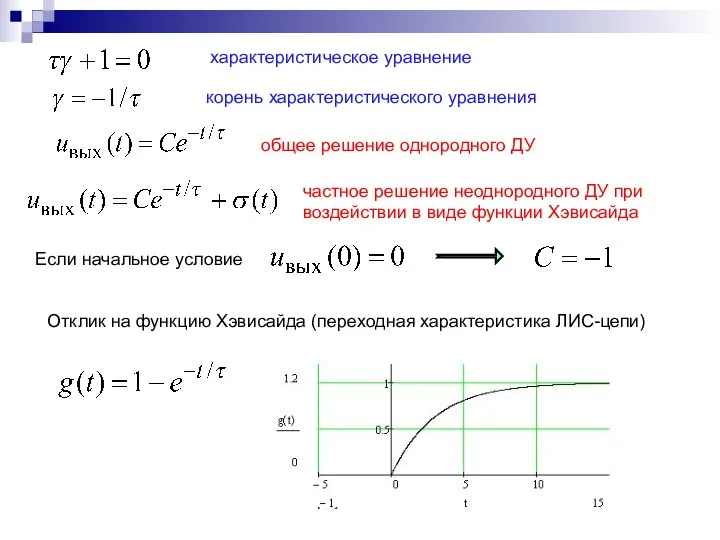
- 10. характеристическое уравнение корень характеристического уравнения общее решение однородного ДУ частное решение неоднородного ДУ при воздействии в
- 11. Если на входе дельта-функция (сп. плотность ≡1) Обратным преобразованием Фурье получаем отклик − ИХ
- 12. Операторный метод Дифференциальное уравнение заменяется алгебраическим операторная передаточная функция
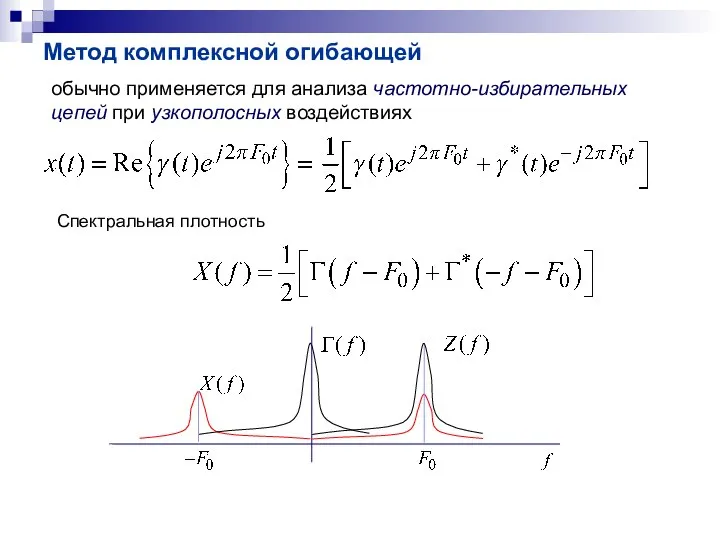
- 13. Метод комплексной огибающей обычно применяется для анализа частотно-избирательных цепей при узкополосных воздействиях Спектральная плотность
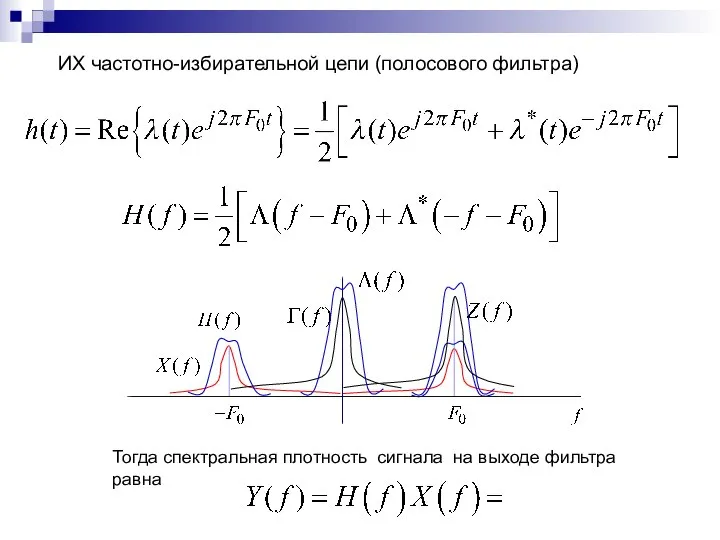
- 14. ИХ частотно-избирательной цепи (полосового фильтра) Тогда спектральная плотность сигнала на выходе фильтра равна
- 15. где Низкочастотный эквивалент ЧИЦ имеет ИХ Итак,
- 16. НЕСТАЦИОНАРНЫЕ ЛИНЕЙНЫЕ ЦЕПИ
- 17. Линейные нестационарные цепи Линейные нестационарные цепи с сосредоточенными параметрами описываются обыкновенными линейными дифференциальными уравнениями с переменными
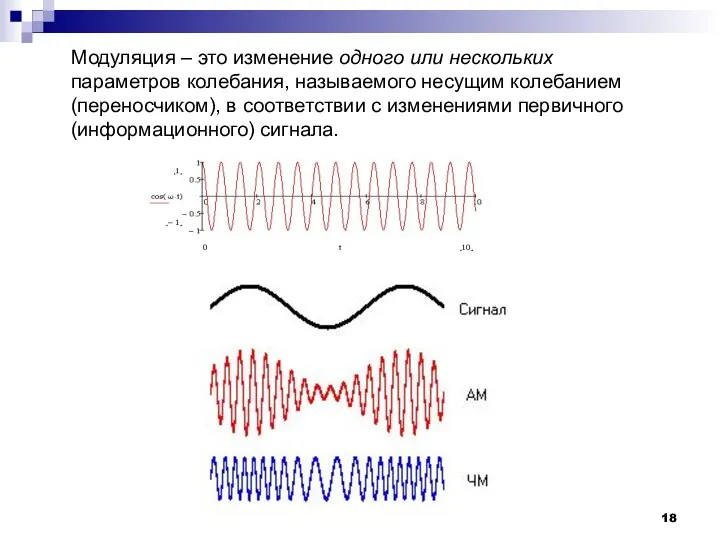
- 18. Модуляция – это изменение одного или нескольких параметров колебания, называемого несущим колебанием (переносчиком), в соответствии с
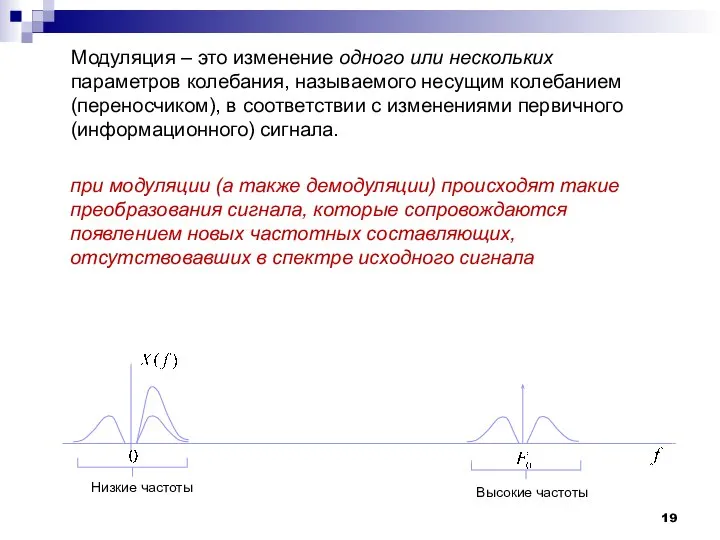
- 19. Модуляция – это изменение одного или нескольких параметров колебания, называемого несущим колебанием (переносчиком), в соответствии с
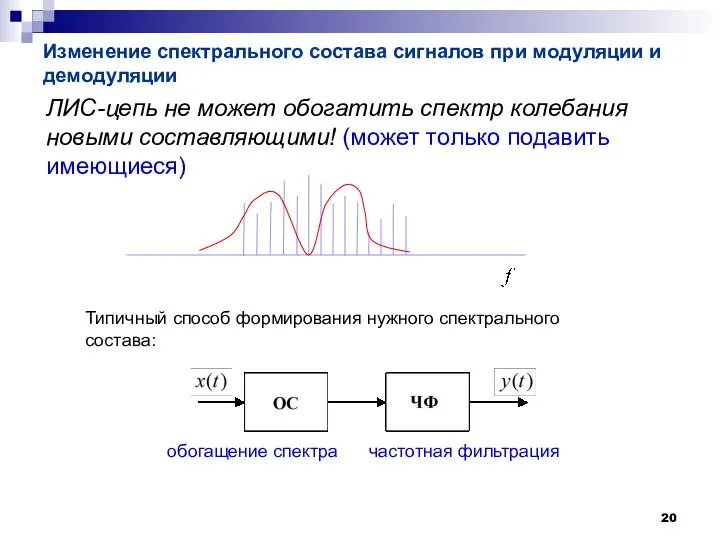
- 20. Изменение спектрального состава сигналов при модуляции и демодуляции ЛИС-цепь не может обогатить спектр колебания новыми составляющими!
- 21. Линейные нестационарные цепи где h(t,τ) - отклик цепи в момент t на входной сигнал в виде
- 22. Линейные нестационарные цепи Пусть на входе колебание Однако эта функция зависит не только от частоты, но
- 23. подставим обратное ПФ для входного сигнала Это не спектральная плотность !!!
- 24. Воздействие гармонического колебания на линейную параметрическую цепь проводимость (крутизна ВАХ) Простейший случай − напряжение и крутизна
- 26. Скачать презентацию















 Движение твердой среды
Движение твердой среды Визначення температури спалаху та самозапалення нафтопродуктів. Практичне заняття № 6
Визначення температури спалаху та самозапалення нафтопродуктів. Практичне заняття № 6 Игра К вершинам физики
Игра К вершинам физики Презентация на тему Электромагнитные колебания
Презентация на тему Электромагнитные колебания  Современная физическая картина мира
Современная физическая картина мира Демонстрационный вариант контрольных измерительных материалов для проведения в 2016 году государственного экзамена по физике
Демонстрационный вариант контрольных измерительных материалов для проведения в 2016 году государственного экзамена по физике Элементы теории упругости, тензоры деформаций и напряжений
Элементы теории упругости, тензоры деформаций и напряжений Система электрического пуска
Система электрического пуска Презентация на тему Простые механизмы. Рычаг
Презентация на тему Простые механизмы. Рычаг  Теорія лінійних систем автоматичного керування. Лекція 2
Теорія лінійних систем автоматичного керування. Лекція 2 Дисперсия света. Опыт И. Ньютона
Дисперсия света. Опыт И. Ньютона Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Электростатика 11
Электростатика 11 Модель бульдозера
Модель бульдозера Физические величины и единицы измерения. Лабораторная работа 1
Физические величины и единицы измерения. Лабораторная работа 1 Презентация на тему Модели атома
Презентация на тему Модели атома  Ядерное оружие
Ядерное оружие Аварийная остойчивость. Спрямление судна
Аварийная остойчивость. Спрямление судна Ультрафиолетовое излучение
Ультрафиолетовое излучение Сообщающиеся сосуды
Сообщающиеся сосуды Движение жидкостей и газов. Закон Бернулли
Движение жидкостей и газов. Закон Бернулли Законы проведения возбуждения по нервному волокну. Парабиоз. Физиологические свойства синапсов
Законы проведения возбуждения по нервному волокну. Парабиоз. Физиологические свойства синапсов Магнитные подшипники
Магнитные подшипники Своя игра. 7 класс
Своя игра. 7 класс Александр Степанович Попов - изобретатель радио
Александр Степанович Попов - изобретатель радио Научно-исследовательская работа. Парадоксы физики
Научно-исследовательская работа. Парадоксы физики Интерференция и дифракция света
Интерференция и дифракция света Самостоятельная работа 66 урок
Самостоятельная работа 66 урок