Диффузия в экспериментах ЯМР

Уравнения Блоха-Торри (диффузия)
Изотропная диффузия
Анизотропная диффузия
Квантовая радиофизика
Диффузия в экспериментах ЯМР

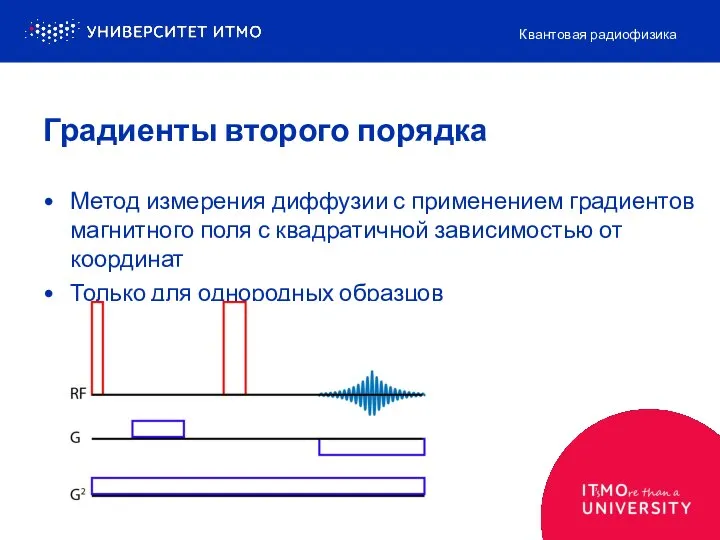
Метод измерения диффузии с применением градиентов магнитного поля с квадратичной зависимостью от координат
Только для однородных образцов
Квантовая радиофизика
Градиенты второго порядка

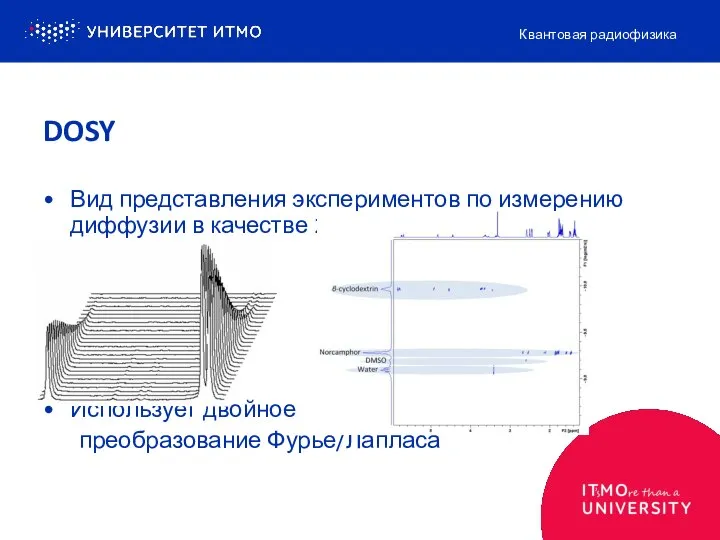
Вид представления экспериментов по измерению диффузии в качестве 2D-графиков
Использует двойное
преобразование Фурье/Лапласа
Квантовая радиофизика
DOSY

Экспериментальные помехи при измерении движения

Radiation damping
Неоднородность поля
Температурная нестабильность
Фоновые градиенты
Квантовая радиофизика
Экспериментальные помехи

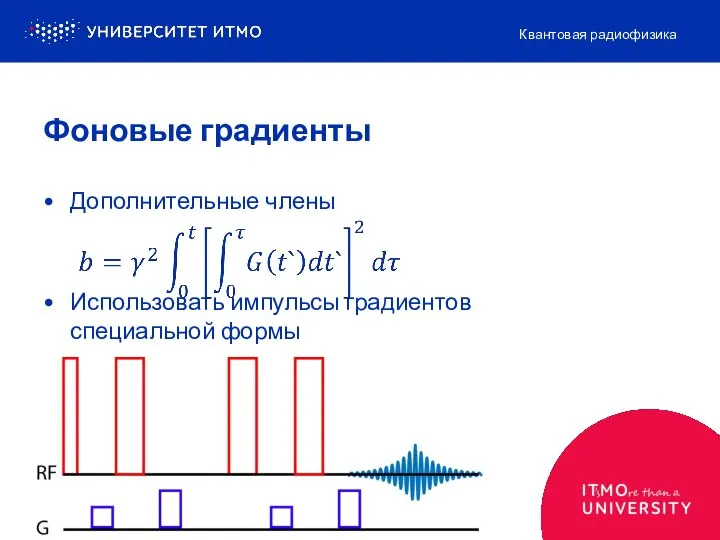
Дополнительные члены
Использовать импульсы градиентов специальной формы
Квантовая радиофизика
Фоновые градиенты

Вихревые токи в экспериментах с градиентами магнитного поля
Неравномерность накопления фазы
Изменение формы импульса градиента
Квантовая радиофизика
Вихревые токи

Диффузия в замкнутых пространствах

Наличие физических ограничений для движения частиц приводит к ограничению подвижности
Квантовая радиофизика
Ограниченная диффузия в ЯМР

Введение q-пространства для оценки подвижности частиц
Вводится через рассмотрение уравнений диффузии для вероятности перемещения частицы
Фазовый сдвиг переместившейся частицы
Квантовая радиофизика
Фазовое q-пространство

P(x0,x1,Δ) – вероятность частицы, находящейся в точке x0 сместиться за время Δ в точку x1
При использовании понятия пропагатора изменение сигнала ЯМР вследствие диффузии можно записать
Описывает движение в системе
Квантовая радиофизика
Пропагатор частицы

Так как в выражении для E есть усреднение по начальному положению, то можно рассматривать усредненный пропагатор – функцию смещения частицы
Кроме того можно рассматривать только однородные объекты, то есть с постоянным ρ(x0)
Таким образом, изменение сигнала ЯМР является Фурье-образом усреденного пропагатора
Квантовая радиофизика
Пропагатор смещения частицы

При малых временах измерения Δ можно измерить пропагатор и связать его с среднеквадратичным смещением частицы (или с коэффициентом самодиффузии)
В случае свободной гауссовой диффузии полуширина функции пропагатора
Квантовая радиофизика
Измерение пропагатора