Содержание
- 2. ДИНАМИКА. Законы Ньютона Динамика изучает движение тел в связи с теми причинами (взаимодействиями между телами), которые
- 3. ДИНАМИКА. Законы Ньютона Первый закон Ньютона. Тело сохраняет состояние покоя или равномерного и прямолинейного движения до
- 4. ДИНАМИКА. Законы Ньютона Общая физика. Раздел «Основы классической механики» Кафедра физики Красивые ролики с движением Солнечной
- 5. ДИНАМИКА. Принцип относительности Галилея Совокупность этих четырех уравнений называется преобразованиями Галилея Рассмотрим две системы отсчета, движущиеся
- 6. Продифференцировав полученные соотношения получим: Важным свойством инерциальных систем является их инвариантность по отношению к преобразованию координат
- 7. Общая физика. Раздел «Основы классической механики» Положение о том, что все механические явления в различных инерциальных
- 8. Общая физика. Раздел «Основы классической механики» Кафедра физики ДИНАМИКА. Принцип относительности Галилея Уединитесь в просторное помещение
- 9. ДИНАМИКА. Законы Ньютона Общая физика. Раздел «Основы классической механики» СИЛА, МАССА Сила – это общая мера
- 10. ДИНАМИКА. Законы Ньютона Общая физика. Раздел «Основы классической механики» ИМПУЛЬС ТЕЛА , или Полный импульс замкнутой
- 11. ДИНАМИКА. Законы Ньютона Общая физика. Раздел «Основы классической механики» Если известна зависимость силы от координат и
- 12. ДИНАМИКА. Законы Ньютона Общая физика. Раздел «Основы классической механики» Кафедра физики Третий закон Ньютона называют законом
- 13. ДИНАМИКА. Законы Ньютона, применимость Общая физика. Раздел «Основы классической механики» Кафедра физики ВОПРОС: Мысленный эксперимент –
- 14. ДИНАМИКА. Законы сохранения в механике Общая физика. Раздел «Основы классической механики» Силы, действующие на тела системы:
- 15. В соответствии с третьим законом Ньютона . ДИНАМИКА. Закон сохранения импульса Общая физика. Раздел «Основы классической
- 16. ДИНАМИКА. Закон сохранения импульса Общая физика. Раздел «Основы классической механики» - обобщение второго закона Ньютона для
- 17. ДИНАМИКА. Центр инерции Общая физика. Раздел «Основы классической механики» Вернемся к второму закону Ньютона для механической
- 18. ДИНАМИКА. Центр инерции Общая физика. Раздел «Основы классической механики» В итоге получим соотношение: Центр инерции системы
- 19. ДИНАМИКА. Центр инерции Общая физика. Раздел «Основы классической механики» Скорость движения центра инерции: Движение центра инерции
- 20. ДИНАМИКА. Силы. Общая физика. Раздел «Основы классической механики» В современной физике различают четыре вида взаимодействий: Кафедра
- 21. ДИНАМИКА. Закон всемирного тяготения. Общая физика. Раздел «Основы классической механики» В Аристотелевой картине мира не было
- 22. ДИНАМИКА. Закон всемирного тяготения. Общая физика. Раздел «Основы классической механики» На основании точнейших наблюдений того времени,
- 23. ДИНАМИКА. Закон всемирного тяготения. Общая физика. Раздел «Основы классической механики» Кафедра физики где G - фундаментальная
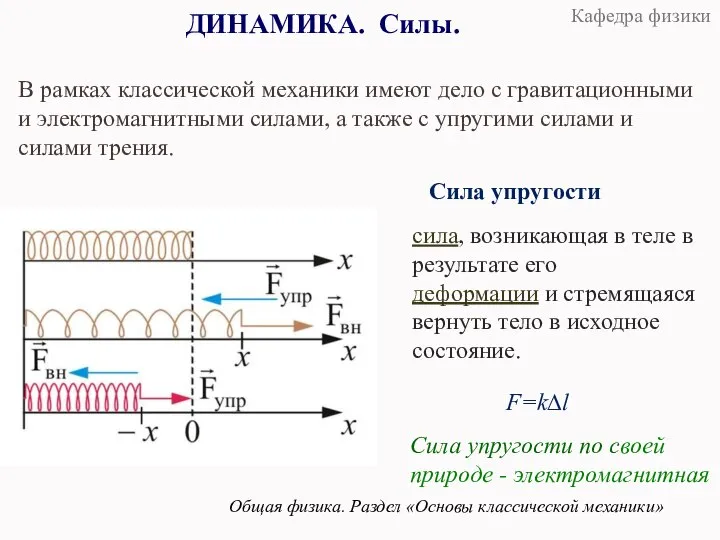
- 24. ДИНАМИКА. Силы. Общая физика. Раздел «Основы классической механики» В рамках классической механики имеют дело с гравитационными
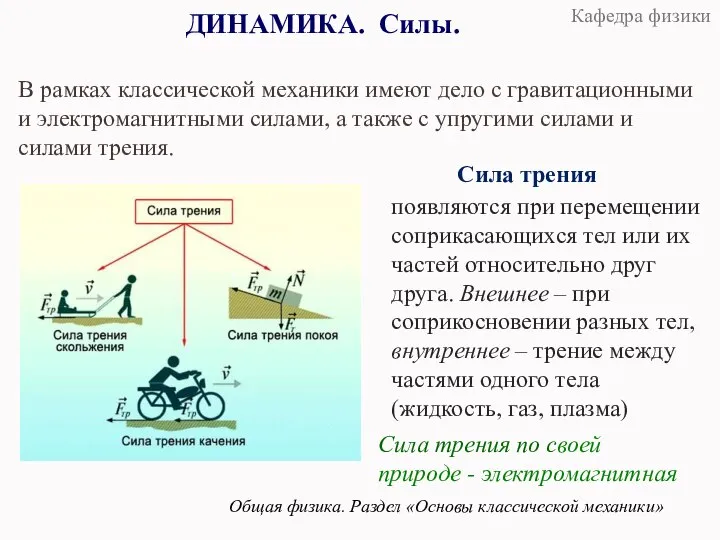
- 25. ДИНАМИКА. Силы. Общая физика. Раздел «Основы классической механики» В рамках классической механики имеют дело с гравитационными
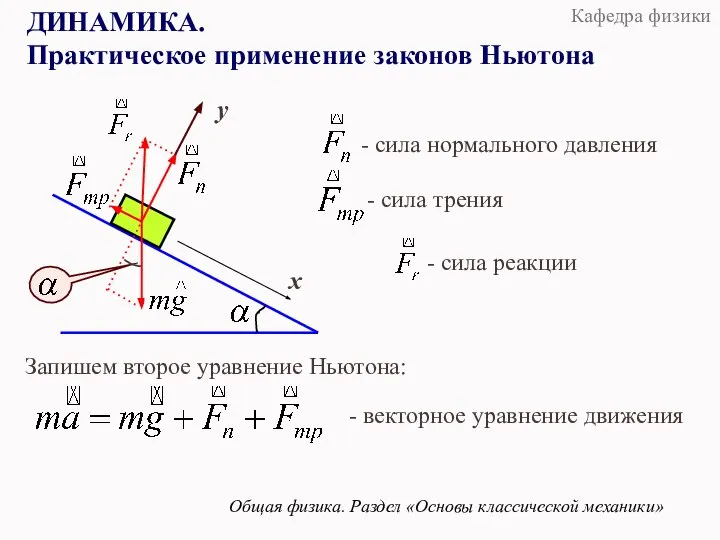
- 26. ДИНАМИКА. Практическое применение законов Ньютона Общая физика. Раздел «Основы классической механики» x - сила нормального давления
- 27. ДИНАМИКА. Практическое применение законов Ньютона Общая физика. Раздел «Основы классической механики» Запишем уравнения движения в проекциях
- 29. Скачать презентацию























 Движение в неинерциальных системах отсчёта
Движение в неинерциальных системах отсчёта Волновые свойства частиц
Волновые свойства частиц Виды машин, применяемые в швейной промышленности
Виды машин, применяемые в швейной промышленности Кинематика точки. Основные определения и понятия
Кинематика точки. Основные определения и понятия Современные способы и методы контроля и регулировки судовых дизельных двигателей
Современные способы и методы контроля и регулировки судовых дизельных двигателей Динамика. Первый закон Ньютона
Динамика. Первый закон Ньютона Графическое представление результатов измерений
Графическое представление результатов измерений Программа элективного курса: Чудеса физики
Программа элективного курса: Чудеса физики Паровая турбина. КПД
Паровая турбина. КПД Двигатель Стирлинга
Двигатель Стирлинга Построение изображеия в линзах и формула линзы. 11 класс
Построение изображеия в линзах и формула линзы. 11 класс Электростатика. Электродинамика
Электростатика. Электродинамика Электрический ток в полупроводниках работа по физике ученицы 10 «В» Заусской Анастасии
Электрический ток в полупроводниках работа по физике ученицы 10 «В» Заусской Анастасии Волосяной гигрометр
Волосяной гигрометр Моделирование аксиально-поршневой гидромашины с раздельными цилиндрами
Моделирование аксиально-поршневой гидромашины с раздельными цилиндрами Цвет. Основы цветоведения
Цвет. Основы цветоведения Устройство сверлильного станка
Устройство сверлильного станка Волны и оптика. Лекция 03
Волны и оптика. Лекция 03 Зависимость силы тока от напряжения
Зависимость силы тока от напряжения Автоматизированная информационная система Техосмотр
Автоматизированная информационная система Техосмотр Электрический ток в газах
Электрический ток в газах Дифракция света. Тема 2
Дифракция света. Тема 2 Рычаг. Самостоятельная работа
Рычаг. Самостоятельная работа Физика космоса, кружок. Космология в ОТО
Физика космоса, кружок. Космология в ОТО Презентация на тему Двигатель внутреннего сгорания: принципы
Презентация на тему Двигатель внутреннего сгорания: принципы  Законы постоянного тока. Энергия конденсаторов.
Законы постоянного тока. Энергия конденсаторов. Электростатика. Контрольная работа
Электростатика. Контрольная работа Общие теоремы динамики
Общие теоремы динамики