Динамика. Лекция 8

Лекция 8
Законы сохранения. Элементы теории моментов инерции. Кинетический момент твердого тела. Дифференциальное уравнение вращения твердого тела. Пример решения задачи на использование теоремы об изменении момента количества движения системы. Элементарная теория гироскопа.

1
2. Момент инерции твердого тела относительно оси:
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси.
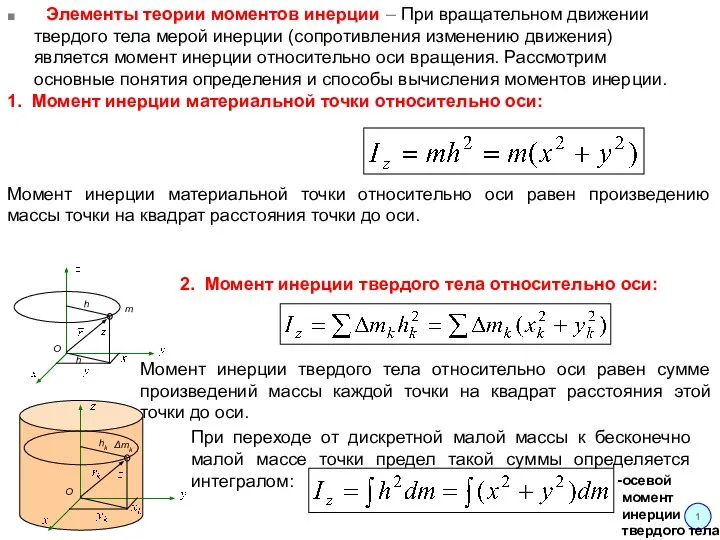
Момент инерции твердого тела относительно оси равен сумме произведений массы каждой точки на квадрат расстояния этой точки до оси.
■ Элементы теории моментов инерции – При вращательном движении твердого тела мерой инерции (сопротивления изменению движения) является момент инерции относительно оси вращения. Рассмотрим основные понятия определения и способы вычисления моментов инерции.
1. Момент инерции материальной точки относительно оси:
При переходе от дискретной малой массы к бесконечно малой массе точки предел такой суммы определяется интегралом:
осевой момент
инерции
твердого тела.

2
Кроме осевого момента инерции твердого тела существуют другие виды моментов инерции: центробежный момент инерции твердого тела.
полярный момент инерции твердого тела.
3. Теорема о моментах инерции твердого тела относительно параллельных осей – формула перехода к параллельным осям:
Таким образом:
Если ось z1 проходит через центр масс, то статические моменты равны нулю:

3
Момент инерции однородного стержня постоянного сечения относительно оси:
x
z
L
Выделим элементарный объем dV = Adx
на расстоянии x:
x
dx
Элементарная масса:
Для вычисления момента инерции относительно центральной оси (проходящей через центр тяжести) достаточно изменить расположение оси и задать пределы интегрирования (-L/2, L/2). Здесь продемонстрируем формулу перехода к параллельным
осям:
zС
5. Момент инерции однородного сплошного цилиндра относительно оси симметрии:
H
dr
r
Выделим элементарный объем dV = 2πrdrH
(тонкий цилиндр радиуса r) :
Элементарная масса:
Здесь использована формула объема цилиндра V=πR2H.
Для вычисления момента инерции пустотелого (толстого) цилиндра достаточно задать пределы интегрирования от R1 до R2 (R2> R1):
C
Поскольку высота цилиндров в результате не входит в формулы моментов инерции, то они остаются справедливыми для тонкого сплошного диска и обода колеса (тонкого кольца).

4
6. Момент инерции тонкого цилиндра относительно оси симметрии ( t <
H
В силу малости толщины цилиндра
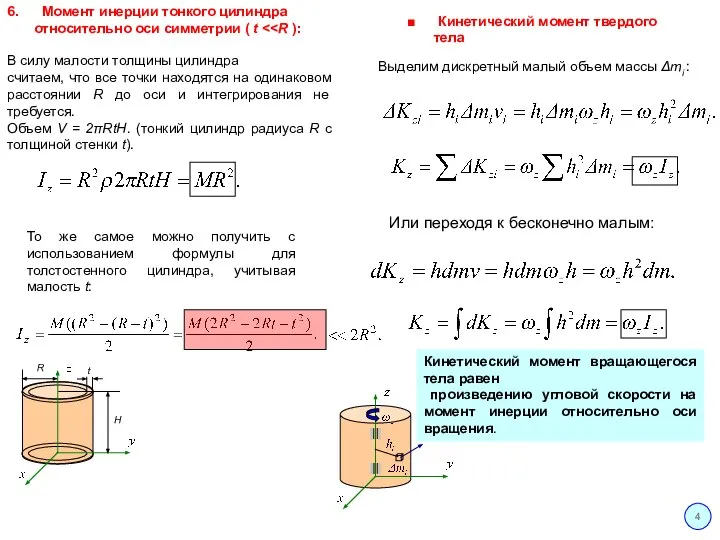
считаем, что все точки находятся на одинаковом расстоянии R до оси и интегрирования не требуется.
Объем V = 2πRtH. (тонкий цилиндр радиуса R с толщиной стенки t).
То же самое можно получить с использованием формулы для толстостенного цилиндра, учитывая малость t:
■ Кинетический момент твердого тела
Выделим дискретный малый объем массы Δmi :
Или переходя к бесконечно малым:
Кинетический момент вращающегося тела равен
произведению угловой скорости на момент инерции относительно оси вращения.

5
Пример: Два человека одинакового веса G1 = G2 висят на канате, переброшенном через сплошной блок весом G3 = G1/4. В некоторый момент один из них начал подниматься по канату с относительной скоростью u. Определить скорости подъема каждого из людей.
1. Выбираем объект движения (блок с людьми):
2. Отбрасываем связи (опорное устройство блока):
3. Заменяем связь реакциями (подшипника):
4. Добавляем активные силы (силы тяжести):
5. Записываем теорему об изменении кинетического момента системы относительно оси вращения блока:
R
Так как момент внешних сил равен нулю, то кинетический момент должен оставаться постоянным:
В начальный момент времени t = 0 было равновесие и Kz0 = 0.
После начала движения одного человека относительно каната вся система пришла в движение, но кинетический момент системы должен остаться равным нулю: Kz = 0.
Кинетический момент системы складывается из кинетических моментов обоих людей и блока:
Здесь v2 – скорость второго человека, равная скорости троса,