Содержание
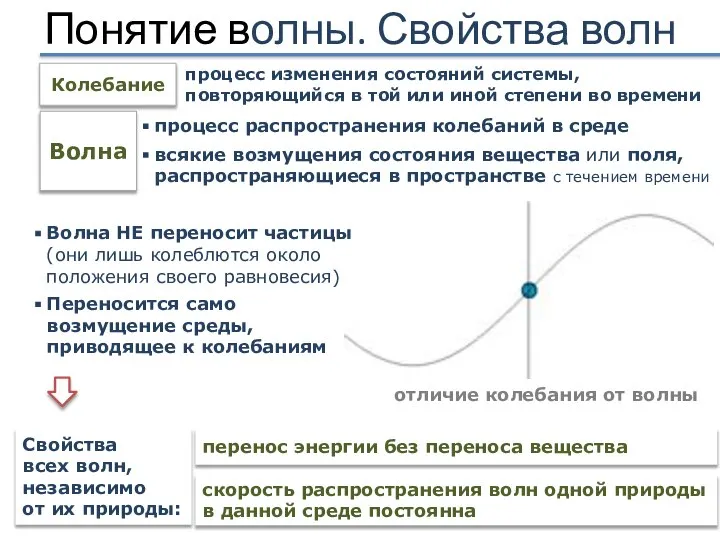
- 2. Понятие волны. Свойства волн Волна процесс распространения колебаний в среде всякие возмущения состояния вещества или поля,
- 3. Классификация волн По физической природе и типу колеблющейся величины звук свет
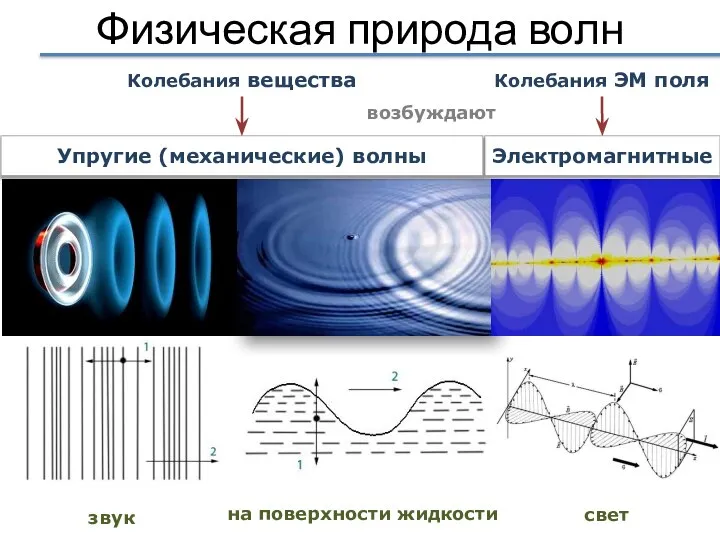
- 4. Физическая природа волн на поверхности жидкости Электромагнитные Упругие (механические) волны Колебания ЭМ поля Колебания вещества свет
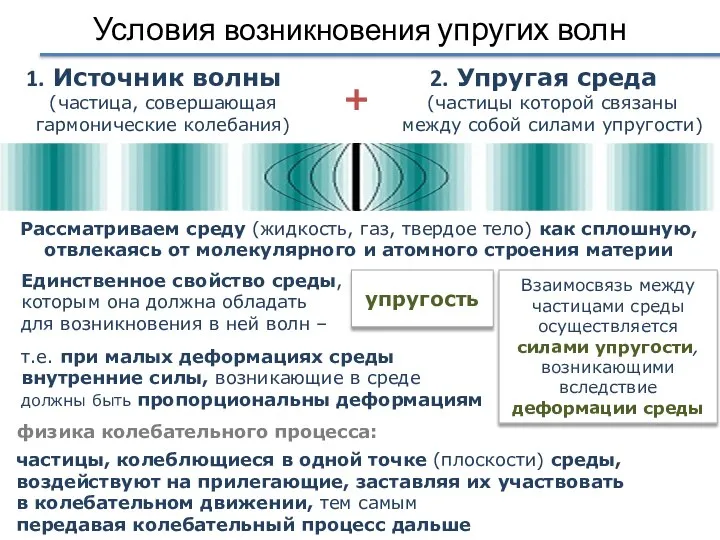
- 5. Условия возникновения упругих волн частицы, колеблющиеся в одной точке (плоскости) среды, воздействуют на прилегающие, заставляя их
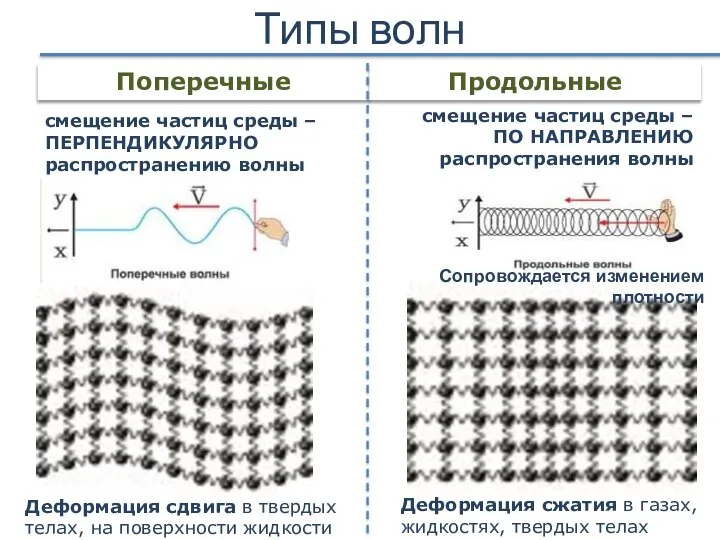
- 6. Типы волн Поперечные Продольные смещение частиц среды – ПО НАПРАВЛЕНИЮ распространения волны смещение частиц среды –ПЕРПЕНДИКУЛЯРНО
- 7. Распространение волн в средах Круговая волна на поверхности жидкости от точечного источника Генерация акустической волны громкоговорителем
- 8. Волны на поверхности жидкости Волны на поверхности жидкости не являются ни продольными, ни поперечными Если бросить
- 9. Упругие волны Взаимосвязь между частицами среды осуществляется силами упругости, возникающими вследствие деформации среды. При передаче колебаний
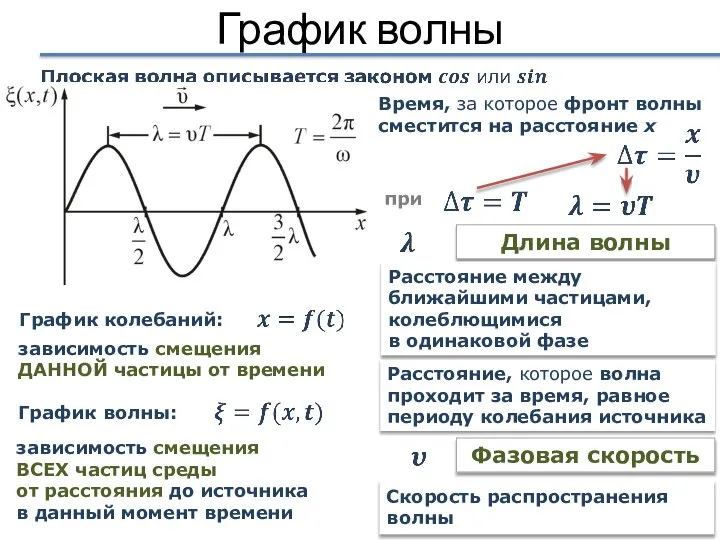
- 10. График волны График волны: График колебаний: зависимость смещения ДАННОЙ частицы от времени зависимость смещения ВСЕХ частиц
- 11. Волны в среде: определения Волновая (фазовая) поверхность геометрическое место точек, колеблющихся в одинаковой фазе Волновой фронт
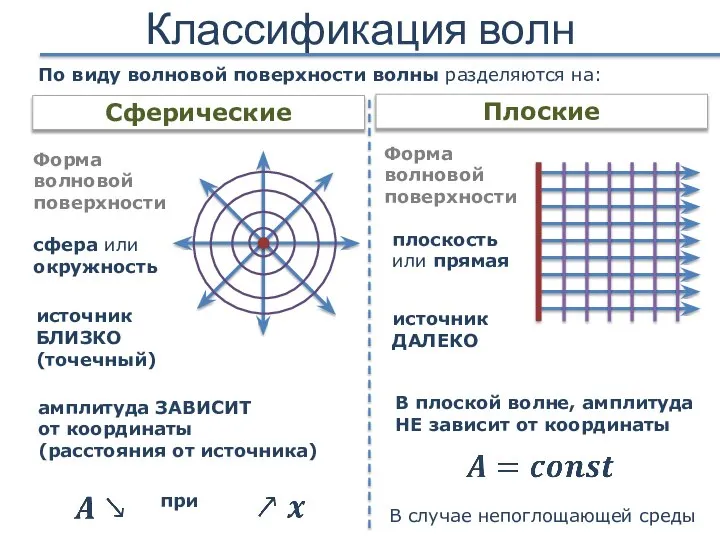
- 12. Классификация волн По виду волновой поверхности волны разделяются на: Сферические Плоские источник БЛИЗКО (точечный) источник ДАЛЕКО
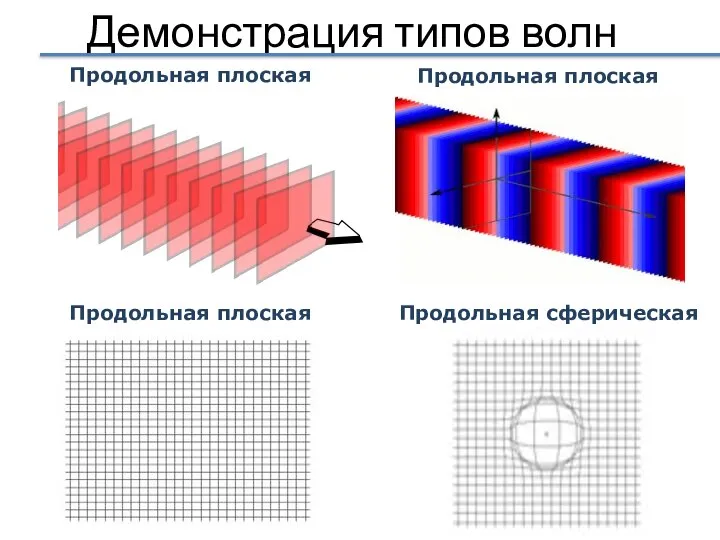
- 13. Демонстрация типов волн Продольная плоская Продольная сферическая Продольная плоская Продольная плоская
- 14. Уравнение бегущей волны волна, которая переносит в пространстве энергию Уравнение плоской бегущей волны в непоглощающей среде
- 15. Уравнение волны в поглощающей среде Уравнение плоской бегущей волны, распространяющейся в однородной изотропной непоглощающей среде в
- 16. Уравнение сферической волны Амплитуда колебаний убывает по закону Уравнение сферической волны в НЕпоглощающей среде Волновые поверхности
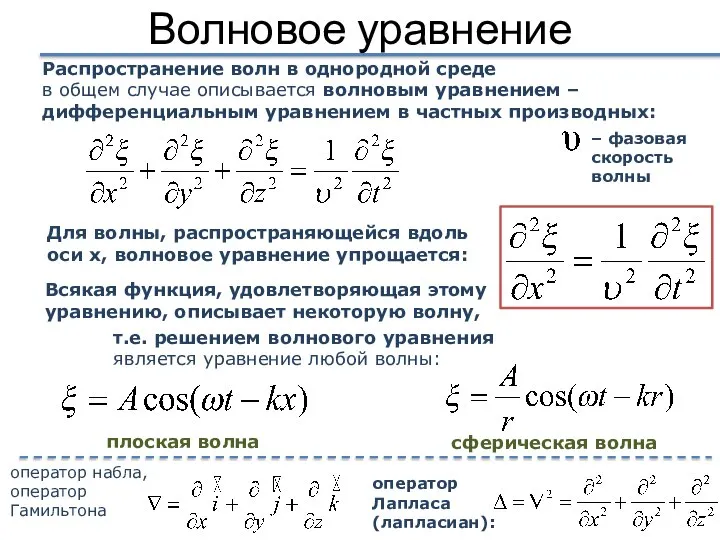
- 17. Дифференциальное волновое уравнение т.к. смещение частицы среды зависит не только от времени, но и от расстояния
- 18. Волновое уравнение Распространение волн в однородной среде в общем случае описывается волновым уравнением – дифференциальным уравнением
- 19. Перенос энергии бегущей волной Энергия волны в упругой среде состоит из кинетической энергии частиц, совершающих колебания
- 20. Плотность потенциальной энергии (энергия на единицу объема) Плотность кинетической энергии (энергия на единицу объема)
- 21. Средняя (за период) объемная плотность полной энергии
- 22. Энергия упругих волн Среда, в которой распространяется волна, обладает запасом энергии Количество энергии, переносимой волной через
- 23. Для монохроматической волны среднее по времени значение вектора Умова среднее по времени значение плотности потока энергии,
- 24. Николай Алексеевич Умов 23 января 1846 – 15 января 1915 Россия Русский физик и мыслитель 1875
- 25. Стоячие волны
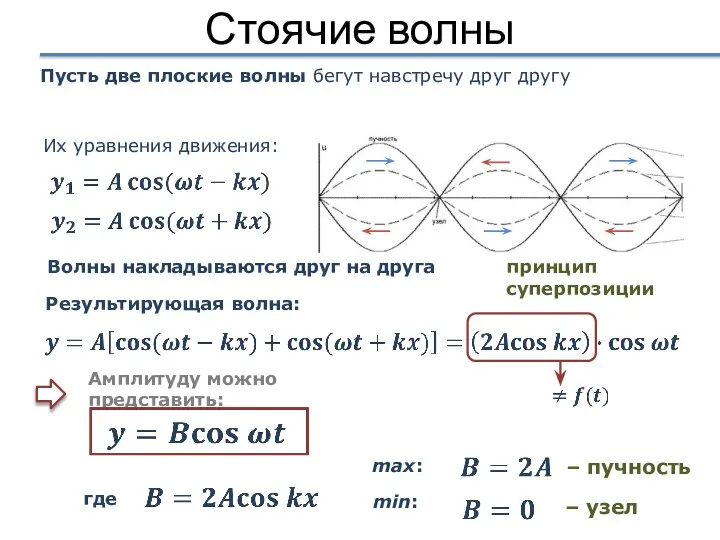
- 26. Стоячие волны Пусть две плоские волны бегут навстречу друг другу Их уравнения движения: Волны накладываются друг
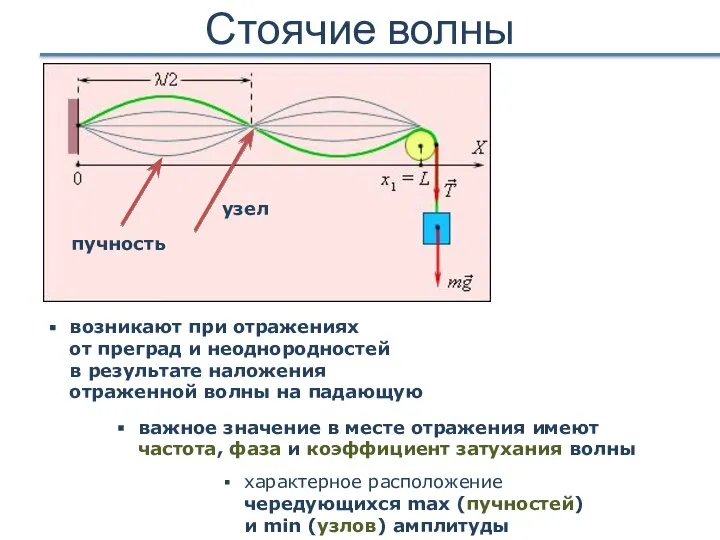
- 27. Стоячие волны характерное расположение чередующихся max (пучностей) и min (узлов) амплитуды возникают при отражениях от преград
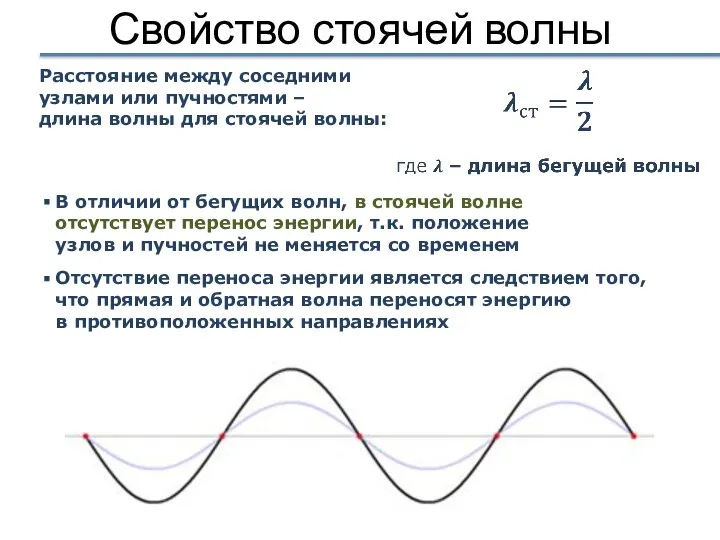
- 28. Свойство стоячей волны В отличии от бегущих волн, в стоячей волне отсутствует перенос энергии, т.к. положение
- 29. Образовавшаяся в результате интерференции волна является стоячей – через узлы энергия не переносится. Происходит превращение энергии
- 30. Координаты узлов и пучностей Найдем координаты узлов и пучностей Узлы: Пучности:
- 31. Стоячие волны в ограниченных средах Краевые условия: в точках закрепления струны или стержня, а также на
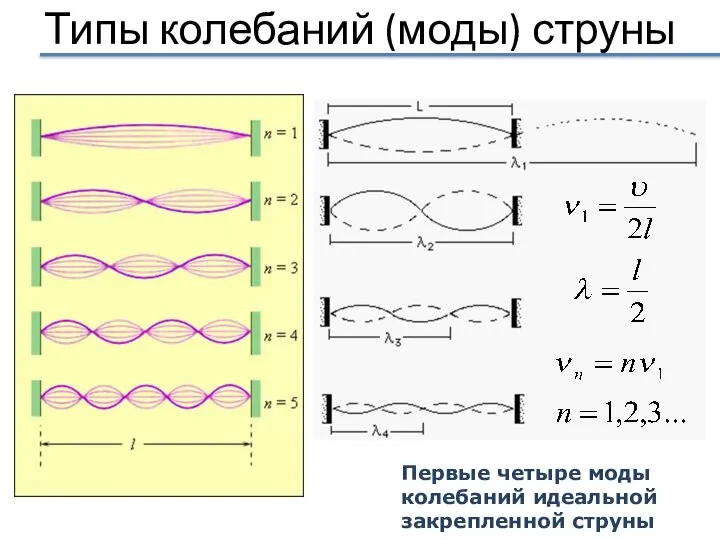
- 32. Типы колебаний (моды) струны Первые четыре моды колебаний идеальной закрепленной струны
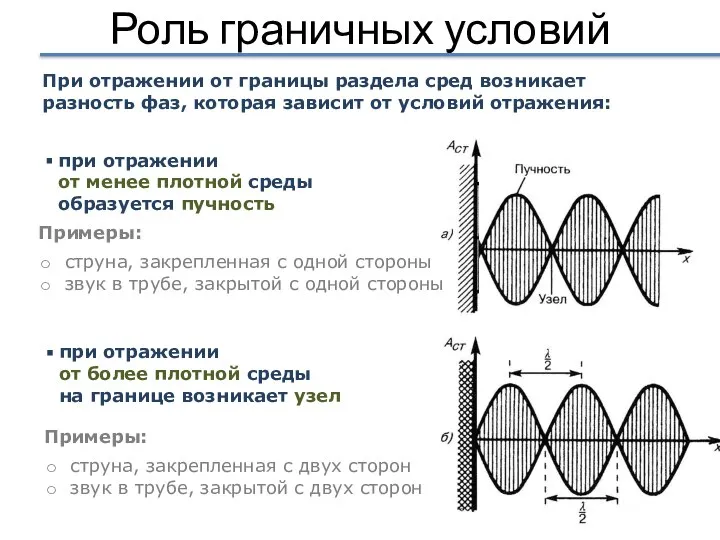
- 33. Роль граничных условий при отражении от более плотной среды на границе возникает узел При отражении от
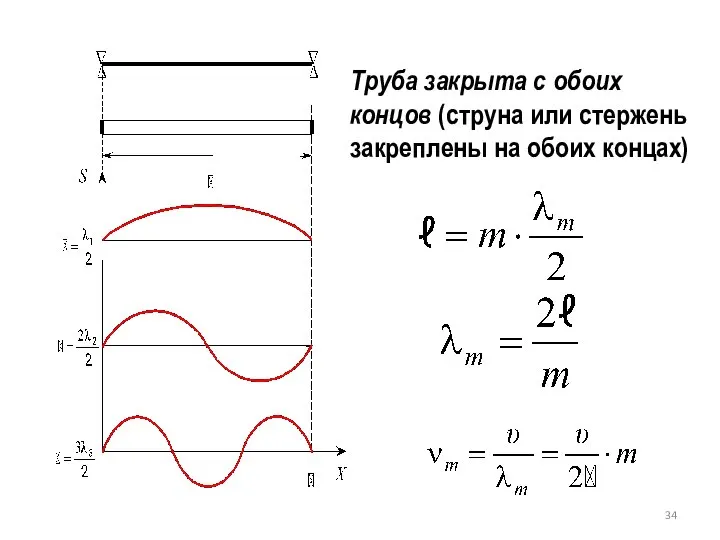
- 34. Труба закрыта с обоих концов (струна или стержень закреплены на обоих концах)
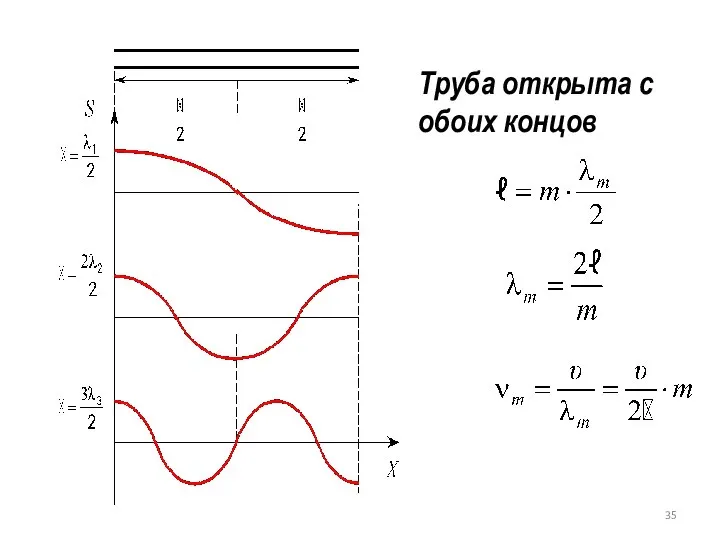
- 35. Труба открыта с обоих концов
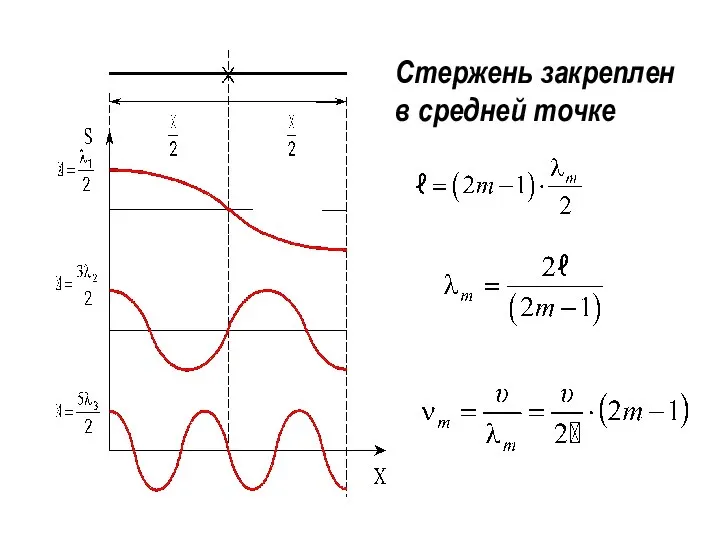
- 36. Стержень закреплен в средней точке
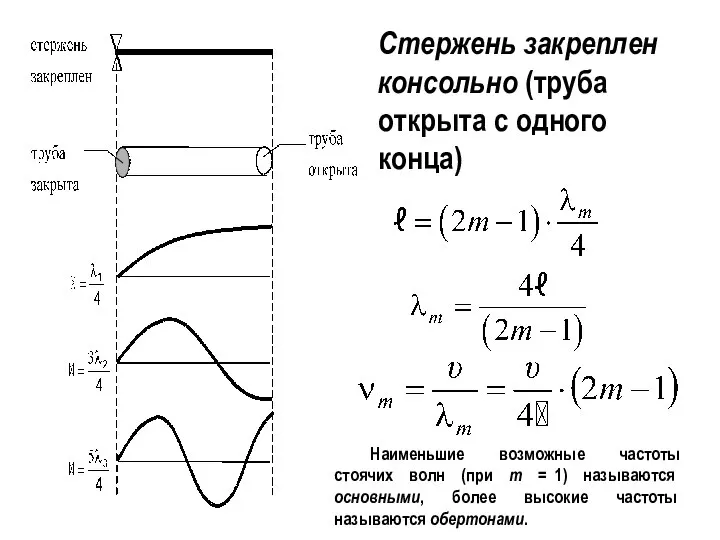
- 37. Стержень закреплен консольно (труба открыта с одного конца) Наименьшие возможные частоты стоячих волн (при m =
- 38. Электромагнитные волны
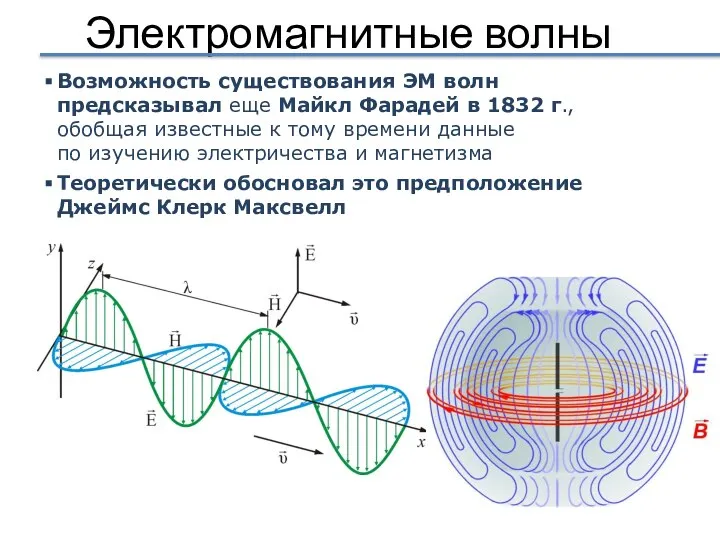
- 39. Электромагнитные волны Возможность существования ЭМ волн предсказывал еще Майкл Фарадей в 1832 г., обобщая известные к
- 40. Джеймс Клерк Максвелл (13 июня 1831 – 5 ноября 1879) Шотландия, Англия James Clerk Maxwell Кроме
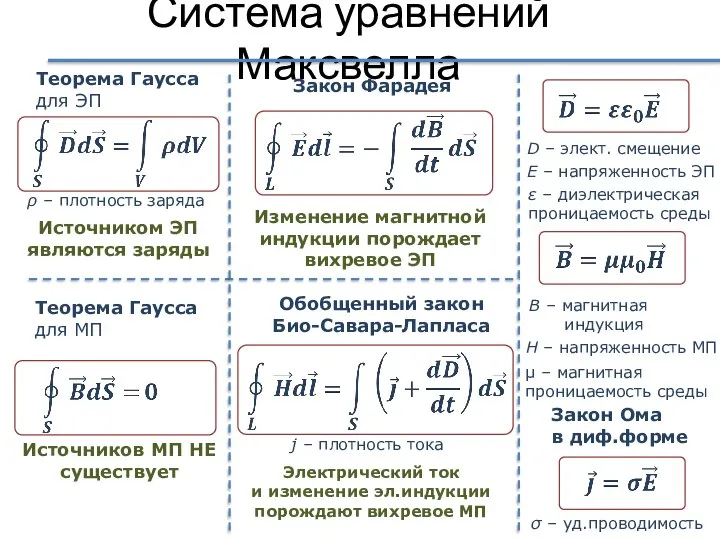
- 41. Система уравнений Максвелла Теорема Гаусса для МП Закон Фарадея ρ – плотность заряда Теорема Гаусса для
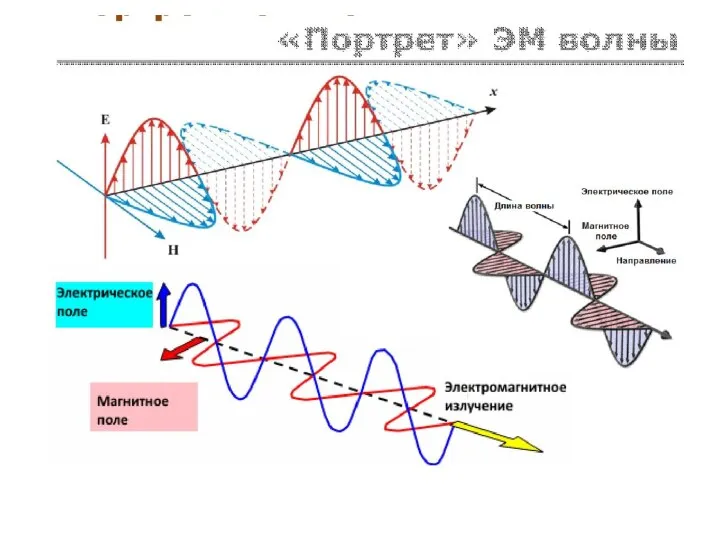
- 43. ЭМ волна и ее свойства 3. ЭМ волны – ПОПЕРЕЧНЫЕ волны 1. ЭМ волны излучаются движущимся
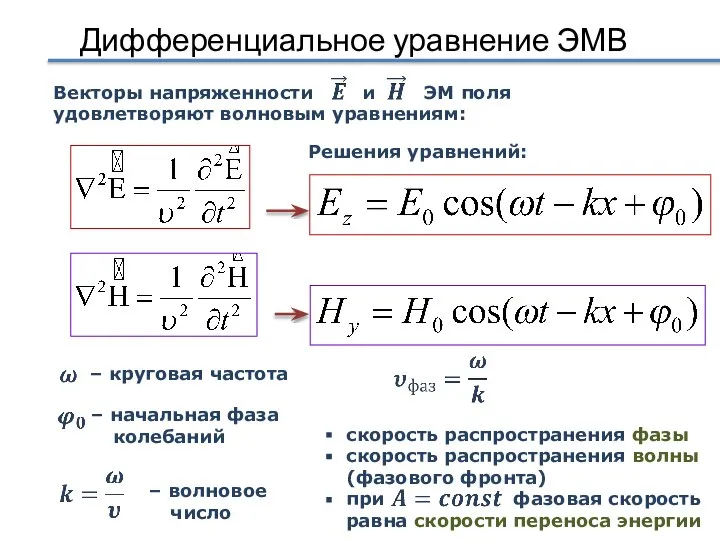
- 44. Дифференциальное уравнение ЭМВ Векторы напряженности и ЭМ поля удовлетворяют волновым уравнениям: Решения уравнений: – круговая частота
- 45. Скорость распространения ЭМ волн Скорость распространения ЭМ волн в среде зависит от электрических и магнитных свойств
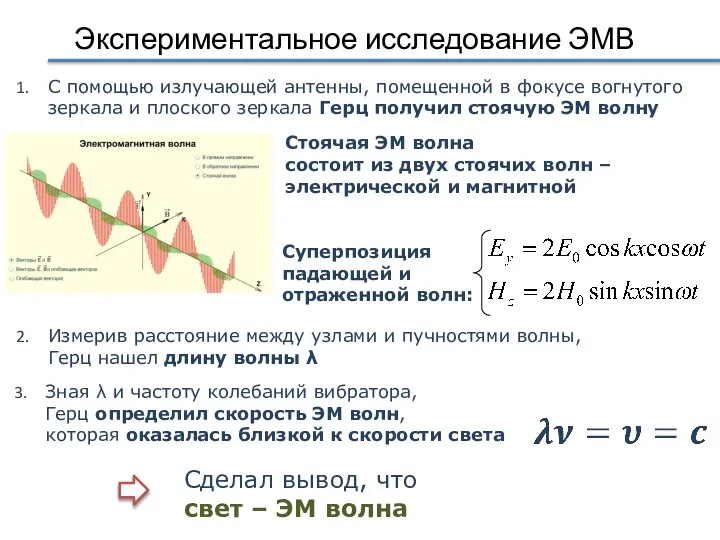
- 48. Экспериментальное исследование ЭМВ С помощью излучающей антенны, помещенной в фокусе вогнутого зеркала и плоского зеркала Герц
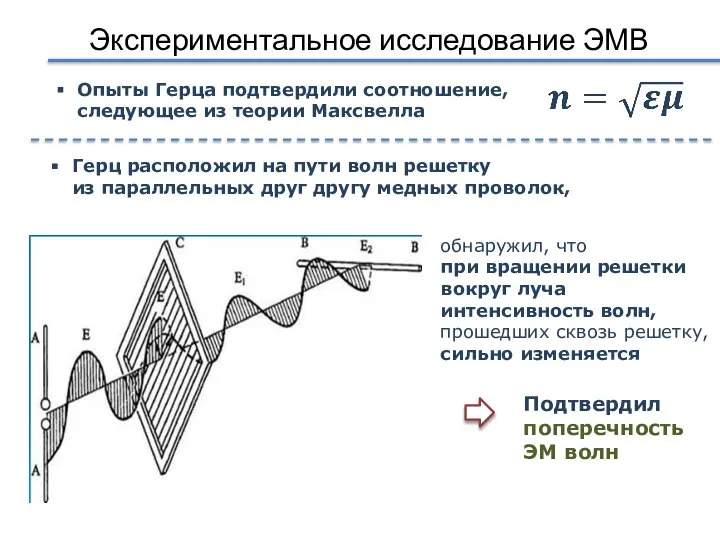
- 49. Экспериментальное исследование ЭМВ Опыты Герца подтвердили соотношение, следующее из теории Максвелла Подтвердил поперечность ЭМ волн Герц
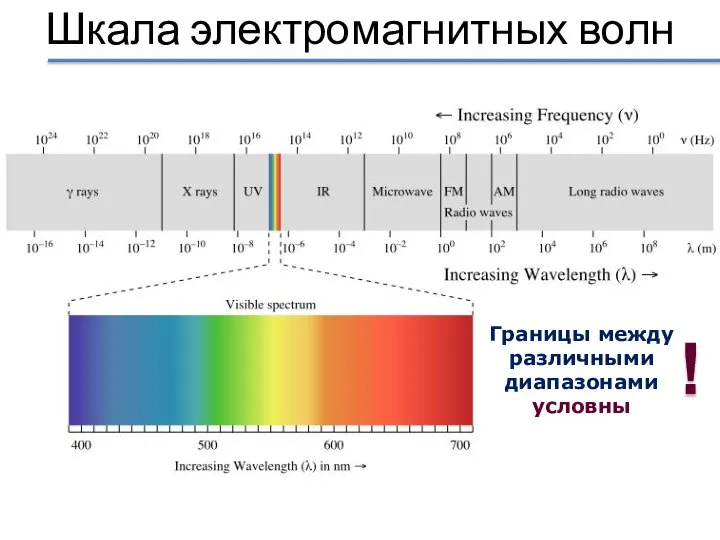
- 50. Шкала электромагнитных волн Границы между различными диапазонами условны !
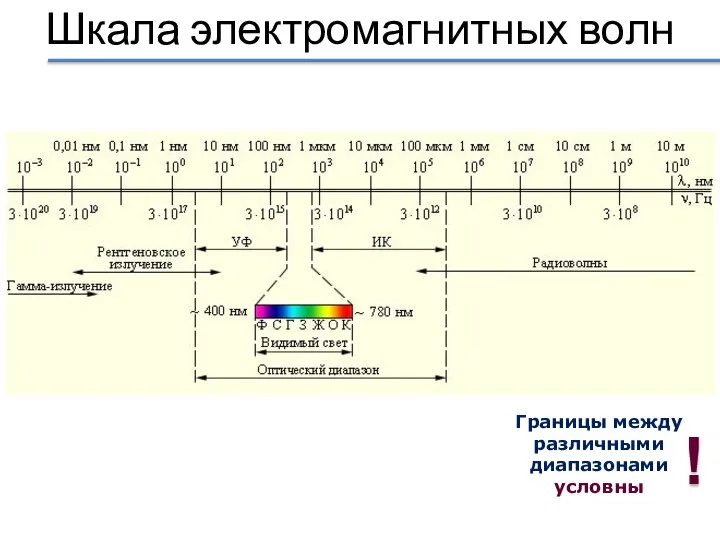
- 51. Шкала электромагнитных волн Границы между различными диапазонами условны !
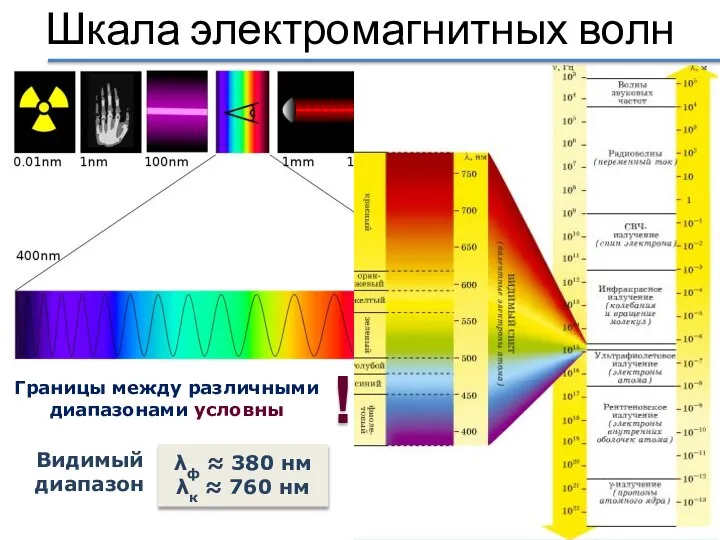
- 52. Шкала электромагнитных волн Границы между различными диапазонами условны ! λф ≈ 380 нм λк ≈ 760
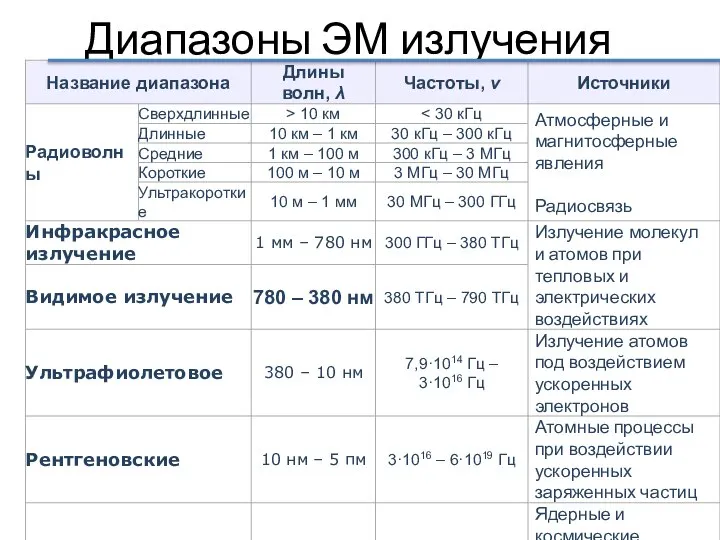
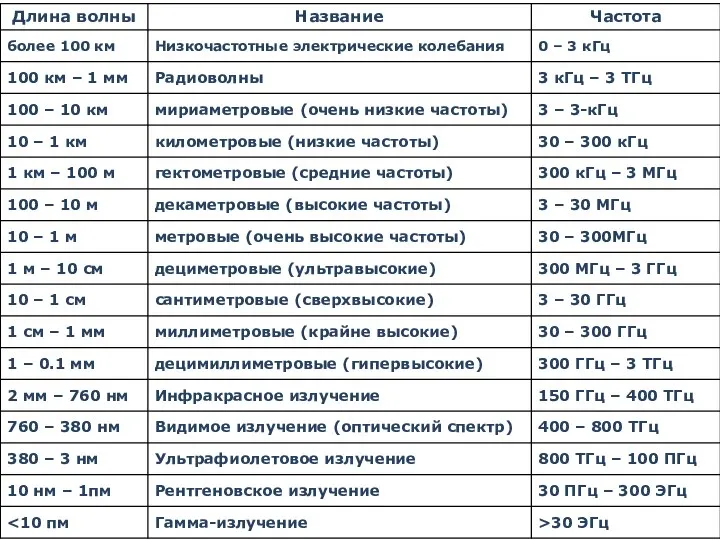
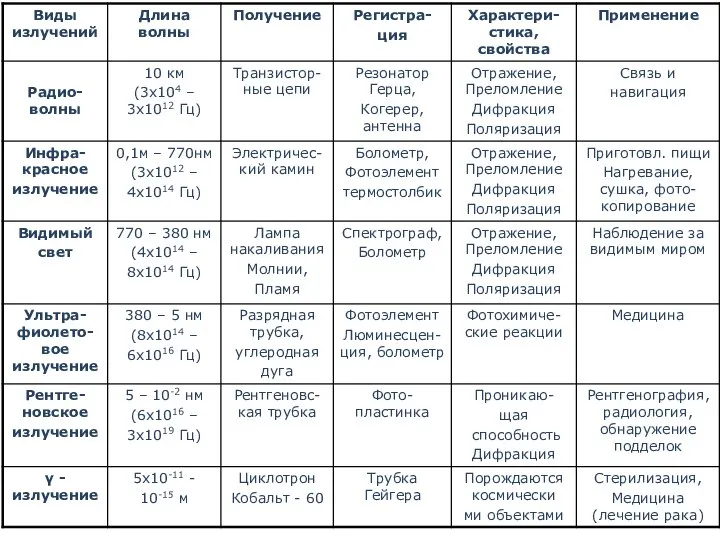
- 53. Диапазоны ЭМ излучения
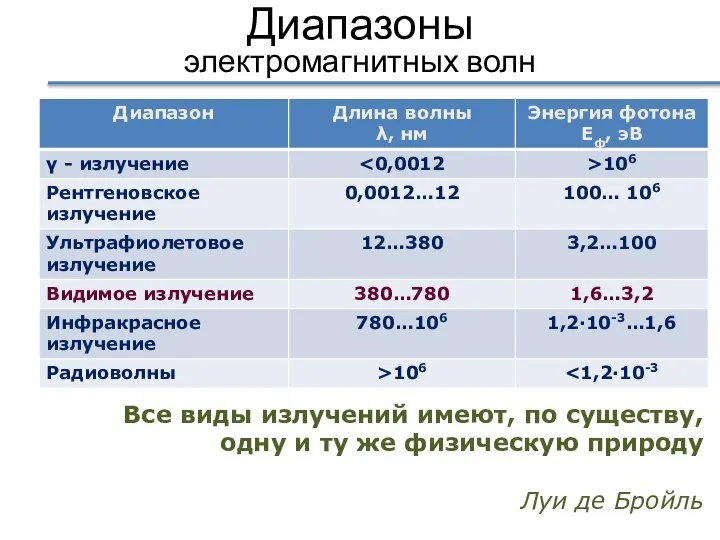
- 56. Диапазоны электромагнитных волн Все виды излучений имеют, по существу, одну и ту же физическую природу Луи
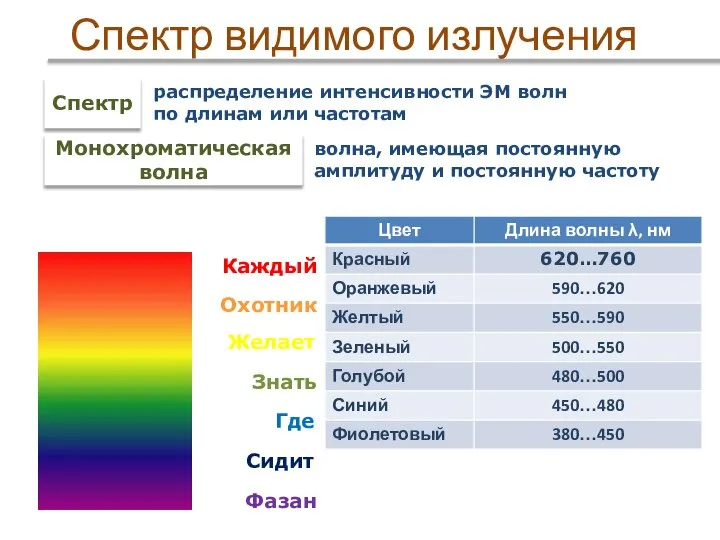
- 57. Спектр видимого излучения Каждый Охотник Желает Знать Где Сидит Фазан Спектр распределение интенсивности ЭМ волн по
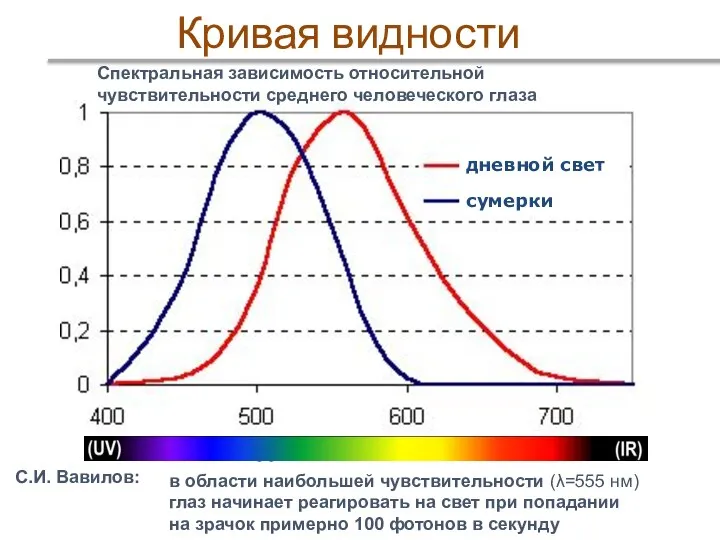
- 58. Кривая видности Спектральная зависимость относительной чувствительности среднего человеческого глаза дневной свет сумерки С.И. Вавилов: в области
- 59. Энергия и импульс ЭМ волны Распространение ЭМ волн связано с переносом энергии (подобно тому, как распространение
- 60. Джон Генри Пойнтинг 9 сентября 1852 – 30 марта 1914 Англия John Henry Poynting 1883 –
- 61. Вектор Умова-Пойнтинга Поток энергии за 1 с через единичную площадку (S=1м2), ⊥ направлению распространения волны: Объемная
- 62. ЭМ масса и импульс ЭМ полю присущи ЭМ импульс и масса
- 63. Эффект Доплера Соотношение, описывающее эффект Доплера для ЭМ волн в вакууме, с учетом преобразований Лоренца, имеет
- 64. Поперечный эффект Доплера Поперечный эффект значительно слабее Поперечный эффект Продольный эффект Впервые экспериментальная проверка существования эффекта
- 65. Применение эффекта Доплера Эффект Доплера нашел широкое применение в науке и технике, например на нем основаны:
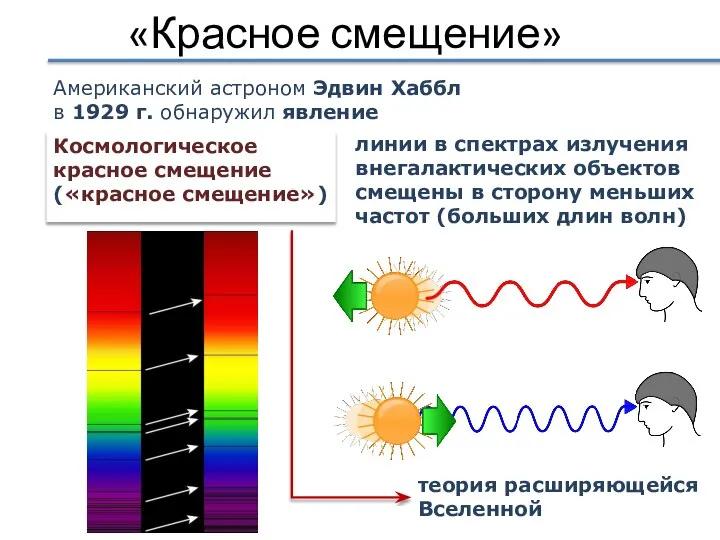
- 66. «Красное смещение» Американский астроном Эдвин Хаббл в 1929 г. обнаружил явление Космологическое красное смещение («красное смещение»)
- 67. Расширяющаяся Вселенная 65 млн. св. лет 325 млн. св. лет 4 млрд. св. лет Дева Персей
- 68. Расширяющаяся Вселенная «Красное смещение» - проявление эффекта Доплера В современные телескопы можно наблюдать часть Метагалактики, оптический
- 70. Скачать презентацию
































 Пузырьковая камера
Пузырьковая камера Вещества и явления в окружающем мире
Вещества и явления в окружающем мире Колебания математического и пружинного маятников
Колебания математического и пружинного маятников Паровая машина Ползунова
Паровая машина Ползунова Дополнительное оборудование
Дополнительное оборудование Автономные инверторы
Автономные инверторы T1klsAl4UwZclqq9KGDB6w
T1klsAl4UwZclqq9KGDB6w Сравнение эксплуатационных характеристик lada vestaи и lada xray
Сравнение эксплуатационных характеристик lada vestaи и lada xray Гальванические источники
Гальванические источники Сравнение сил. 7класс
Сравнение сил. 7класс Модели молекул простого и сложного вещества
Модели молекул простого и сложного вещества Гидродинамика. Движение жидкости
Гидродинамика. Движение жидкости Особенности гидродинамики потока во входном участке активной зоны реактора PWR с тепловыделяющими сборками ТВС-Квадрат
Особенности гидродинамики потока во входном участке активной зоны реактора PWR с тепловыделяющими сборками ТВС-Квадрат Работа, мощность и энергия
Работа, мощность и энергия Недомолвки в теории и недостатки в практике регистрации частичных разрядов
Недомолвки в теории и недостатки в практике регистрации частичных разрядов Полупроводниковые лазеры, их особенности
Полупроводниковые лазеры, их особенности Космология Ньютона. Часть 2. Физика космоса
Космология Ньютона. Часть 2. Физика космоса Напряжения в эллиптической оболочке, соединенной с цилиндром
Напряжения в эллиптической оболочке, соединенной с цилиндром Сцепление ГАЗ 53-12. Урок №70
Сцепление ГАЗ 53-12. Урок №70 Презентация на тему: основы термодинамики
Презентация на тему: основы термодинамики Автомобили III
Автомобили III Виды ионизирующего излучения и основные понятия дозиметрии
Виды ионизирующего излучения и основные понятия дозиметрии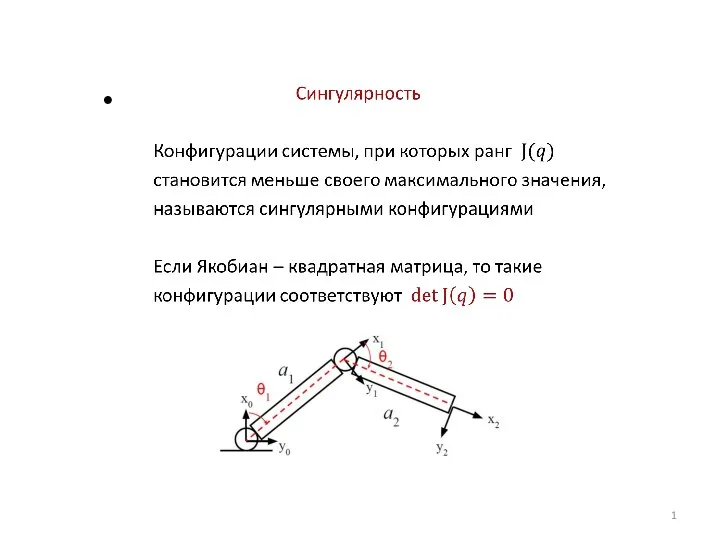 Сингулярность. Сингулярные конфигурации
Сингулярность. Сингулярные конфигурации Давление газа
Давление газа Дирижаблестроение. Тема № 1
Дирижаблестроение. Тема № 1 Криволинейное движение. Движение тела по окружности
Криволинейное движение. Движение тела по окружности Внутренняя энергия
Внутренняя энергия Колесный бульдозер
Колесный бульдозер