Содержание
- 2. 1. Основные теоремы динамики точки Основные теоремы динамики: Теорема об изменении количества движения материальной точки Теорема
- 3. 2. Теорема об изменении количества движения равно Элементарное изменение количества движения материальной точки элементарному импульсу силы,
- 4. 3. Первые интегралы Случай 1 При отсутствии силы свободная материальная точка движется равномерно и прямолинейно Случай
- 5. 4. Первые интегралы В общем случае при вычислении импульса нужно знать , т.е. решение уравнений движения.
- 6. 5. Теорема об изменении момента количества движения Момент количества движения точки M относительно точки О равен
- 7. 6. Теорема об изменении момента количества движения Теорема об изменении момента количества движения в проекциях на
- 8. 7. Первые интегралы в случае центральной силы Это возможно или когда сила F = 0, или
- 9. Так как вектор перпендикулярный к плоскости, проходящей через векторы r и v, имеет постоянное направление, то
- 10. Секторная скорость характеризует скорость изменения площади поверхности, описываемой радиус вектором 9. Следствие 2 секторная скорость 2-ой
- 11. 10. Теорема об изменении кинетической энергии Скалярная величина T, равная половине произведения массы точки на квадрат
- 12. 11. Работа силы Представление работы в виде криволинейного интеграла 1-го рода Элементарная работа Представление работы в
- 13. 12. Теорема об изменении КЭ в терминах работы Связь между работой и мощностью мощность равна работе,
- 14. 13. Пример 1: постоянная сила Для силы тяжести имеем + если М опускается - если М
- 15. 14. Пример 2 В общем случае работа силы зависит не только от начального и конечного положений
- 16. 15. Задачи, решаемые с помощью Т. об изменении энергии С помощью теоремы об изменении кинетической энергии
- 18. Скачать презентацию















 Закон Кулона
Закон Кулона Классификация кристаллов на металлы, полупроводники и диэлектрики с точки зрения зонной теории
Классификация кристаллов на металлы, полупроводники и диэлектрики с точки зрения зонной теории Зенкерование и развертывание отверстий
Зенкерование и развертывание отверстий Ядерное оружие
Ядерное оружие Технологические характеристики грунтов. Определение трудности процессов разработки горных пород
Технологические характеристики грунтов. Определение трудности процессов разработки горных пород Расчет сопротивления электрических цепей
Расчет сопротивления электрических цепей Строение атома. Опыты Резерфорда
Строение атома. Опыты Резерфорда Эксперименты с использованием датчиков температуры
Эксперименты с использованием датчиков температуры Оптика и квантовая физика. Лекция 12
Оптика и квантовая физика. Лекция 12 Поляризация диэлектриков
Поляризация диэлектриков Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики Простые механизмы
Простые механизмы Электричество и магнетизм (лекция 11)
Электричество и магнетизм (лекция 11) Электрический ток
Электрический ток 6. Механика жидкости и газа.ppt
6. Механика жидкости и газа.ppt Презентация на тему Поверхностное натяжение жидкостей
Презентация на тему Поверхностное натяжение жидкостей 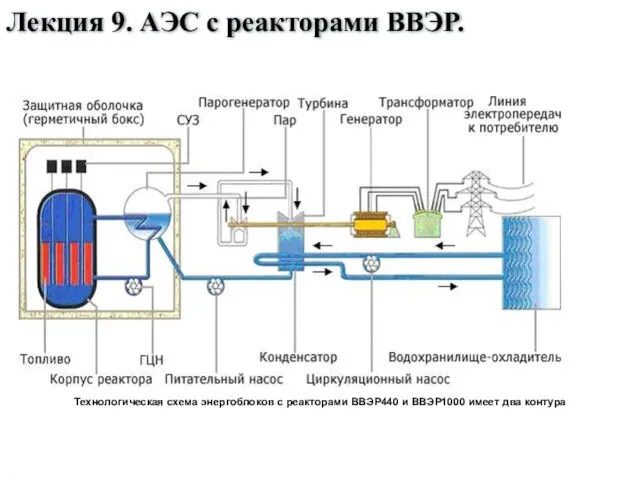 АЭС с реакторами ВВЭР. Лекция 9
АЭС с реакторами ВВЭР. Лекция 9 Презентация на тему Закон преломления света (8 класс)
Презентация на тему Закон преломления света (8 класс)  Манометры поршневой жидкостный насос. Гидравлический пресс (7 класс)
Манометры поршневой жидкостный насос. Гидравлический пресс (7 класс) Движение тела по окружности
Движение тела по окружности Центр тяжести.Виды равновесия (10 класс)
Центр тяжести.Виды равновесия (10 класс) Электрический ток в жидкостях
Электрический ток в жидкостях Критическое состояние вещества, опыт Авенариуса
Критическое состояние вещества, опыт Авенариуса Электромагнитные излучения
Электромагнитные излучения Обледенение летательных аппаратов
Обледенение летательных аппаратов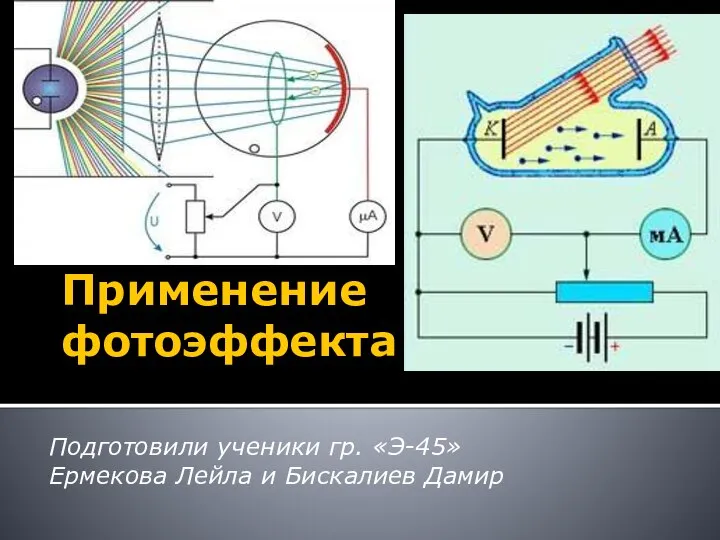 Применение фотоэффекта
Применение фотоэффекта Презентация на тему Освещение
Презентация на тему Освещение  Презентация на тему Электростатика Лекция
Презентация на тему Электростатика Лекция