Кинематика_ _Лекция 1_ (1)

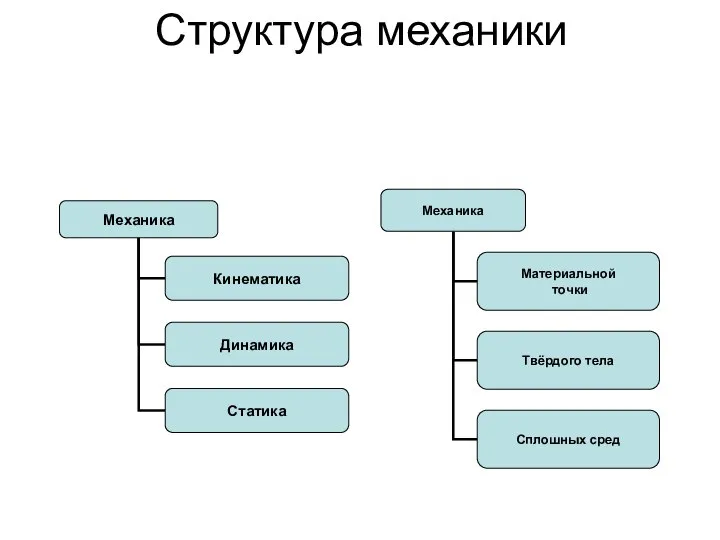
Структура механики

Основные понятия механики
Основная задача механики – зная состояние системы в начальный момент времени и законы, управляющие движением, определить состояние системы во все последующие моменты времени. Эта задача не может быть решена точно
Кинематика – это раздел физики, посвящённый изучению движения тел. При этом причины движения не рассматриваются

Кинематика - наука, изучающая состояние движения независимо от вызывающих его сил, и получившая название от греческого слова
kinematos (-состояние движения) и составляющая часть общей науки о движении -механики. Цель ее состоит в изучении геометрических свойств движения, скоростей и ускорений: для достижения этой цели пользуются анализом и геометрией.
Кинематика

Кинематику называют геометрией четырех измерений, так как она имеет дело с тремя координатами пространства и еще с четвертым переменным,представляющим собой время.
Скорости представляются первыми производными от координаты по времени,
ускорение - вторыми производными и еще, кроме того, рассматриваются производные от координат по времени высших порядков, называемые ускорениями высших порядков. С аналитической точки зрения, вся кинематика сводится к изучению соотношений, существующих между этими величинами.

Некоторые сведения о векторах
Вектором будем называть величину, характеризующуюся численным значением (модулем) и направлением в пространстве, для которой задан закон сложения (правило параллелограмма)

Векторы и скаляры.
Величины, которые полностью определяются только числовыми значениями, называются скалярами.
Величины, для полной характеристики которых нужно знать не только их величину, но и направление – векторы.
В физике широко применяется векторная форма описания движения. Положение точки задается радиус – вектором это вектор, проведенный из начала координат в данную точку .
Для любого действия над произвольными векторами нужно предварительно перенести один из векторов параллельно самому себе так, чтобы векторы выходили из одной точки. Если векторов несколько, действия производят попарно, или берут проекции на две взаимно перпендикулярные оси (х и y).

Сложение векторов можно осуществлять несколькими способами.
1. правило треугольника
Используя правило треугольника при сложении векторов А и В, перенесем вектор В параллельно самому себе, чтобы его начало оказалось совмещенным с концом вектора А. Тогда вектор С, проведенный из начала вектора А в конец вектора В, будет представлять собой результирующий вектор: С=А+В.
Сложение векторов

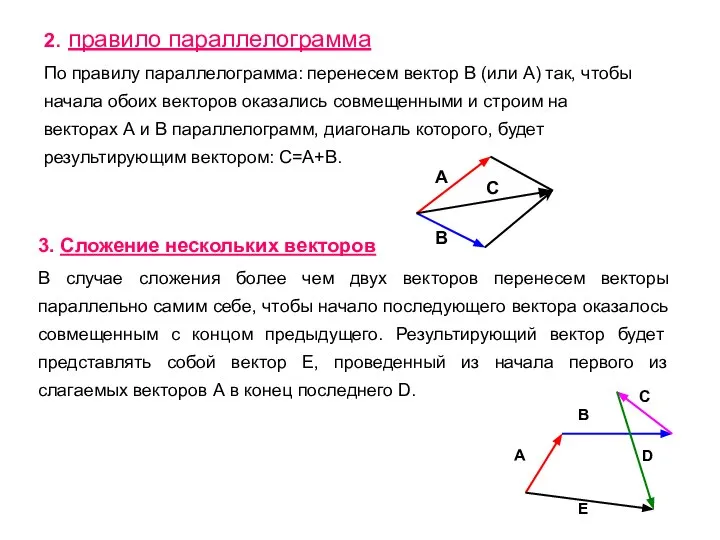
2. правило параллелограмма
По правилу параллелограмма: перенесем вектор В (или А) так, чтобы начала обоих векторов оказались совмещенными и строим на векторах А и В параллелограмм, диагональ которого, будет результирующим вектором: С=А+В.
3. Сложение нескольких векторов
В случае сложения более чем двух векторов перенесем векторы параллельно самим себе, чтобы начало последующего вектора оказалось совмещенным с концом предыдущего. Результирующий вектор будет представлять собой вектор Е, проведенный из начала первого из слагаемых векторов А в конец последнего D.

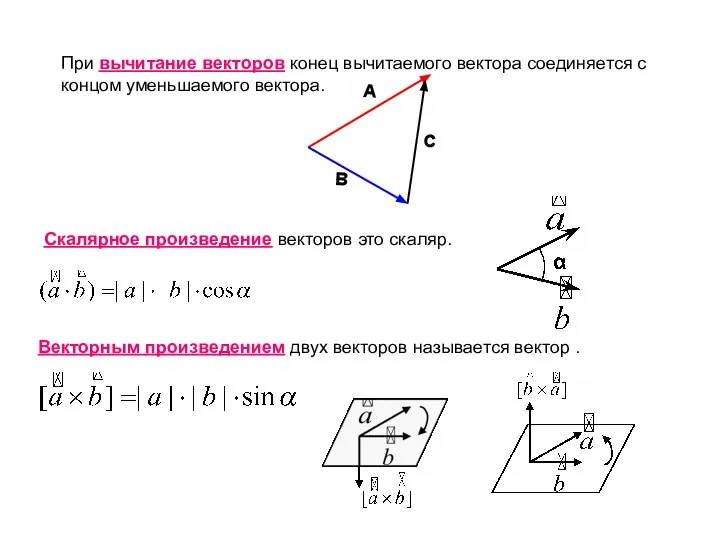
При вычитание векторов конец вычитаемого вектора соединяется с концом уменьшаемого вектора.
Скалярное произведение векторов это скаляр.
Векторным произведением двух векторов называется вектор .

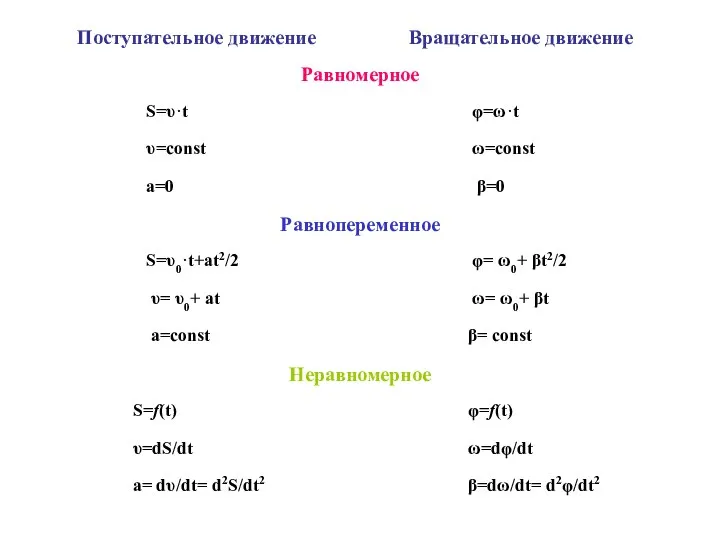
Основные понятия механики
Поступательное движение – такое, при котором любая прямая, связанная с телом перемещается параллельно самой себе
Вращательное движение – такое, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения

Кинематика поступательного движения
При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.

Основные понятия кинематики
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени

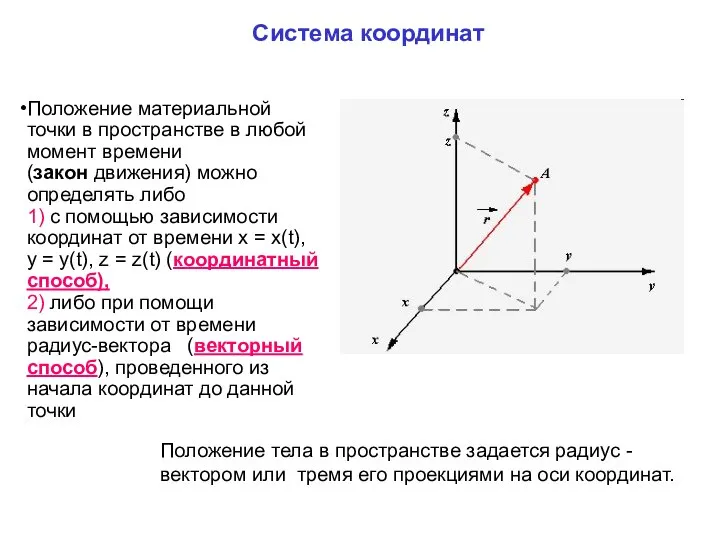
Система координат состоит из осей, для определения пространственных координат тела и часов
Траектория – это линия, которую описывает некоторая материальная точка в процессе движения
Путь – это расстояние между двумя точками, измеренное вдоль траектории движения

Рассмотрение любого движения начинают с выбора системы отсчета, включающей в себя:
тело отсчета,
систему координат и
приборы для исследования движения.

Тело отсчёта
Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени. В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.

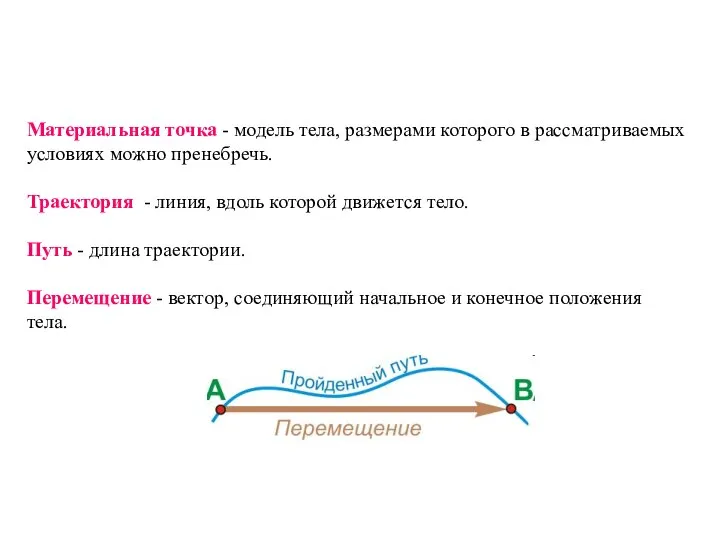
Материальная точка - модель тела, размерами которого в рассматриваемых условиях можно пренебречь.
Траектория - линия, вдоль которой движется тело.
Путь - длина траектории.
Перемещение - вектор, соединяющий начальное и конечное положения тела.

Положение тела в пространстве задается радиус - вектором или тремя его проекциями на оси координат.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо
1) с помощью зависимости координат от времени x = x(t), y = y(t), z = z(t) (координатный способ),
2) либо при помощи зависимости от времени радиус-вектора (векторный способ), проведенного из начала координат до данной точки
Система координат

Следовательно закон движения - это зависимость радиус-вектора от времени или зависимость координат во времени.
где - радиус-вектор, x, y, z - координаты тела.

Средняя скорость и её модуль
Для характеристики движения вводится понятие средней скорости
Средней скоростью называется величина, равная отношению перемещения тела ∆S за некоторый промежуток времени ∆t к этому промежутку
Модуль средней скорости определяется как отношение пути ∆S, пройденного телом за некоторый промежуток времени, к этому промежутку

Мгновенная скорость
При неограниченном уменьшении времени ∆t, скорость V стремится к предельному значению, которое называется мгновенной скоростью. Итак, мгновенная скорость v есть величина, равная отношению очень малого перемещения к промежутку времени, в течение которого это перемещение произошло.
Направление вектора мгновенной скорости совпадает с направлением перемещения.

Для характеристики движения тела вводятся следующие понятия:
1) средняя скорость: .
Вектор V совпадает по направлению с Δr.
2) мгновенная скорость: скорость в заданный момент времени.
это вектор, всегда направленный по касательной к данной точке траектории.
Скорость можно определить как производную радиуса – вектора движущейся точки по времени:
Направление вектора скорости задается косинусами:
где α , β , γ -углы между вектором скорости и осями x, y, z соответственно.
Модуль мгновенной скорости определяется равенством:
где Vx , Vy , Vz - проекции вектора скорости на
координатные оси x, y, z

Равнопеременным называется движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково, т.е. на равные величины. Это движение может быть
равноускоренным и
равнозамедленным.

3) Ускорение – векторная физическая величина, характеризующая изменения скорости со временем, как по модулю, так и по направлению:
При криволинейном движении ускорение a представляют как сумму нормального и тангенциального ускорений: at + an.
среднее ускорение
мгновенное ускорение

Равномерное прямолинейное движение.
Равномерное движение - движение при котором материальная точка за любые равные промежутки времени совершает равные перемещения.
При равномерном прямолинейном движении скорость тела постоянна, ускорение равно нулю. Траектория равномерного прямолинейного движения - прямая линия.
Для физических величин характеризующих движение имеем:
a=0
V=Const
Sx = Vx· t
x=x0+ Vx·t

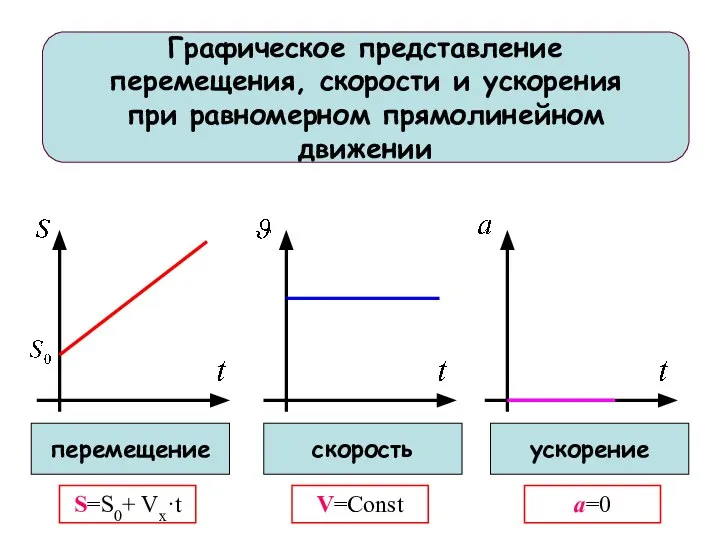
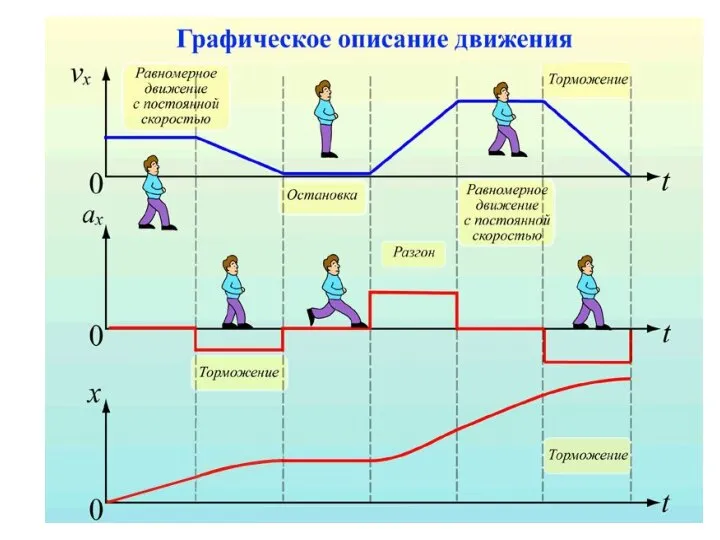
Графическое представление
перемещения, скорости и ускорения
при равномерном прямолинейном движении
перемещение
скорость
ускорение
S=S0+ Vx·t
V=Const
a=0

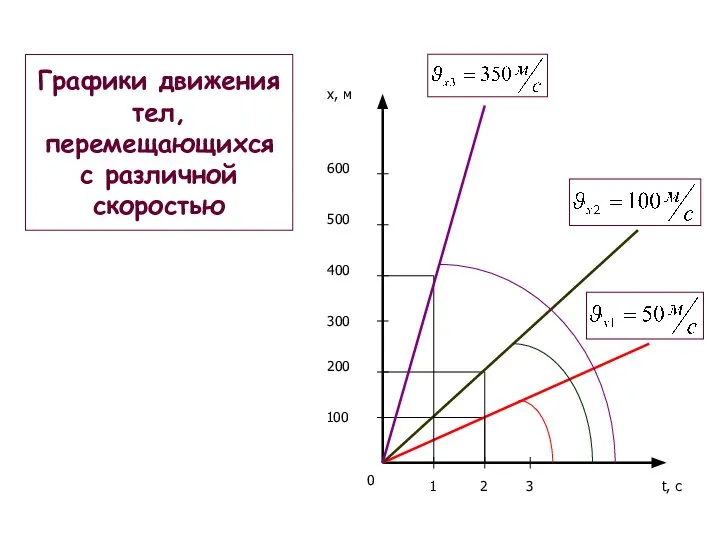
Графики движения тел, перемещающихся с различной скоростью
0
1
2
3
t, с
100
200
300
400
500
600
x, м

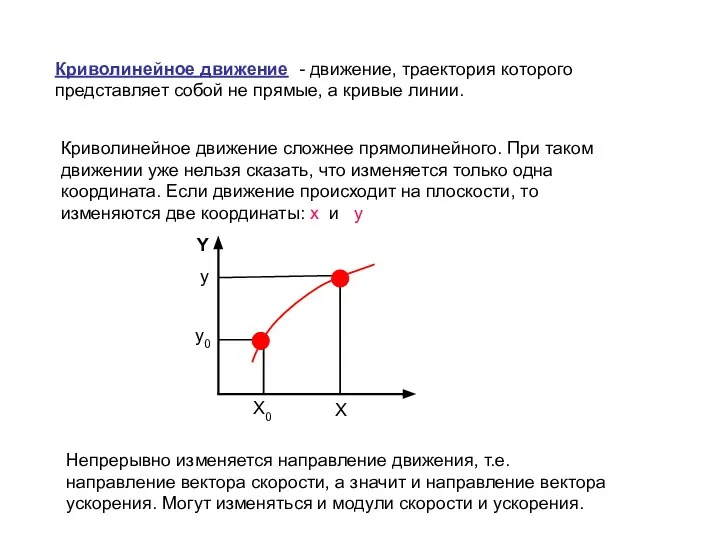
Криволинейное движение - движение, траектория которого представляет собой не прямые, а кривые линии.
Криволинейное движение сложнее прямолинейного. При таком движении уже нельзя сказать, что изменяется только одна координата. Если движение происходит на плоскости, то изменяются две координаты: x и y
Непрерывно изменяется направление движения, т.е. направление вектора скорости, а значит и направление вектора ускорения. Могут изменяться и модули скорости и ускорения.
Y
X0
y0
y
X

Неравномерное движение
Движение, при котором за равные промежутки времени тело совершает неравные перемещения называют неравномерным или переменным.

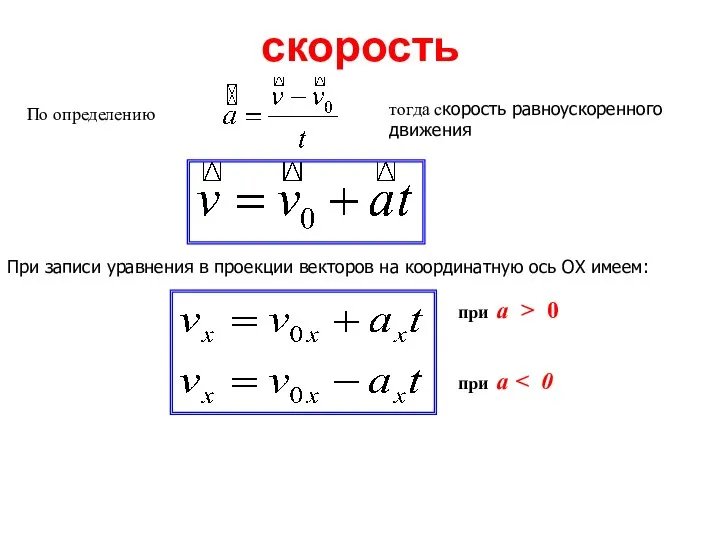
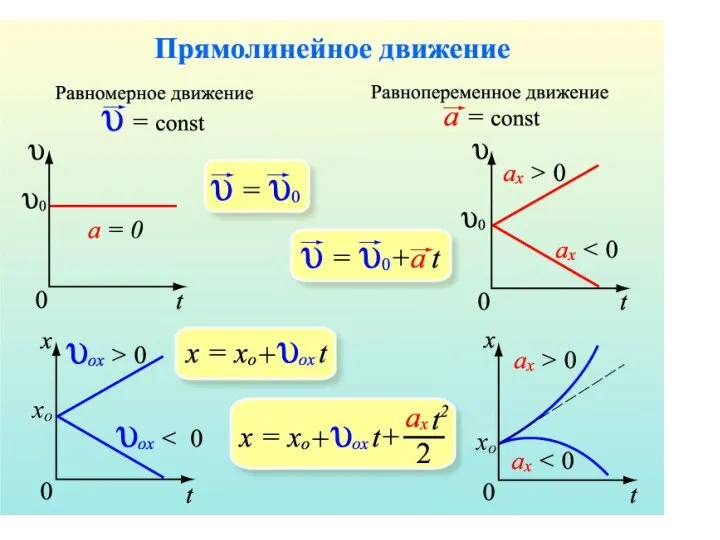
скорость
По определению
тогда скорость равноускоренного движения
При записи уравнения в проекции векторов на координатную ось ОХ имеем:
при a > 0
при a < 0

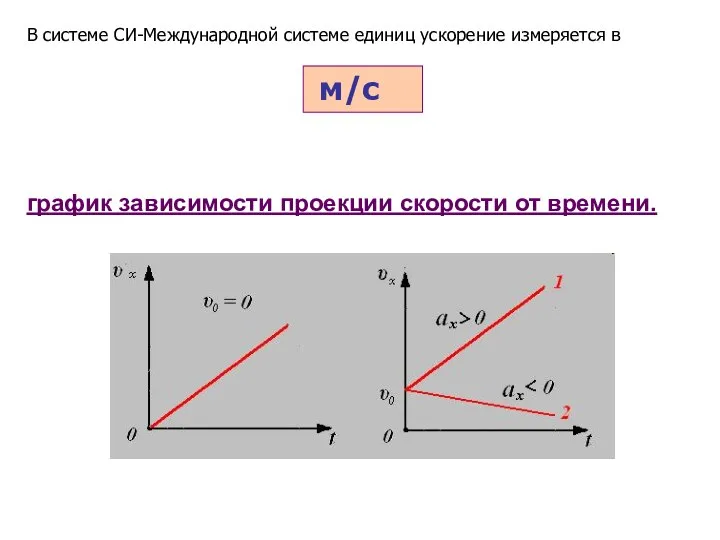
график зависимости проекции скорости от времени.
м/с
В системе СИ-Международной системе единиц ускорение измеряется в

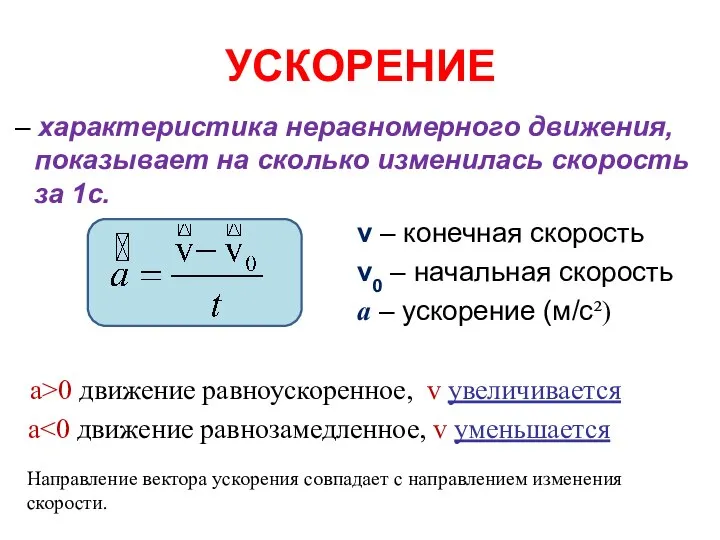
УСКОРЕНИЕ
– характеристика неравномерного движения, показывает на сколько изменилась скорость за 1с. v – конечная скорость
v0 – начальная скорость
а – ускорение (м/с²)
а>0 движение равноускоренное, v увеличивается
a<0 движение равнозамедленное, v уменьшается
Направление вектора ускорения совпадает с направлением изменения скорости.

график зависимости проекции ускорения от времени.
В системе СИ-Международной системе единиц ускорение измеряется в
м/с2
1 м/с2 - ускорение прямолинейно и равноускоренно движущейся точки, при котором за 1с ее скорость изменяется на 1м/с.

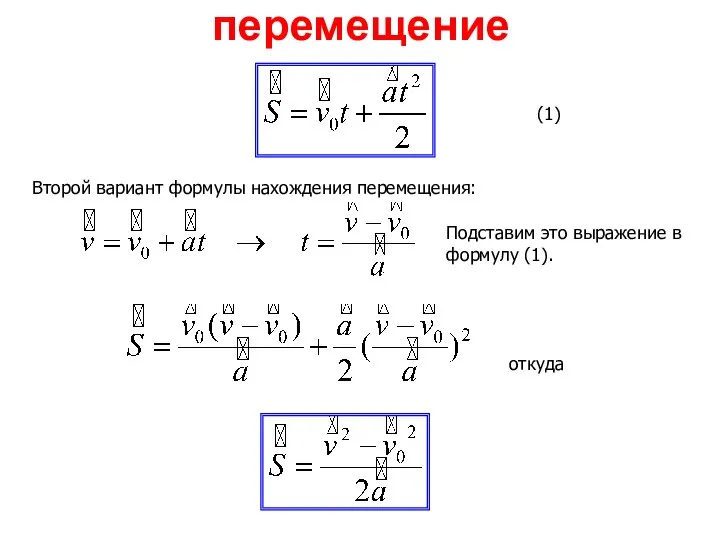
перемещение
Второй вариант формулы нахождения перемещения:
(1)
Подставим это выражение в формулу (1).
откуда

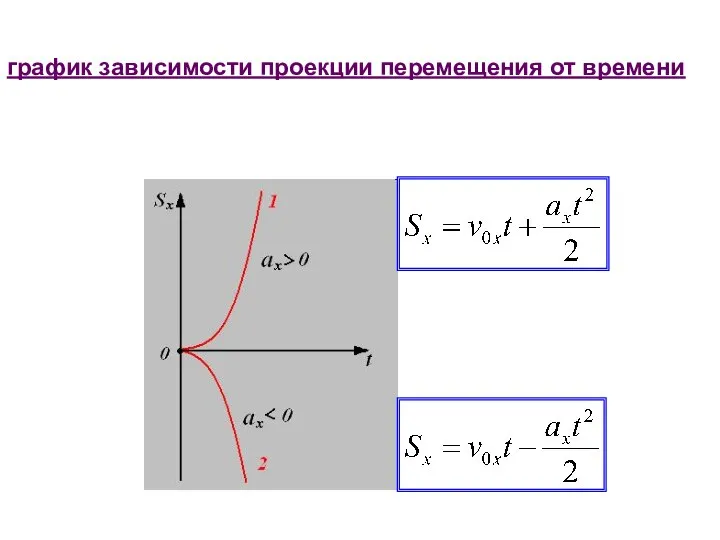
график зависимости проекции перемещения от времени

координата
график зависимости координаты от времени.
в любой момент времени для тела, движущегося равноускоренно
Проекция перемещения Sx =х-х0 , тогда

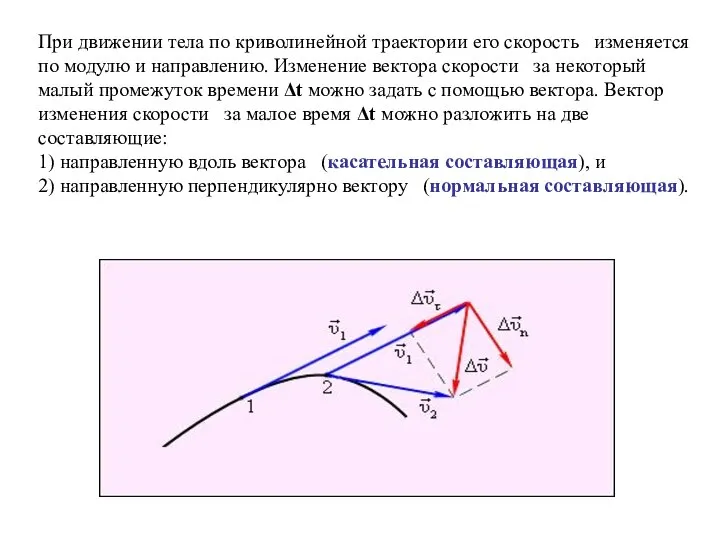
При движении тела по криволинейной траектории его скорость изменяется по модулю и направлению. Изменение вектора скорости за некоторый малый промежуток времени Δt можно задать с помощью вектора. Вектор изменения скорости за малое время Δt можно разложить на две составляющие:
1) направленную вдоль вектора (касательная составляющая), и
2) направленную перпендикулярно вектору (нормальная составляющая).

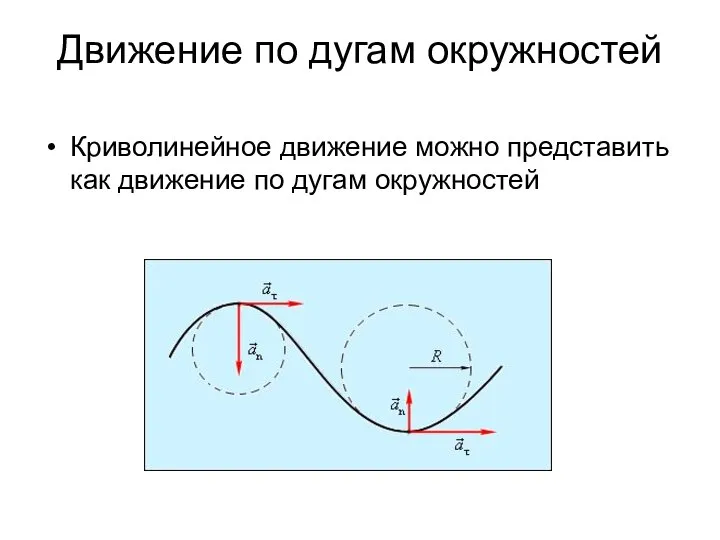
Движение по дугам окружностей
Криволинейное движение можно представить как движение по дугам окружностей

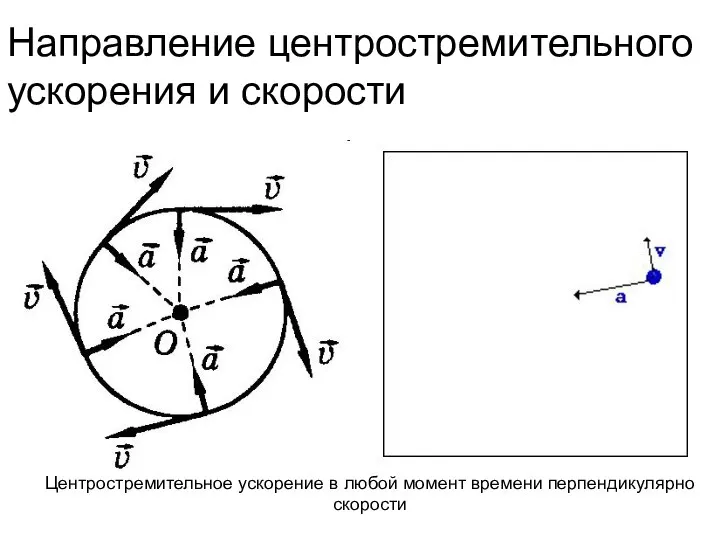
Направление центростремительного ускорения и скорости
Центростремительное ускорение в любой момент времени перпендикулярно скорости

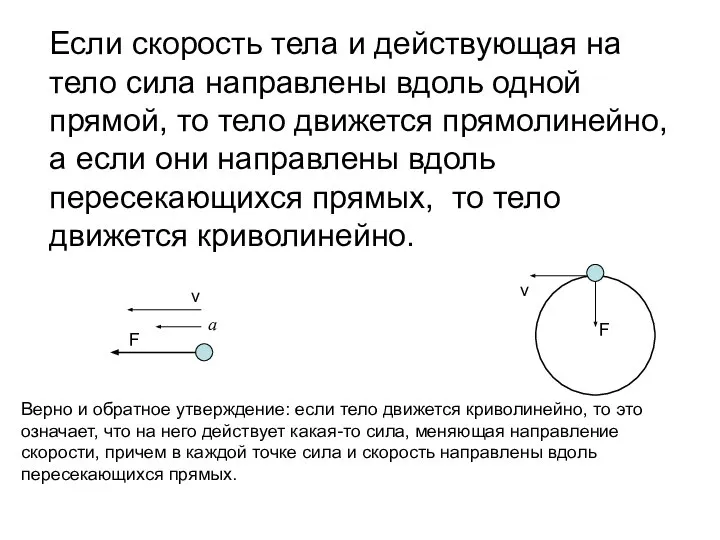
Если скорость тела и действующая на тело сила направлены вдоль одной прямой, то тело движется прямолинейно, а если они направлены вдоль пересекающихся прямых, то тело движется криволинейно.
Верно и обратное утверждение: если тело движется криволинейно, то это означает, что на него действует какая-то сила, меняющая направление скорости, причем в каждой точке сила и скорость направлены вдоль пересекающихся прямых.

Движение тела по окружности с постоянной по модулю скоростью

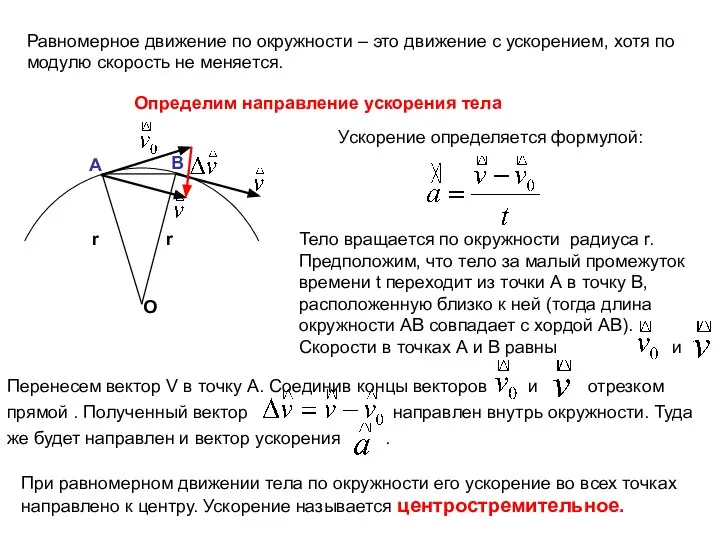
Равномерное движение по окружности – это движение с ускорением, хотя по модулю скорость не меняется.
Определим направление ускорения тела
Ускорение определяется формулой:
Тело вращается по окружности радиуса r. Предположим, что тело за малый промежуток времени t переходит из точки А в точку В, расположенную близко к ней (тогда длина окружности АВ совпадает с хордой АВ). Скорости в точках А и В равны и
Перенесем вектор V в точку А. Соединив концы векторов и отрезком прямой . Полученный вектор направлен внутрь окружности. Туда же будет направлен и вектор ускорения .
При равномерном движении тела по окружности его ускорение во всех точках направлено к центру. Ускорение называется центростремительное.

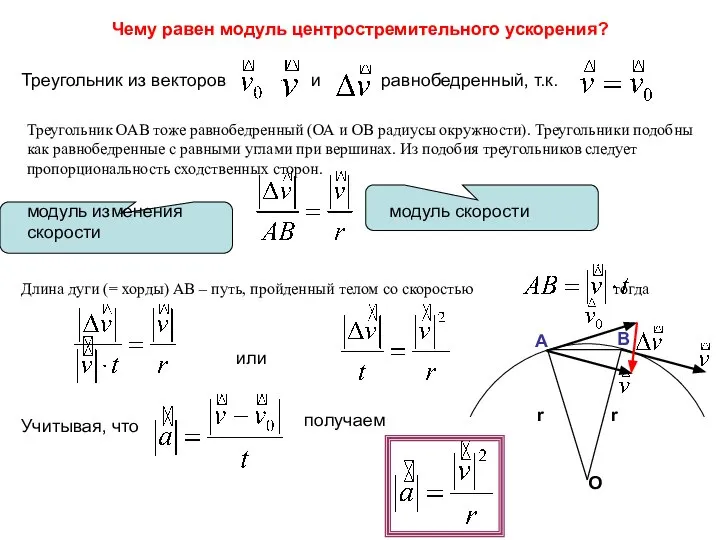
Чему равен модуль центростремительного ускорения?
Треугольник из векторов и равнобедренный, т.к.
Треугольник ОАВ тоже равнобедренный (ОА и ОВ радиусы окружности). Треугольники подобны как равнобедренные с равными углами при вершинах. Из подобия треугольников следует пропорциональность сходственных сторон.
модуль скорости
модуль изменения скорости
Длина дуги (= хорды) АВ – путь, пройденный телом со скоростью тогда
или
Учитывая, что
получаем

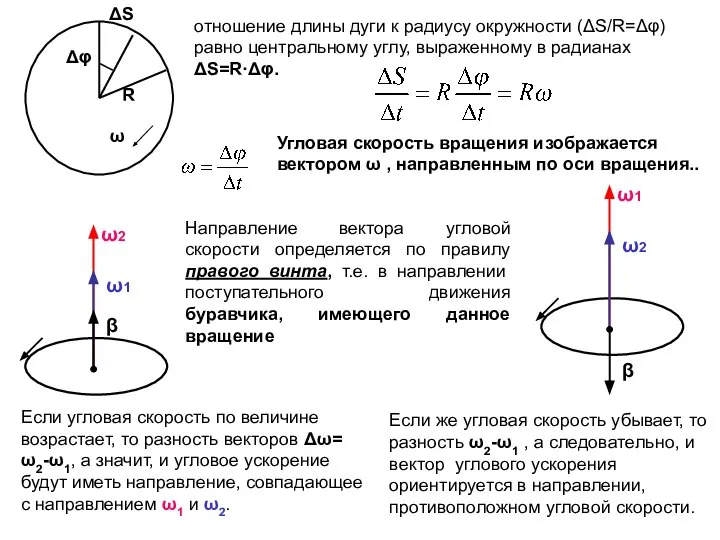
отношение длины дуги к радиусу окружности (ΔS/R=Δφ) равно центральному углу, выраженному в радианах ΔS=R·Δφ.
Угловая скорость вращения изображается вектором ω , направленным по оси вращения..
Направление вектора угловой скорости определяется по правилу правого винта, т.е. в направлении поступательного движения буравчика, имеющего данное вращение
Если угловая скорость по величине возрастает, то разность векторов Δω= ω2-ω1, а значит, и угловое ускорение будут иметь направление, совпадающее с направлением ω1 и ω2.
Если же угловая скорость убывает, то разность ω2-ω1 , а следовательно, и вектор углового ускорения ориентируется в направлении, противоположном угловой скорости.

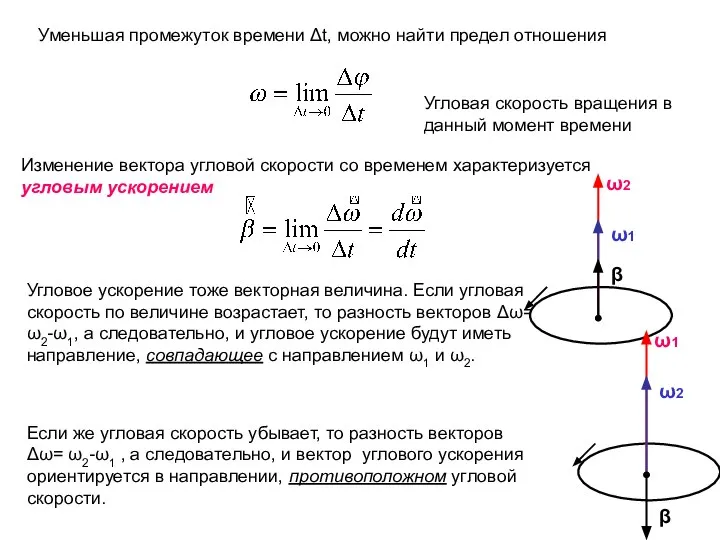
Угловое ускорение тоже векторная величина. Если угловая скорость по величине возрастает, то разность векторов Δω= ω2-ω1, а следовательно, и угловое ускорение будут иметь направление, совпадающее с направлением ω1 и ω2.
Если же угловая скорость убывает, то разность векторов Δω= ω2-ω1 , а следовательно, и вектор углового ускорения ориентируется в направлении, противоположном угловой скорости.
Уменьшая промежуток времени Δt, можно найти предел отношения
Угловая скорость вращения в данный момент времени
Изменение вектора угловой скорости со временем характеризуется угловым ускорением

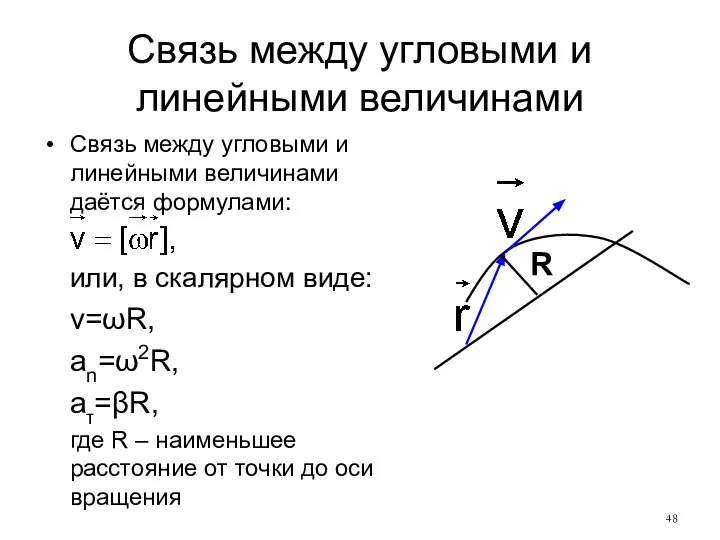
Связь между угловыми и линейными величинами
Связь между угловыми и линейными величинами даётся формулами:
или, в скалярном виде:
v=ωR,
an=ω2R,
aτ=βR,
где R – наименьшее расстояние от точки до оси вращения
R

Период обращения
Движение тела по окружности часто характеризуют не скоростью , а промежутком времени, за который тело совершает один полный оборот.
Эта величина называется периодом обращения Т.
Единица измерения – 1с (секунда)
Если известен период обращения Т, то легко найти и скорость движения тела по окружности.
За время, равное периоду Т, тело проходит путь, равный длине окружности 2πr. Тогда
радиус окружности
Подставив это выражение в формулу ускорения, получаем еще одно выражение для центростремительного ускорения

Частота обращения
Движение точки по окружности можно характеризовать числом оборотов по окружности в единицу времени
Эта величина называется частота обращения n
С периодом обращения она связана обратной зависимостью.
Единица измерения 1/с , или с-1
Скорость движения тела по окружности можно выразить и через частоту n. При одном обороте тело проходит путь 2πr. Тогда при n оборотах тело за 1с пройдет путь 2πrn.
Подставим это выражение в формулу для ускорения

В зависимости от тангенциальных и нормальных составляющих ускорения виды движений делятся на :