Содержание
- 2. Прямая задача
- 3. Формулировка обратной задачи
- 4. Для решения обратной задачи получим следующее интегральное уравнение:
- 7. Численный метод решения обратных задач
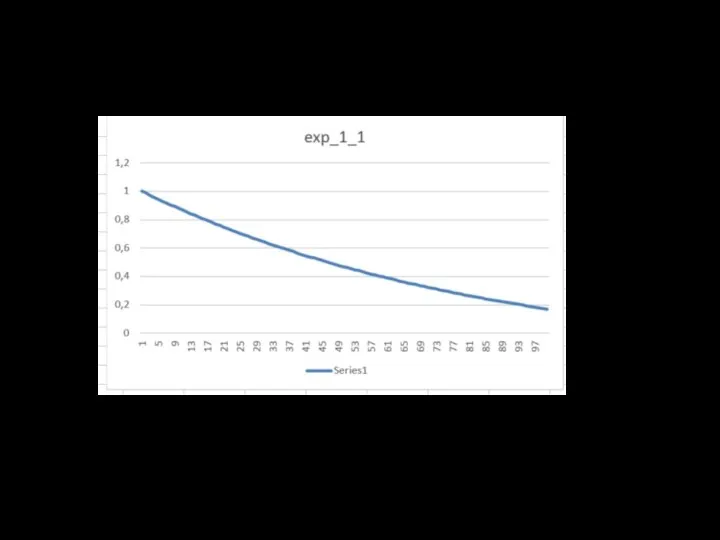
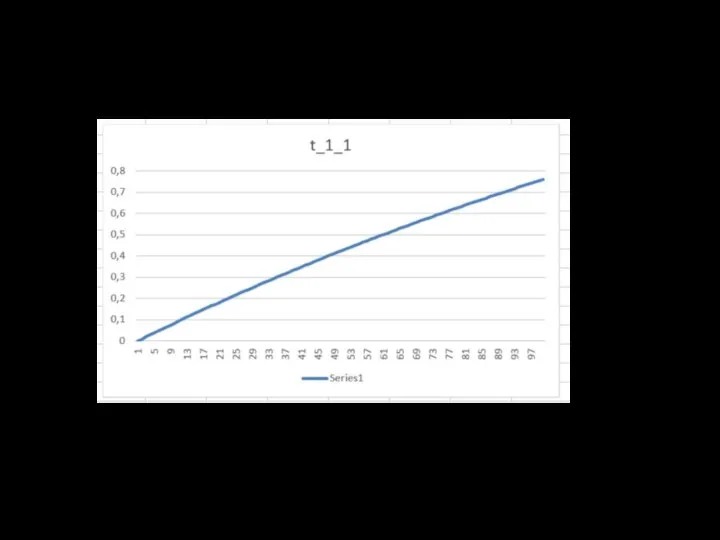
- 8. Результаты расчётов f (x) = sin πx, g(t) = e −t
- 9. Результаты расчётов f (x) = cos πx g(t) = e −t
- 10. Результаты расчётов f (x) = 1 + cos 2πx g(t) = t
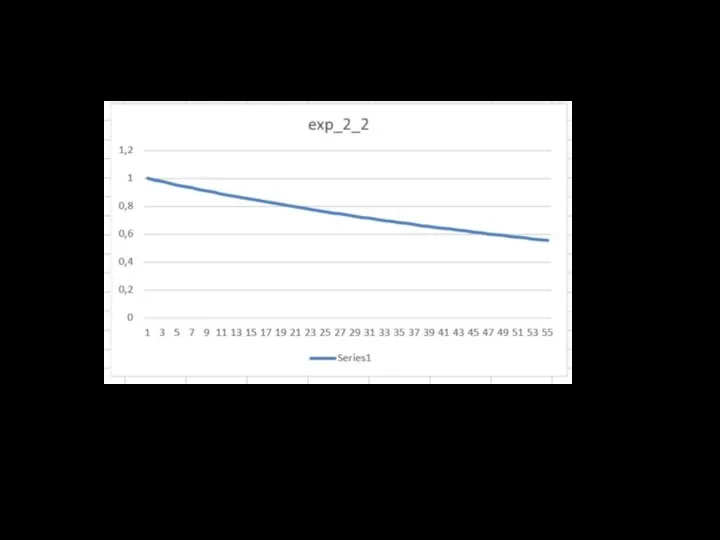
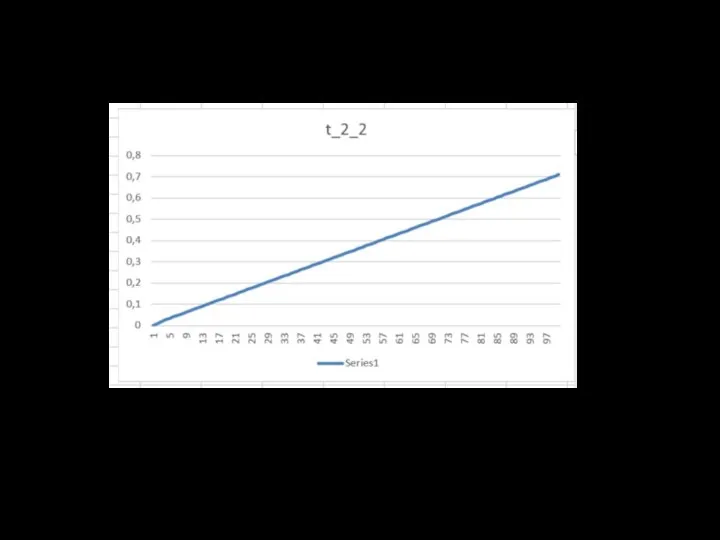
- 11. Результаты расчётов f (x) = sin πx g(t) = t
- 13. Скачать презентацию






 Наблюдение сплошного и линейчатых спектров
Наблюдение сплошного и линейчатых спектров Решение задач по теме Закон всемирного тяготения
Решение задач по теме Закон всемирного тяготения Судовые двигатели внутреннего сгорания. Лекция 11
Судовые двигатели внутреннего сгорания. Лекция 11 Сила трения
Сила трения Тепловые состояния. Макро и микропараметры теплового равновесия
Тепловые состояния. Макро и микропараметры теплового равновесия Уравновешенность и уравновешивание двигателей. Лекция №6-7
Уравновешенность и уравновешивание двигателей. Лекция №6-7 Сила Архимеда – выталкивающая сила
Сила Архимеда – выталкивающая сила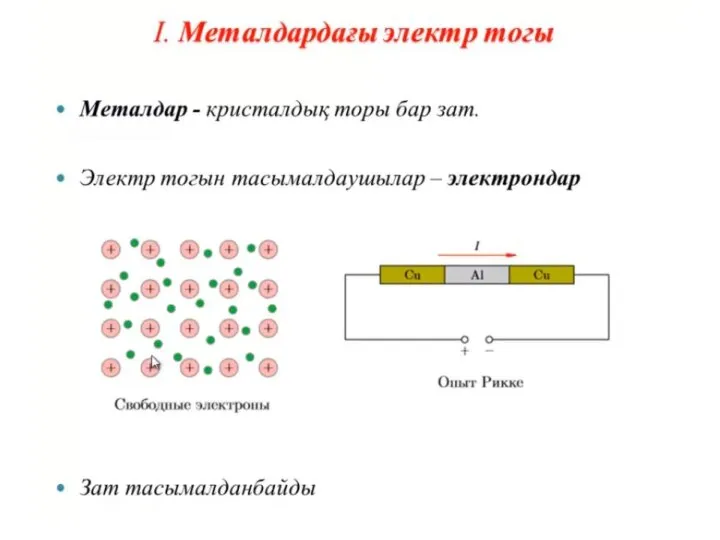 Әр түрлі ортадағы
Әр түрлі ортадағы Оптичні ілюзії
Оптичні ілюзії Характеристики волнового движения
Характеристики волнового движения Переходные процессы в электроэнергетических системах
Переходные процессы в электроэнергетических системах Найдем правильную дорогу
Найдем правильную дорогу Klassifikatsia_dvigateley_vnutrennego_sgorania
Klassifikatsia_dvigateley_vnutrennego_sgorania Строение вещества, атома
Строение вещества, атома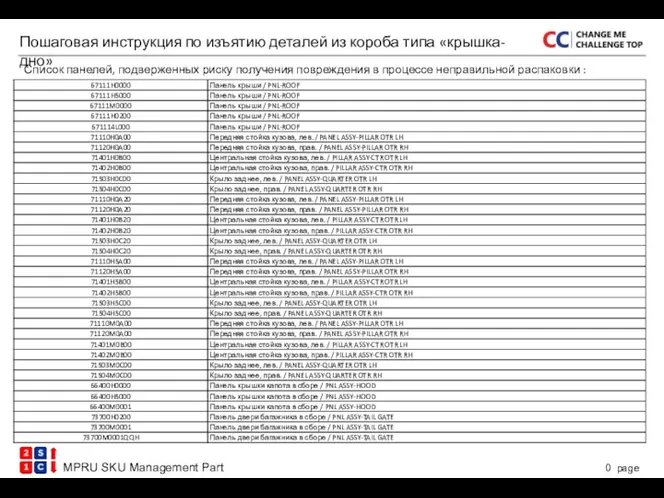 Пошаговая инструкция по изъятию деталей из короба типа крышка-дно
Пошаговая инструкция по изъятию деталей из короба типа крышка-дно Метрология. Погрешности измерений
Метрология. Погрешности измерений Что изучает физика. Основные источники физических знаний
Что изучает физика. Основные источники физических знаний Атом (по Демокриту) – простейшая, неделимая далее частица
Атом (по Демокриту) – простейшая, неделимая далее частица Презентация на тему История открытия радиоактивности
Презентация на тему История открытия радиоактивности  Алгоритмизация информации на уроках физики
Алгоритмизация информации на уроках физики Молярная масса
Молярная масса Графен – бұл кәдімгі алмаз бен графиттен
Графен – бұл кәдімгі алмаз бен графиттен Радиоактивные изотопы в биологии и медицине, археологии
Радиоактивные изотопы в биологии и медицине, археологии Переносное зарядное устройство
Переносное зарядное устройство Задачи на работу
Задачи на работу Электростатика
Электростатика Презентация на тему Кинетическая и потенциальная энергия
Презентация на тему Кинетическая и потенциальная энергия  Свердління отворів. Оброблення країв виробів
Свердління отворів. Оброблення країв виробів