Содержание
- 2. ВИДЕОРОЛИК Вращение
- 3. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ – движение криволинейное, так как траекторией является окружность. – движение равномерное, так как
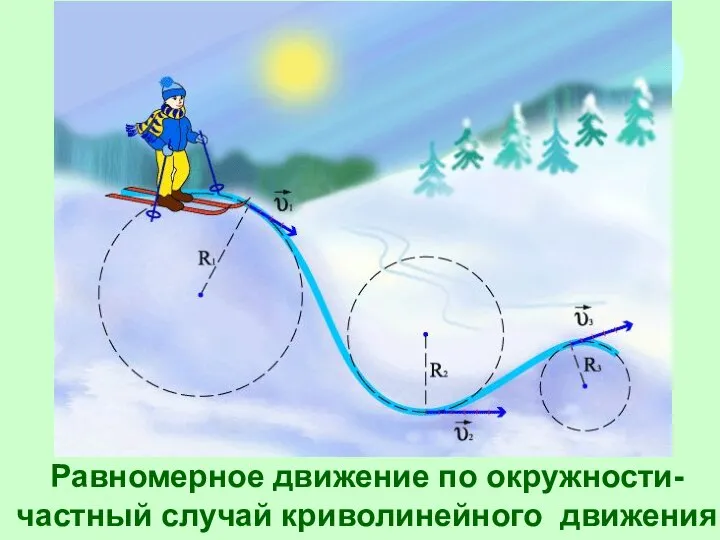
- 4. Равномерное движение по окружности- частный случай криволинейного движения
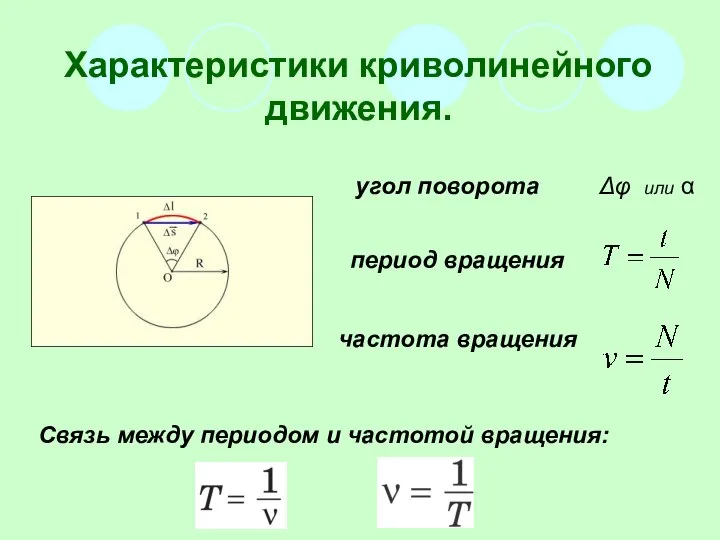
- 6. угол поворота Δφ или α период вращения частота вращения Характеристики криволинейного движения. Связь между периодом и
- 7. Скорость движения. угловая скорость линейная скорость
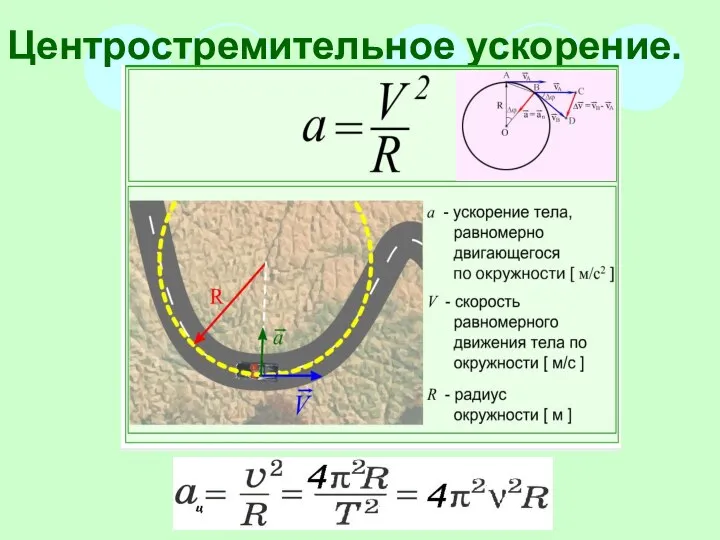
- 8. Центростремительное ускорение.
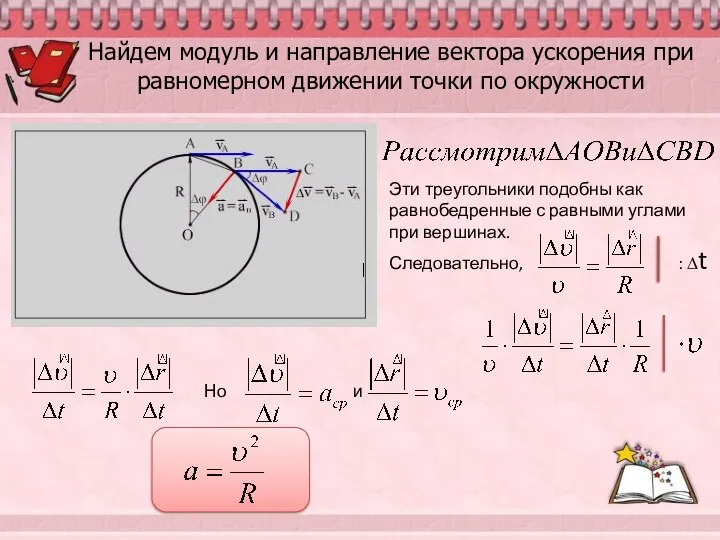
- 9. Найдем модуль и направление вектора ускорения при равномерном движении точки по окружности Эти треугольники подобны как
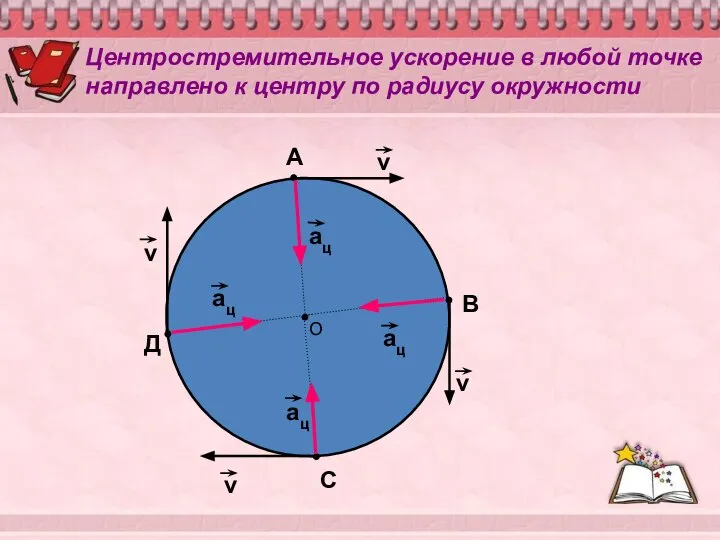
- 10. О А В С Д ац ац ац ац Центростремительное ускорение в любой точке направлено к
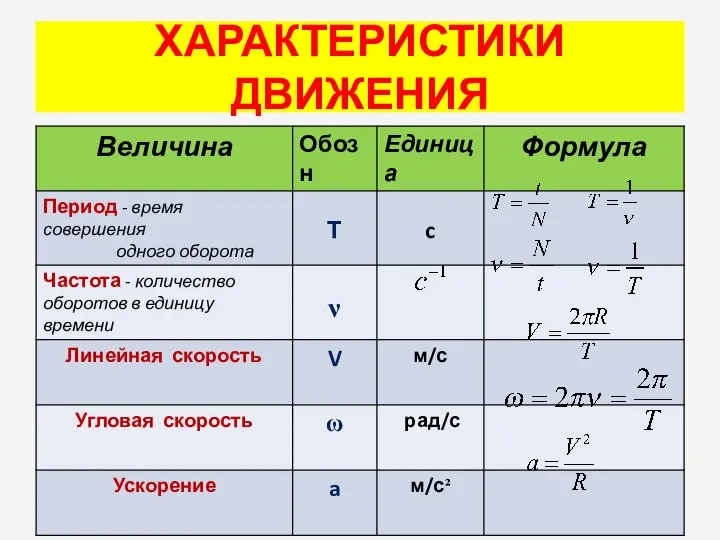
- 11. ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ
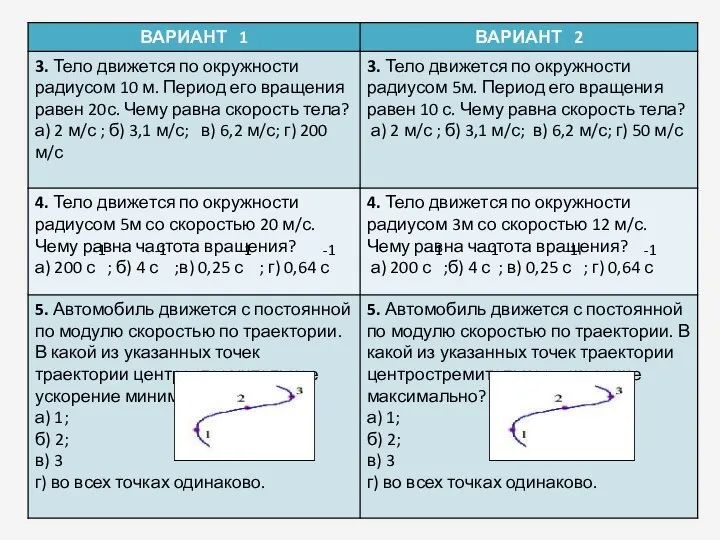
- 12. Шар, вращающийся на нити длиной 80см, совершил за одну минуту 150 оборотов. Определить все параметры вращательного
- 13. ВОПРОСЫ 1. Как направлен вектор скорости? 2. Как направлен вектор ускорения? 3. Какой угол между скоростью
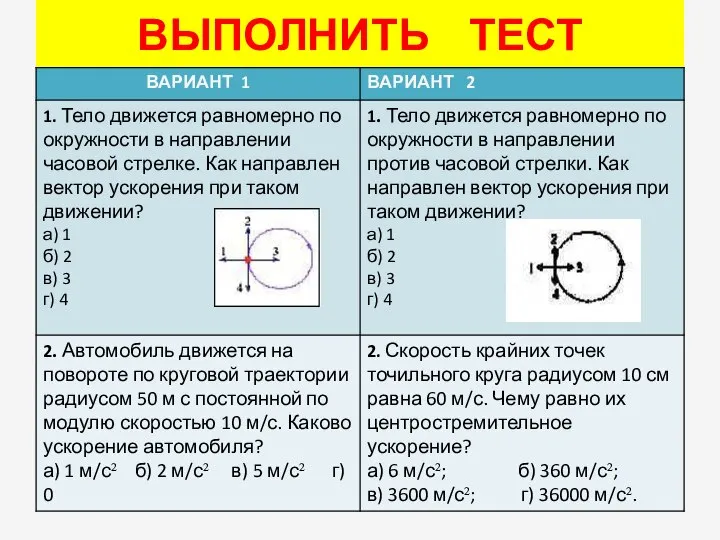
- 14. ВЫПОЛНИТЬ ТЕСТ
- 15. -1 -1 -1 -1 -1 -1 -1 -1
- 17. Скачать презентацию





 Затухающие и вынужденные колебания. Дифференциальное уравнение колебаний. Явление резонанса
Затухающие и вынужденные колебания. Дифференциальное уравнение колебаний. Явление резонанса Гамма-излучение. (Тема 1.5)
Гамма-излучение. (Тема 1.5) Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1
Идентификация и моделирование CW–crds спектра поглощения молекулы двуокиси азота в области 6000 – 6400 см -1 Молекулярная физика. Ученые и их открытия
Молекулярная физика. Ученые и их открытия Расчет шатуна. Лекция №11а
Расчет шатуна. Лекция №11а Презентация на тему Закон всемирного тяготения
Презентация на тему Закон всемирного тяготения  Термодинамические процессы
Термодинамические процессы Классификация магнитных материалов специального назначения. (Лекция 8)
Классификация магнитных материалов специального назначения. (Лекция 8) Устройство и работа ДВС (двигателя внутреннего сгорания)
Устройство и работа ДВС (двигателя внутреннего сгорания) Динамика
Динамика Презентация на тему Радиоактивные превращения атомных ядер (9 класс)
Презентация на тему Радиоактивные превращения атомных ядер (9 класс)  Уравнение состояния идеального газа. Газовые законы
Уравнение состояния идеального газа. Газовые законы Основы аэродинамики
Основы аэродинамики Презентация на тему Внутренняя энергия. Способы изменения внутренней энергии
Презентация на тему Внутренняя энергия. Способы изменения внутренней энергии  Антони ван Левенгук. Изобретатель микроскопа
Антони ван Левенгук. Изобретатель микроскопа Законы природы, проявления законов
Законы природы, проявления законов Ядерные силы. Энергия связи частиц в ядре. Деление ядер урана. Цепная реакция
Ядерные силы. Энергия связи частиц в ядре. Деление ядер урана. Цепная реакция Презентация на тему Техника безопасности на уроках физики
Презентация на тему Техника безопасности на уроках физики  Определение удельной плотности и температуры растворов
Определение удельной плотности и температуры растворов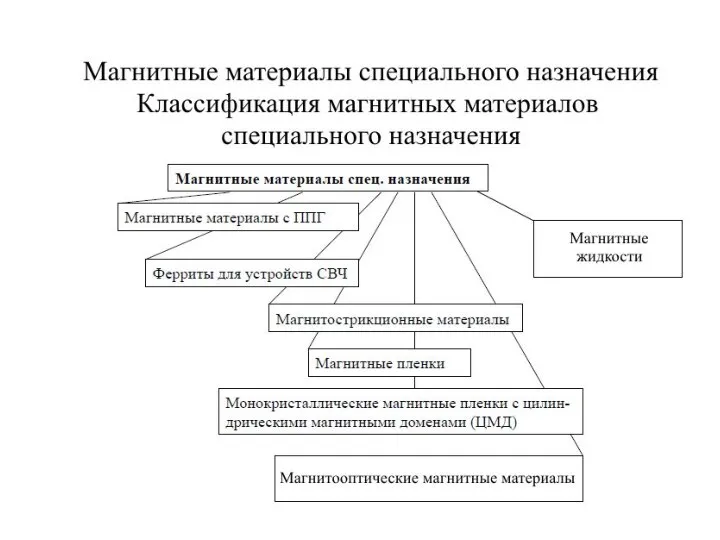 Магнитные материалы специального назначения. (Лекция 8)
Магнитные материалы специального назначения. (Лекция 8) Плоский механизм. Задача 4
Плоский механизм. Задача 4 Фотоно-кристалличские волокна
Фотоно-кристалличские волокна Условия, при которых тело плавает и при которых тонет
Условия, при которых тело плавает и при которых тонет Понятие о газах
Понятие о газах Сборка механического манипулятора
Сборка механического манипулятора Использование теплового действия электрического тока в устройстве теплиц и инкубаторов
Использование теплового действия электрического тока в устройстве теплиц и инкубаторов Механические волны: процесс распространения механических колебаний в пространстве
Механические волны: процесс распространения механических колебаний в пространстве Лестница знаний
Лестница знаний