Слайд 2Джеймс Клерк (Кларк) Максвелл
Британский физик и математик. Шотландец по происхождению. Член

Лондонского королевского общества (1861). Он является пионером количественной теории цветов, автором принципа цветной фотографии
Слайд 3Теория цветов Максвелла
В экспериментах по смешиванию цветов, во многом независимо повторявших опыты

Германа Гельмгольца, Максвелл применил "цветовой волчок", диск которого был разделён на окрашенные в разные цвета секторы, а также "цветовой ящик", разработанную им самим оптическую систему, позволявшую смешивать эталонные цвета.
Слайд 4Максвелл представил свою "Теорию цветного зрения", признанную основательницей количественного цветового измерения (колориметрии).
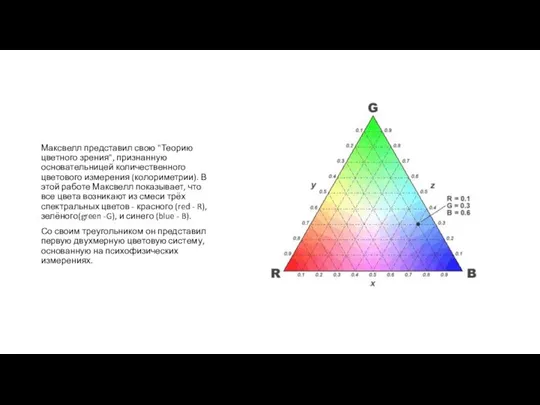
В этой работе Максвелл показывает, что все цвета возникают из смеси трёх спектральных цветов - красного (red - R), зелёного(green -G), и синего (blue - B).
Со своим треугольником он представил первую двухмерную цветовую систему, основанную на психофизических измерениях.
Слайд 5r = R/(R+G+B), g = G/(R+G+B), and b = B/(R+G+B). Эти новые
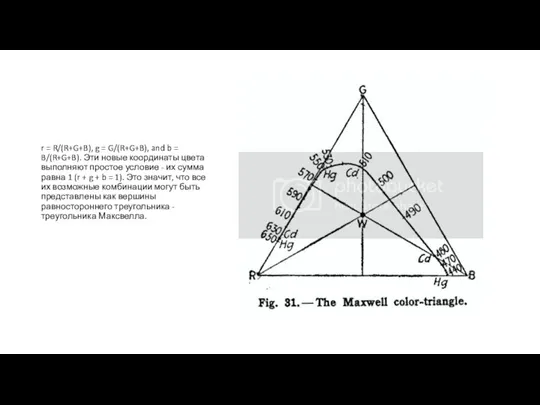
координаты цвета выполняют простое условие - их сумма равна 1 (r + g + b = 1). Это значит, что все их возможные комбинации могут быть представлены как вершины равностороннего треугольника - треугольника Максвелла.




 Швейная машина. История и устройсво
Швейная машина. История и устройсво Инструменты, механизмы и технические устройства
Инструменты, механизмы и технические устройства Аномальність фізичних властивостей води
Аномальність фізичних властивостей води Законы постоянного тока
Законы постоянного тока Презентация на тему Строение вещества
Презентация на тему Строение вещества  Формульный диктант Кинематика, законы Ньютона, сохранения, статика
Формульный диктант Кинематика, законы Ньютона, сохранения, статика Механика. Повторение. Занятие 7
Механика. Повторение. Занятие 7 Машиноведение
Машиноведение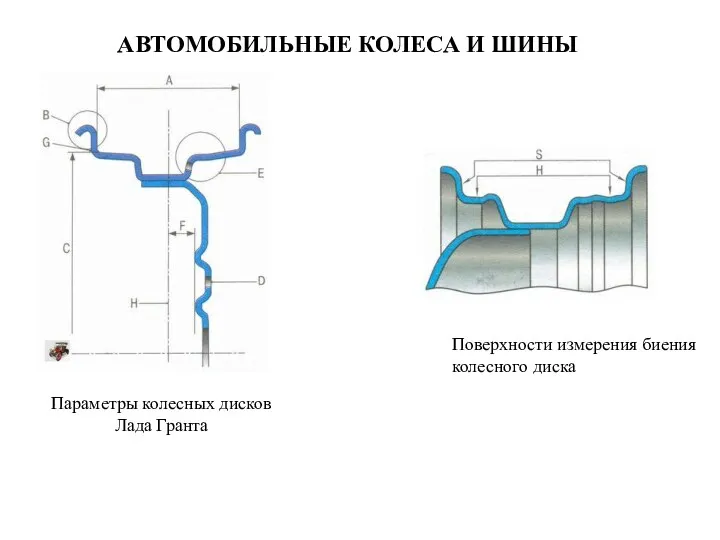 Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта
Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта Инновационная концепция электронного корабля
Инновационная концепция электронного корабля Решение задач по теме Тепловые явления. Агрегатные состояния вещества
Решение задач по теме Тепловые явления. Агрегатные состояния вещества Электрическое поле. Лекция № 1
Электрическое поле. Лекция № 1 Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al
Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al Теория деформаций. Практическое занятие
Теория деформаций. Практическое занятие Сцепление. Тесты к теоретическим занятиям
Сцепление. Тесты к теоретическим занятиям Сила трения. Опыт №1. Наблюдение явления трения
Сила трения. Опыт №1. Наблюдение явления трения Презентация на тему КПД тепловых двигателей (8 класс)
Презентация на тему КПД тепловых двигателей (8 класс)  Акустичне явище грім
Акустичне явище грім Механика и элементы специальной теории относительности
Механика и элементы специальной теории относительности Бионика. Аэродинамические прототипы
Бионика. Аэродинамические прототипы давл жидк
давл жидк Электризация. Взаимодействие заряженных тел
Электризация. Взаимодействие заряженных тел Цепь переменного тока с индуктивностью
Цепь переменного тока с индуктивностью Машины и механизмы
Машины и механизмы Общие принципы инженерных расчетов
Общие принципы инженерных расчетов Škoda Octavia. Кузов. Оборудование кузова
Škoda Octavia. Кузов. Оборудование кузова Драйвер двигателя постоянного тока. Вспомогательные функции
Драйвер двигателя постоянного тока. Вспомогательные функции Викторина по физике
Викторина по физике